Compressive Sensing
Introduction
Compressed Sensing (CS) is a novel sensing/sampling paradigm that allows the recovery of sparse (few nonzeros) or compressible (quickly decaying entries) signals from far fewer measurments than the Nyquist rate. The sparsity assumption is easily realized in practice, as, for instance, natural images are sparse in the Wavelet domain (e.g. JPEG2000 compression) and seismic images are well represented in terms of curvelets. (Candes et al., 2006) and (D. Donoho, 2006) first provided rigorous theory underlining under which conditions a sparse signal could be recovered from subsampled measurements.
Sparse recovery
Let a high-dimensional signal \(x \in \mathbb{R}^N\) be \(k\)-sparse, i.e., \(\|x\|_0 \leq k\), where \(\|x\|_0\) denotes the number of non-zero entries of the vector \(x\). The goal is to recover \(x\) from non-adaptive linear measurments \(y = {\Psi} x\), where \(\Psi\) is an appropriate \(n \times N\) measurment matrix. Clearly, we can recover all \(x \in \mathbb{R}^N\) exactly if \(n \geq N\) and \(\Psi\) has full rank. On the other hand, if \(n < N\), i.e., the number of measurments is less than the ambient dimension, the system \(y = {\Psi} x\) has infinitely many solutions, rendering it generally impossible to recover \(x\) from \(y\) uniquely. CS handles this scenario by using prior information that \(x\) is sparse (or compressible) to recover the original signal. In particular, we look for, among all vectors \(x\) that match the data, i.e. \(Ax = b\), the solution \(x^*\) with the smallest number of non-zero entries, i.e., solve the optimization problem \[ \begin{equation*} \underset{x}{\text{minimize}} \quad \|z\|_0 \quad \text{subject to} \quad y = {\Psi} z. \end{equation*} \] It can be shown that if every \(n\text{-by-}n\) submatrix of \(\Psi\) is nonsingular, then \(x^* = x\), i.e., (1) recovers every \(k\)-sparse \(x\) exactly whenever \(k < n/2\), e.g., see (D. L. Donoho and Elad, 2003). In other words, to acquire a \(k\)- sparse signal, we only need to obtain \(n > 2k\) measurements regardless of the ambient dimension N and solve the optimization problem (1). Unfortunately, this observation is not very useful in practice because the program (1) is NP- hard (Natarajan, 1995) and sensitive to the sparsity assumption and additive noise. The major breakthrough in CS has been to specify explicit conditions under which the minimizer of (1) also solves its convex relaxation, \[ \begin{equation*} \underset{x}{\text{minimize}} \quad \|z\|_1 \quad \text{subject to} \quad y = {\Psi} z, \end{equation*} \] which is computationally tractable. Specifically, these conditions (Candes et al., 2006; D. Donoho, 2006) determine what measurement matrices \(\Psi\) can be used so that (2) is guaranteed to recover all \(k\)-sparse \(x \in \mathbb{R}^N\) from \(n\) measurements given by \(y = {\Psi}x\). In words, the main requirement is that \(\Psi\) nearly preserves the length of all sparse vectors.
Compressive sensing for seismic signals
According to CS, successful dimensionality reduction hinges on an incoherent sampling strategy where coherent aliases are turned into relatively harmless white Gaussian noise. The challenges of adapting this approach to real-life problems in exploration seismology are threefold as projected by (Herrmann et al., 2012). First, seismic data acquisition is subject to physical constraints on the placement, type, and number of (possibly simultaneous) sources, and numbers of receivers. These constraints in conjunction with the extremely large size of seismic data calls for approaches specific to the seismic case. Second, while CS offers significant opportunities for dimensionality reduction, there remain still challenges in adapting the scientific-computing workflow to this new approach, and again, CS offers an opportunity to make computation much more efficient. Third, seismic wavefields are highly multiscale, multidirectional, and are the solution of the wave equation. This calls for the use of directional and anisotropic transforms, e.g., curvelets.
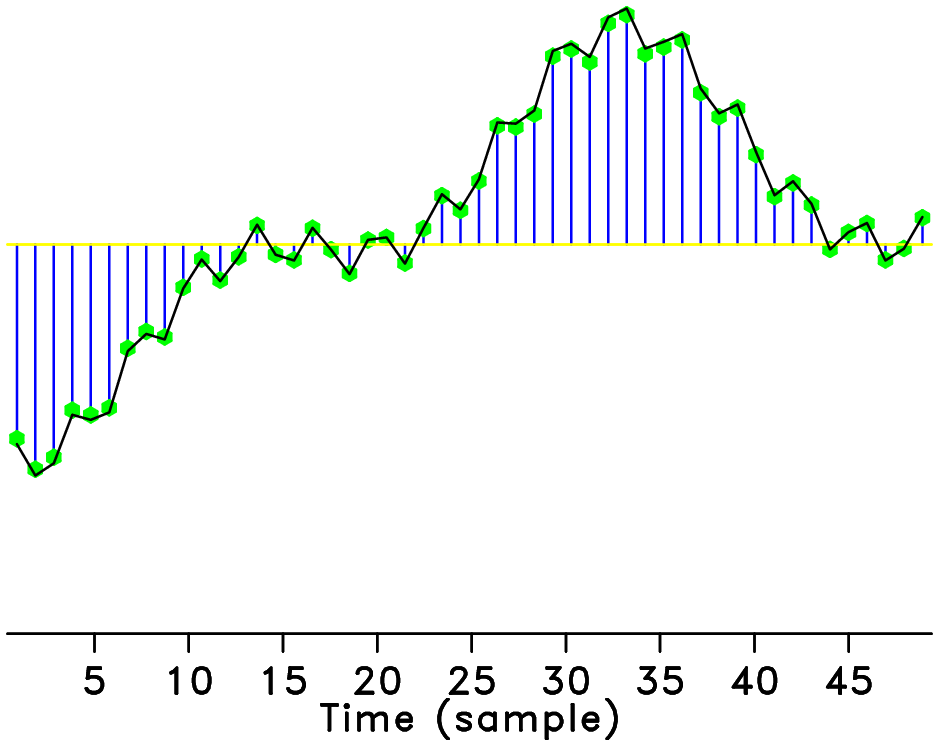
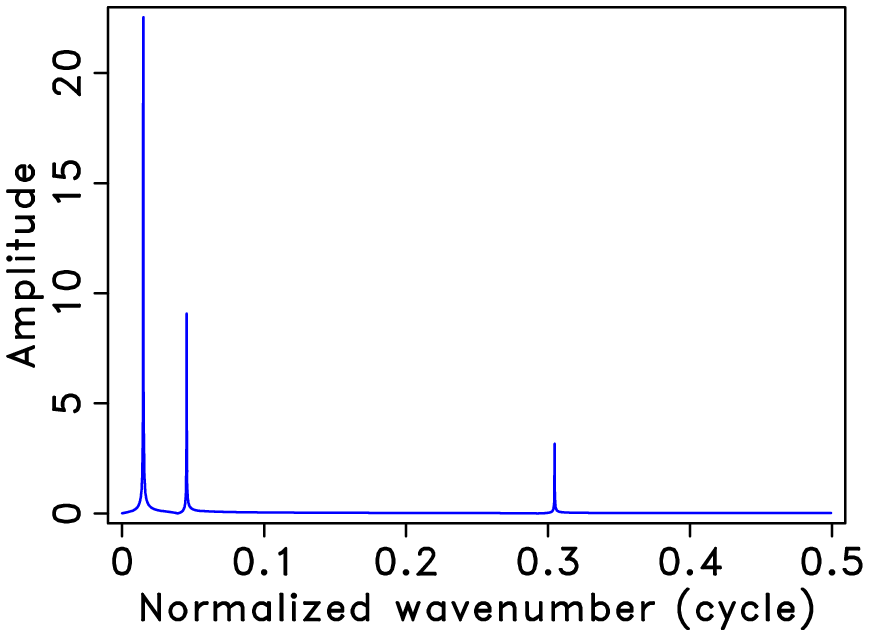
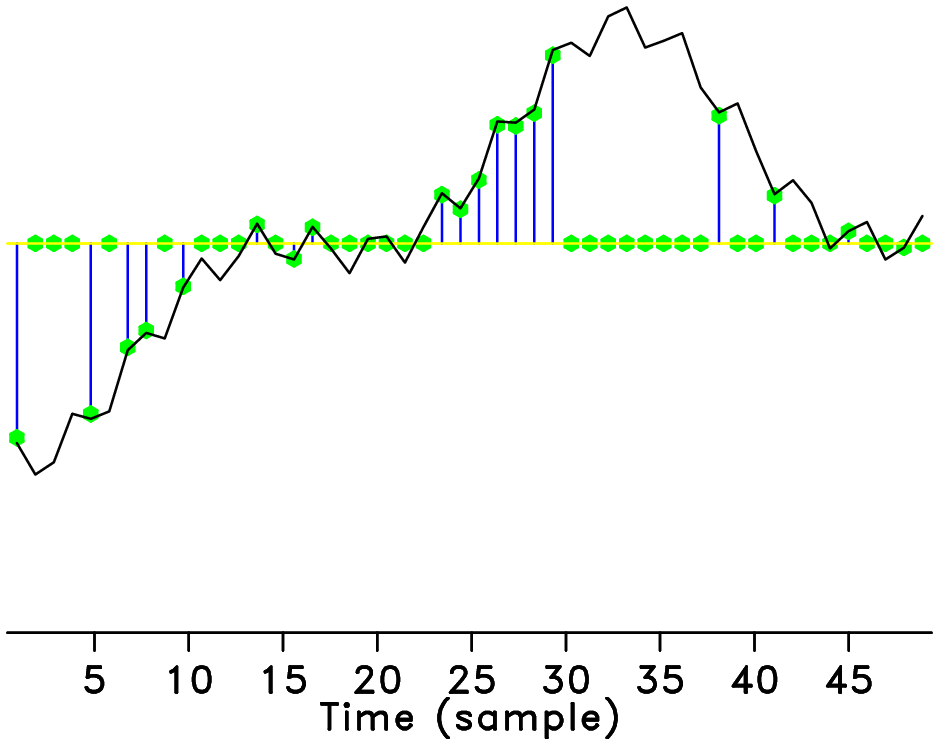
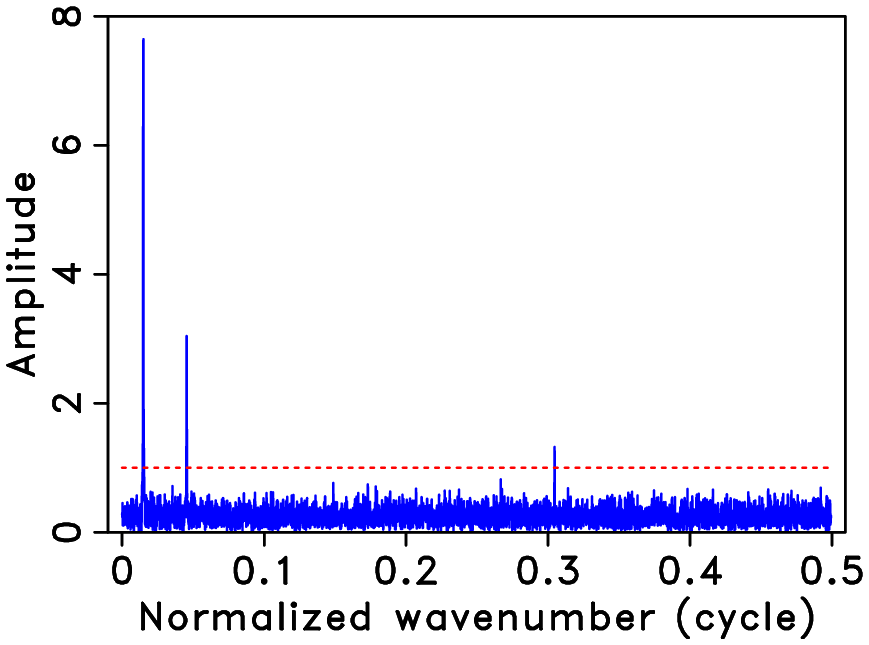
Applications
In this group, we explore the ideas of compressive sensing to tackle the difficulties related to seismic data starting from acquisition upto full-waveform inversion. In every aspects of seismic data, we have demonstrated that in leveraging the ideas from the field of compressive sensing, we reap immense benefits via exploiting the sparse structure of seismic data in a variety of applications.
Acquisition
(Software overview available here)
Seismic data acquisition in marine environments is a costly process that calls for the adoption of simultaneous-source or randomized acquisition - an emerging technology that is stimulating both geophysical research and commercial efforts. Simultaneous marine acquisition calls for the development of a new set of design principles and post-processing tools. In this group, we explore the properties of a specific class of randomized simultaneous acquisition matrices and demonstrate that sparsity-promoting recovery improves the quality of reconstructed seismic data volumes. We propose a practical randomized marine acquisition scheme wherein the sequential sources fire airguns at only randomly time-dithered instances, reducing the overall time needed to shoot a survey while simultaneously injecting sufficient randomness in to the acquisition in order to recover the original data. We demonstrate that the recovery using sparse approximation from random time-dithering with a single source approaches the recovery from simultaneous-source acquisition with multiple sources (Mansour et al., 2012; Wason and Herrmann, 2013).
Seismic data reconstruction and denoising
(Software overview available here)
Seismic data recovery from data with missing traces on otherwise regular acquisition grids forms a crucial step in the seismic processing flow. For instance, unsuccessful recovery leads to imaging artifacts and to erroneous predictions for the multiples, adversely affecting the performance of multiple elimination. We have proposed a non-parametric transform-based recovery method that exploits the compression of seismic data volumes by recently developed curvelet frames. The elements of this transform are multidimensional, directional, and locally resemble wavefronts present in the data, which leads to a compressible representation for seismic data. This compression enables us to directly apply curvelet-based based on \(\ell 1\) minimization to seismic data recovery (Hennenfent and Herrmann, 2008; Herrmann and Hennenfent, 2008; Mansour et al., 2013).
Estimation of primaries by sparse inversion
(Software overview available here)
Estimation of primaries by sparse inversion (EPSI) avoids the need for adaptive subtraction of approximate multiple predictions by directly inverting for the multiple-free subsurface impulse response as a collection of band-limited spikes. Although it can be shown that the correct primary impulse response is obtained through the sparsest possible solution, the original EPSI algorithm was not designed to take advantage of this result, and instead it relies on a multitude of inversion parameters, such as the level of sparsity per gradient update. We proposed and tested a new algorithm, named robust EPSI, in which we make obtaining the sparsest solution an explicit goal and thereby reducing the number of parameters that need to be tuned. Our approach remains a gradient-based approach like the original algorithm, but it is derived from a new biconvex optimization framework based on an extended basis-pursuit denoising formulation. Furthermore, because it is based on a general framework, robust EPSI can recover the impulse response in transform domains, such as sparsifying curvelet-based representations, without changing the underlying algorithm. We found that the sparsity-minimizing objective of our formulation enabled it to operate successfully on a variety of synthetic and field marine data sets without excessive tweaking of inversion parameters. We also found that recovering the solution in alternate sparsity domains can significantly improve the quality of the directly estimated primaries, especially for weaker late-arrival events. In addition, we found that robust EPSI produces a more artifact-free impulse response compared to the original algorithm (Lin and Herrmann, 2013).
Sparsity promoting based Least-Square Migration
(Software overview available here)
Seismic imaging is a linearized inversion problem relying on the minimization of a least-squares misfit functional as a function of the medium perturbation. The success of this procedure hinges on our ability to handle large systems of equations–-whose size grows exponentially with the demand for higher resolution images in more and more complicated areas–-and our ability to invert these systems given a limited amount of computational resources. To overcome this “curse of dimensionality” in problem size and computational complexity, we propose a combination of randomized dimensionality-reduction and divide-and-conquer techniques by exploiting both the sparsity of the model perturbation in curvelets as well as the source linearity in the wave equation. This approach allows us to take advantage of sophisticated sparsity-promoting solvers that work on a series of smaller subproblems each involving a small randomized subset of data. These subsets correspond to artificial simultaneous-source experiments made of random superpositions of sequential-source experiments. By changing these subsets after each subproblem is solved, we are able to attain an inversion quality that is competitive while requiring fewer computational, and possibly, fewer acquisition resources (Herrmann and Li, 2012).
Fast Imaging with Surface-related multiples
(Software overview available here)
In marine exploration seismology, surface-related multiples are usually treated as noise mainly because subsequent processing steps, such as migration-velocity analysis and imaging, require multiple-free data. Failure to remove these wavefield components from the data may lead to erroneous estimates for migration velocity or result in strong coherent artifacts that interfere with the imaged reflectors. On the other hand, multiples interact with the free surface and are therefore exposed more to the subsurface. Hence, multiples carry complementary information compared to the primaries and when processed correctly improve the illumination. Given a sufficiently accurate background velocity model and an estimate for the source signature, we propose a wave-equation based inversion procedure that produces accurate images of velocity perturbations in the subsurface from the total upgoing wavefield including surface-related multiples. Because our method uses subsampling techniques, we obtain high-quality true-amplitude least-squares migrated images at computational costs of roughly a single reverse-time migration with fully sampled data. We also incur a minimal overhead from incorporating the multiples by having the wave-equation solver carry out the multiple-predictions via the inclusion of an areal source. Our method derives its efficacy from promoting curvelet-domain sparsity in the imaged domain and leads to images that are virtually free of artifacts from data that includes multiples. The method is also relatively robust with respect to linearization errors and errors in the background velocity model (Tu and Herrmann, 2014).
Full-waveform inversion
(Software overview available here)
Wave-equation based seismic inversion can be formulated as a nonlinear inverse problem where the medium properties are obtained via minimization of a least- squares misfit functional. The demand for higher resolution models in more geologically complex areas drives the need to develop techniques that explore the special structure of full-waveform inversion to reduce the computational burden and to regularize the inverse problem. We meet these goals by using ideas from compressive sensing and stochastic optimization to design a novel Gauss-Newton method, where the updates are computed from random subsets of the data via curvelet-domain sparsity promotion and can be performed at approximately the cost of one reverse time migration using all of the data. Application of this idea to a realistic synthetic shows significantly improved results compared to traditional quasi-Newton methods, which also require several passes through the entire data set. Two different subset sampling strategies are considered: randomized source encoding, and drawing sequential shots firing at random source locations from marine data with missing near and far offsets. In both cases, we obtain excellent inversion results compared to conventional methods at reduced computational costs (Herrmann et al., 2013; Li and Herrmann, 2012 Li et al., 2012 ).
References
Candes, E., Romberg, J., and Tao, T., 2006, Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information: Information Theory, IEEE Transactions on, 52, 489–509. doi:10.1109/TIT.2005.862083
Donoho, D., 2006, Compressed sensing: Information Theory, IEEE Transactions on, 52, 1289–1306. doi:10.1109/TIT.2006.871582
Donoho, D. L., and Elad, M., 2003, Optimally sparse representation in general (nonorthogonal) dictionaries via ?1 minimization: Proceedings of the National Academy of Sciences, 100, 2197–2202. doi:10.1073/pnas.0437847100
Hennenfent, G., and Herrmann, F. J., 2008, Simply denoise: wavefield reconstruction via jittered undersampling: Geophysics, 73, V19–V28. doi:10.1190/1.2841038
Herrmann, F. J., and Hennenfent, G., 2008, Non-parametric seismic data recovery with curvelet frames: Geophysical Journal International, 173, 233–248. doi:10.1111/j.1365-246X.2007.03698.x
Herrmann, F. J., and Li, X., 2012, Efficient least-squares imaging with sparsity promotion and compressive sensing: Geophysical Prospecting, 60, 696–712. doi:10.1111/j.1365-2478.2011.01041.x
Herrmann, F. J., Calvert, A. J., Hanlon, I., Javanmehri, M., Kumar, R., Leeuwen, T. van, … Wason, H., 2013, Frugal full-waveform inversion: from theory to a practical algorithm: The Leading Edge, 32, 1082–1092. doi:10.1190/tle32091082.1
Herrmann, F. J., Friedlander, M. P., and Yilmaz, O., 2012, Fighting the curse of dimensionality: compressive sensing in exploration seismology: Signal Processing Magazine, IEEE, 29, 88–100. doi:10.1109/MSP.2012.2185859
Li, X., and Herrmann, F. J., 2012, Sparsity-promoting migration accelerated by message passing: SEG technical program expanded abstracts. SEG; SEG. doi:10.1190/segam2012-1500.1
Li, X., Aravkin, A. Y., Leeuwen, T. van, and Herrmann, F. J., 2012, Fast randomized full-waveform inversion with compressive sensing: Geophysics, 77, A13–A17. doi:10.1190/geo2011-0410.1
Lin, T. T., and Herrmann, F. J., 2013, Robust estimation of primaries by sparse inversion via one-norm minimization: Geophysics, 78, R133–R150. doi:10.1190/geo2012-0097.1
Mansour, H., Herrmann, F. J., and Yilmaz, O., 2013, Improved wavefield reconstruction from randomized sampling via weighted one-norm minimization: Geophysics, 78, V193–V206. doi:10.1190/geo2012-0383.1
Mansour, H., Wason, H., Lin, T. T., and Herrmann, F. J., 2012, Randomized marine acquisition with compressive sampling matrices: Geophysical Prospecting, 60, 648–662. doi:10.1111/j.1365-2478.2012.01075.x
Natarajan, B., 1995, Sparse approximate solutions to linear systems: SIAM Journal on Computing, 24, 227–234. doi:10.1137/S0097539792240406
Tu, N., and Herrmann, F. J., 2014, Fast imaging with surface-related multiples by sparse inversion: UBC; UBC. Retrieved from https://slim.gatech.edu/Publications/Public/Journals/GeophysicalJournalInternational/2014/tu2014fis/tu2014fis.pdf
Wason, H., and Herrmann, F. J., 2013, Time-jittered ocean bottom seismic acquisition: SEG technical program expanded abstracts. doi:10.1190/segam2013-1391.1

