Seismic data processing

Seismic data processing

Our contribution in this area is mainly focused on training generative adversarial networks (GANs; Goodfellow et al., 2014) to accelerate the existing seismic data processing workflows. To this end, we developed practical workflows in which small subsets of the data are processed (or acquired) using existing seismic processing (acquisition) techniques, and then train a convolutional neural network (CNN) to process the remaining data. This workflow can be improved—both in terms of amount of needed data and accuracy of the CNN—if there are existing processed data from neighboring surveys that can be used to pretrained the CNN (Siahkoohi et al., 2019a). Before providing numerical examples, we summarize the learning framework we use to train CNNs for out data processing tasks.

Surface-related multiple removal¹

While wave-equation based techniques for removing the free surface are applied routinely, these techniques are computationally expensive and often require dense sampling. Here, we follow a different approach where a CNN is trained to carry out the joint task of surface-related multiple removal and source-receiver side deghosting.

Specifically, we consider the situation where we have access to pairs of shot records from a neighboring survey before and after removal of the free-surface effects (surface related multiples and ghost) through standard processing. These pairs of unprocessed and processed data allow us to pretrain our CNN. To mimic this realistic scenario, we simulate pairs of shot records with and without a free surface for nearby velocity models that differ by \(25\%\) in water depth. These pairs, which correspond to changes in water depth by \(50\) \(\mathrm{m}\), are used to pretrain our network. We make this choice for demonstration purposes only, other more realistic choices are possible. Because the water depth between the nearby and current surveys differ by \(25\%\), we finetune our CNN on only \(5\%\) of unprocessed/processed shot records from the current survey—i.e., we only process a fraction of the data. We numerically simulate this scenario by generating shot records in the true model (correct water depth) with and without a free surface. While this additional training round requires extra processing, we argue that we actually reduce the computational costs by as much as \(95\%\) if we ignore the time it takes to apply our neural network and the time it takes to pretrain our network on training pairs from nearby surveys.

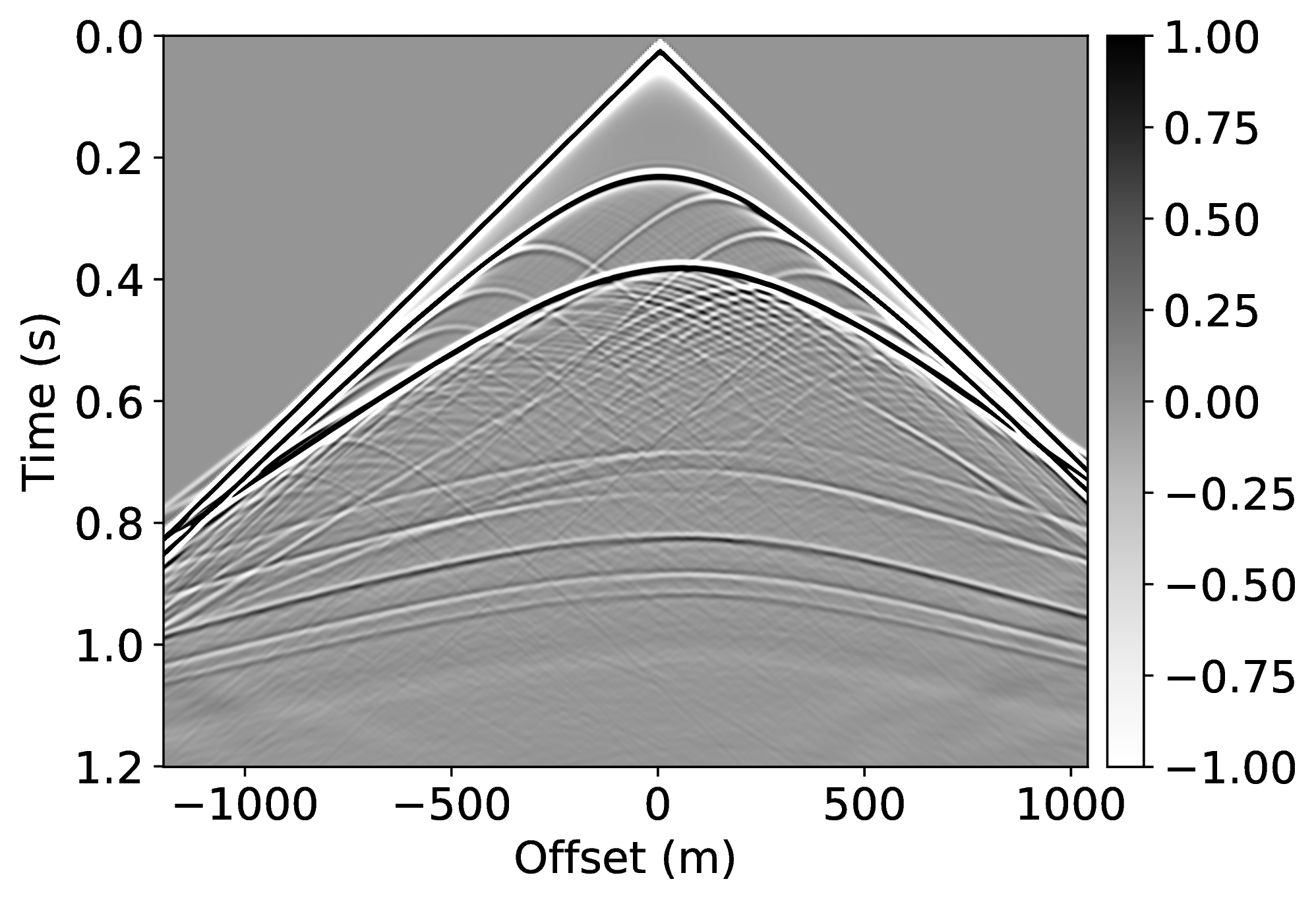
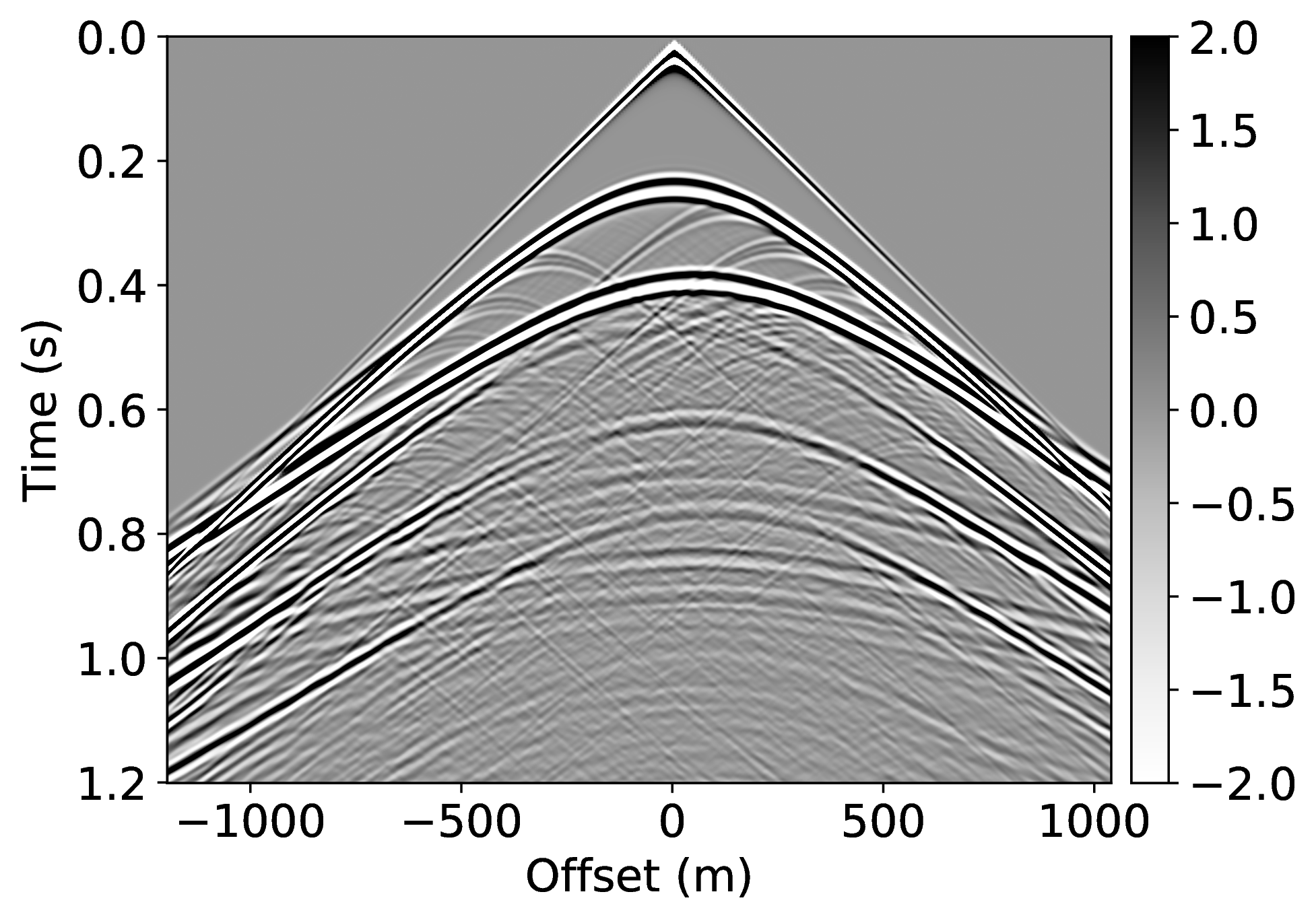
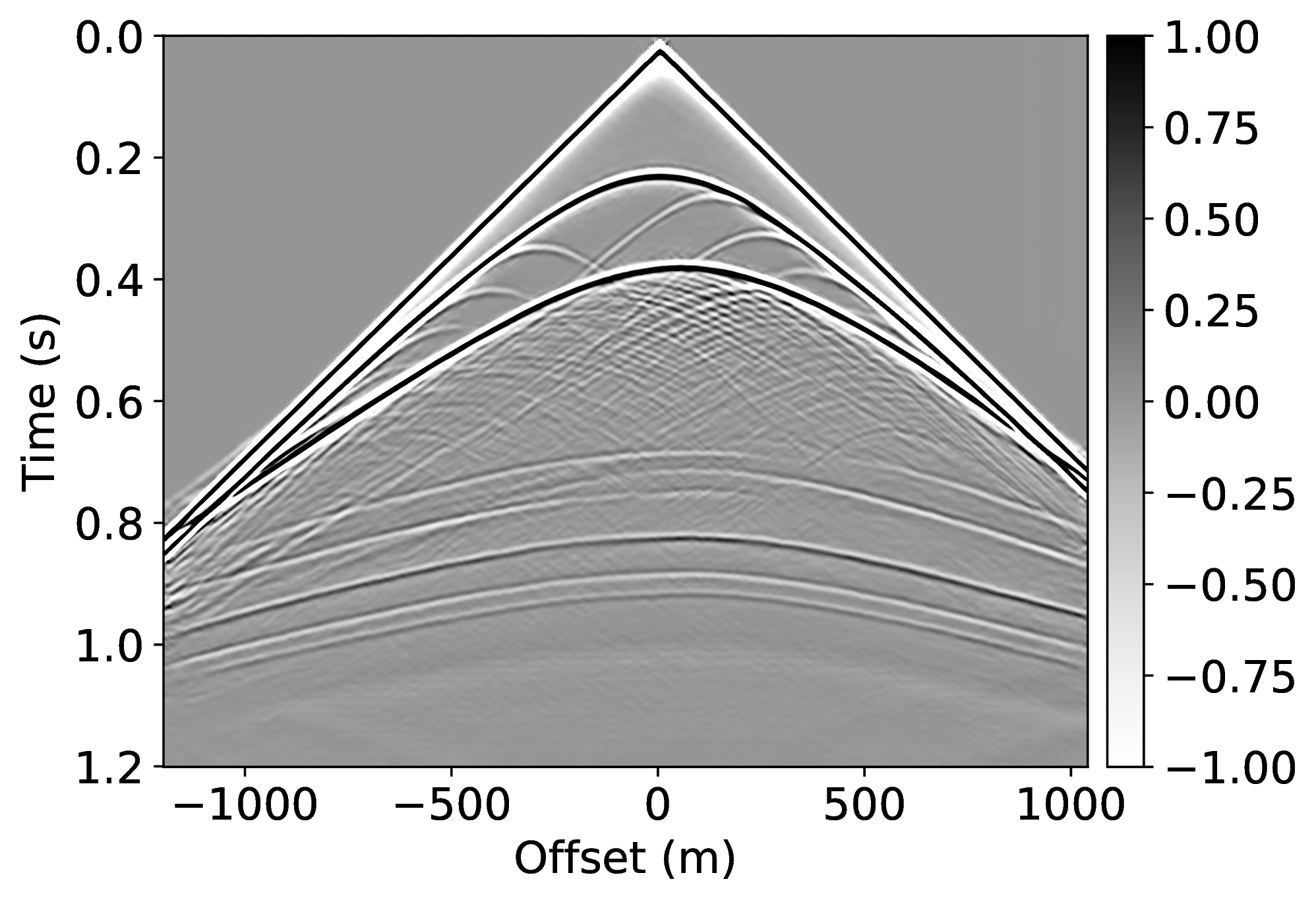
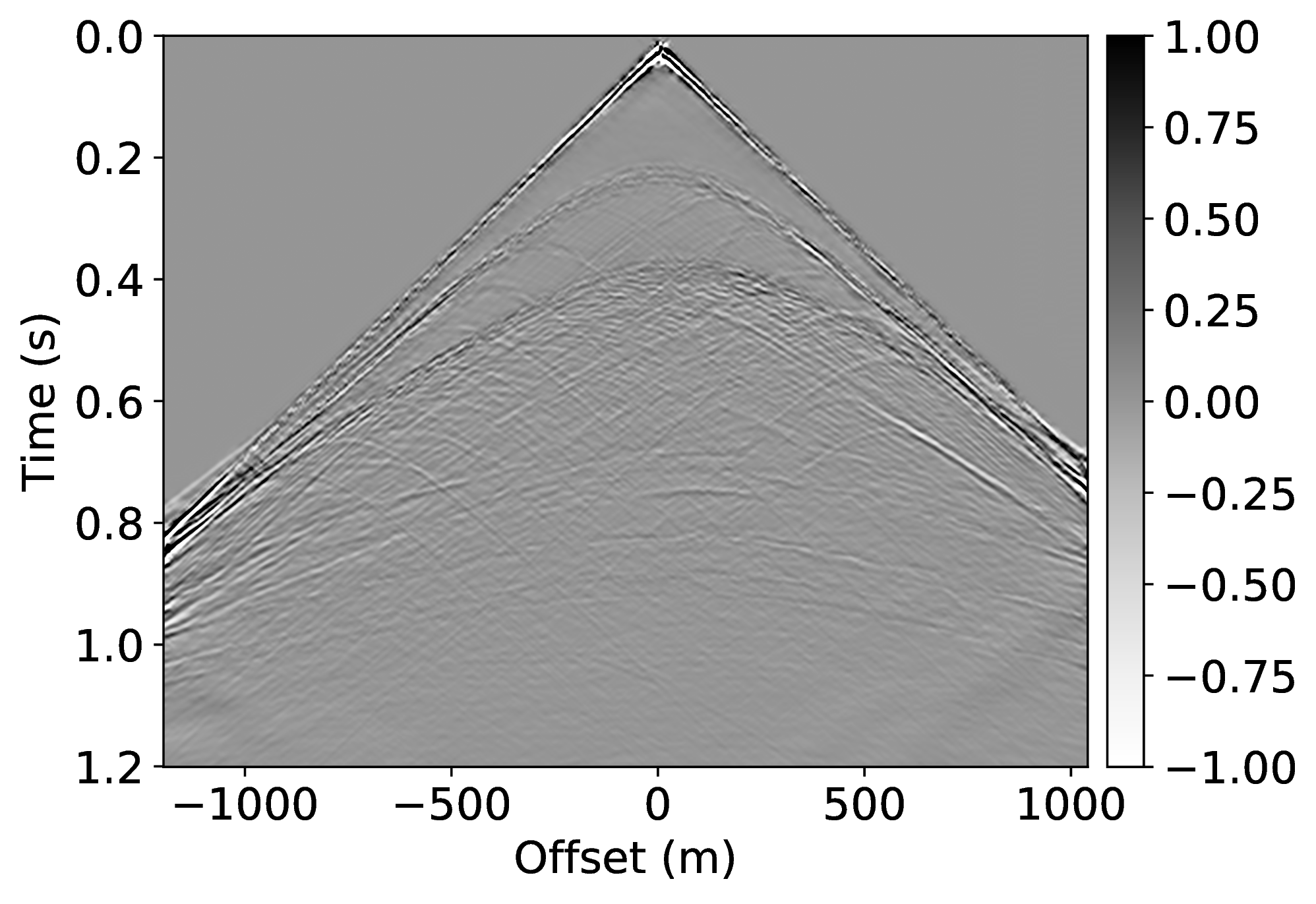
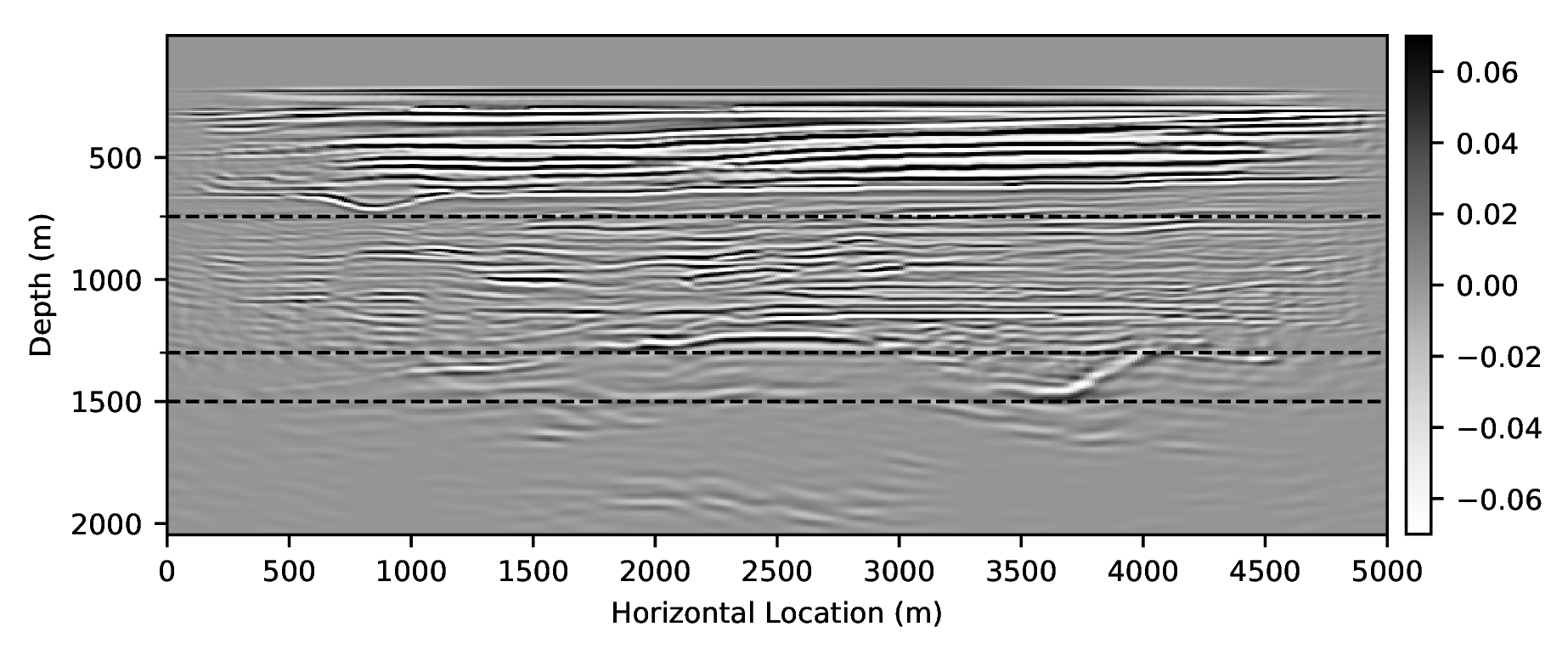
We also explore the potential of CNNs in approximating the action of the computationally expensive Estimation of Primaries by Sparse Inversion (EPSI) algorithm, applied to real data. We show that given suitable training data, consisting of a relatively cheap prediction of multiples and pairs of shot records with and without surface-related multiples, obtained via EPSI, a well-trained cnn is capable of providing an approximation to the action of the EPSI algorithm. We perform our numerical experiment on the field Nelson data set.

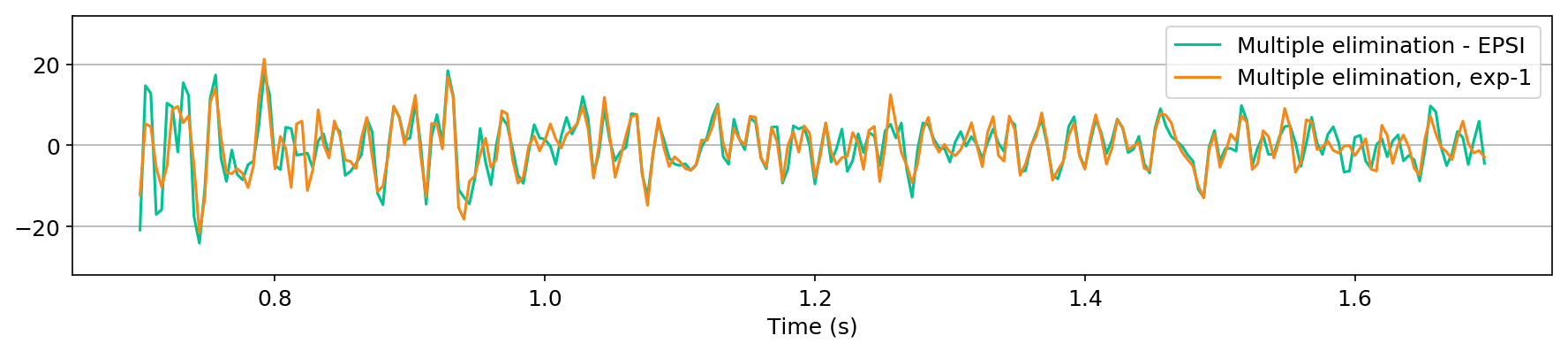
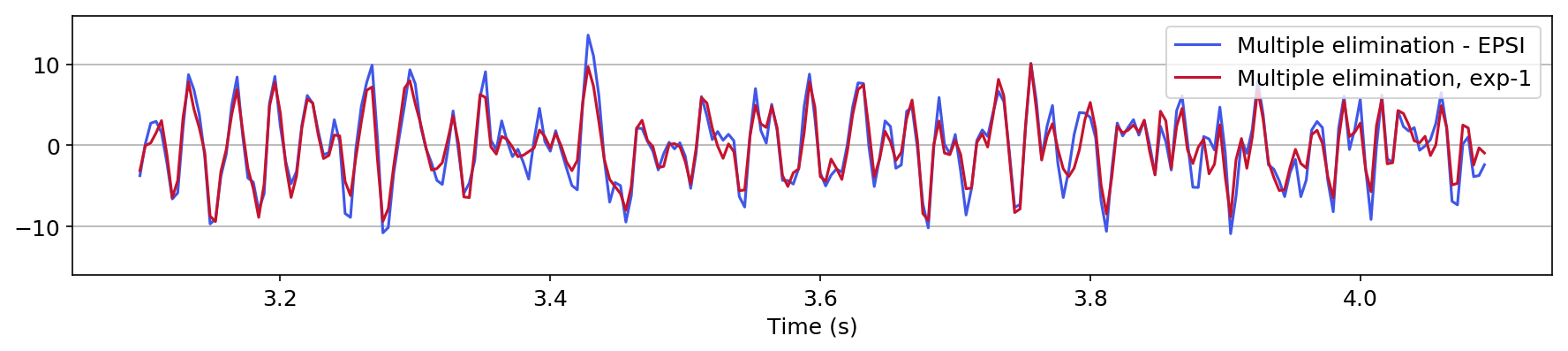
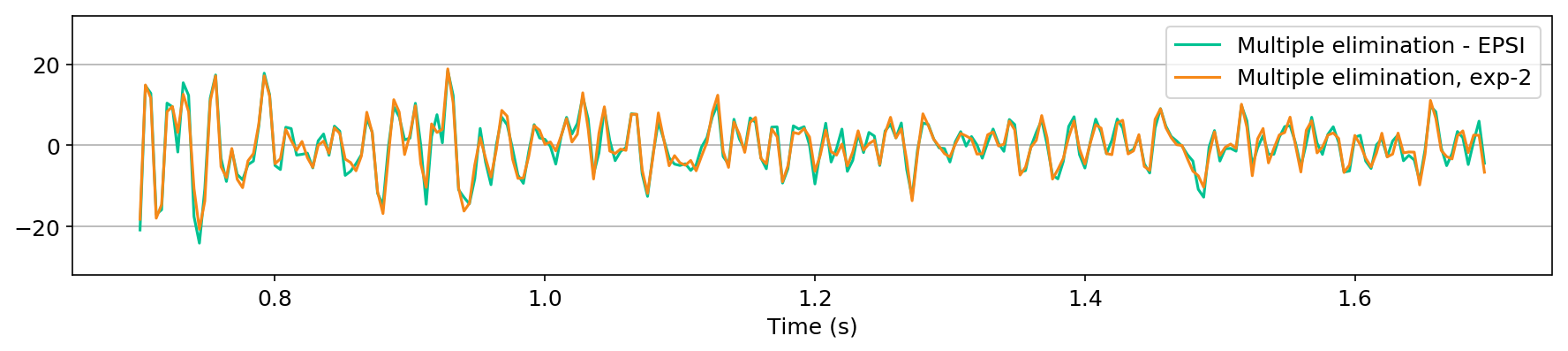
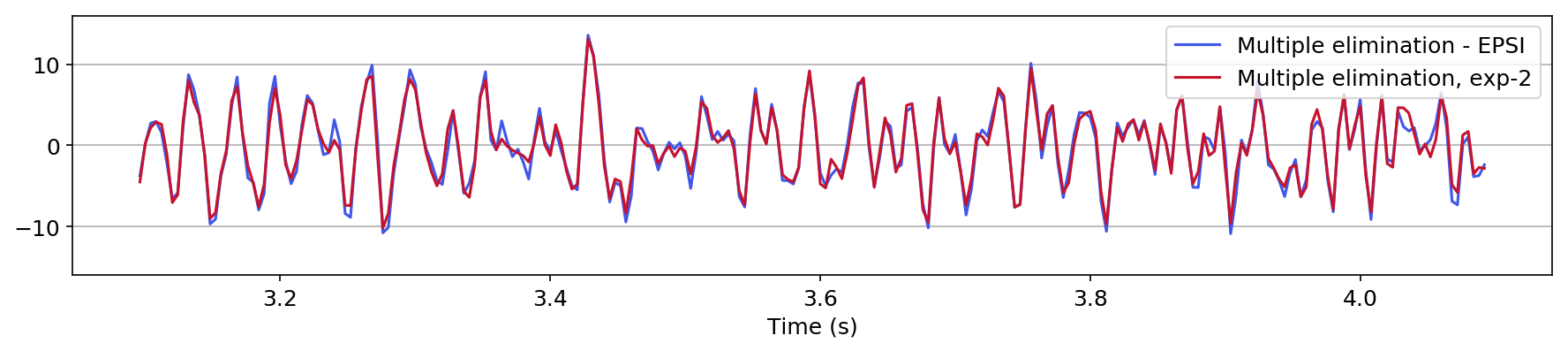
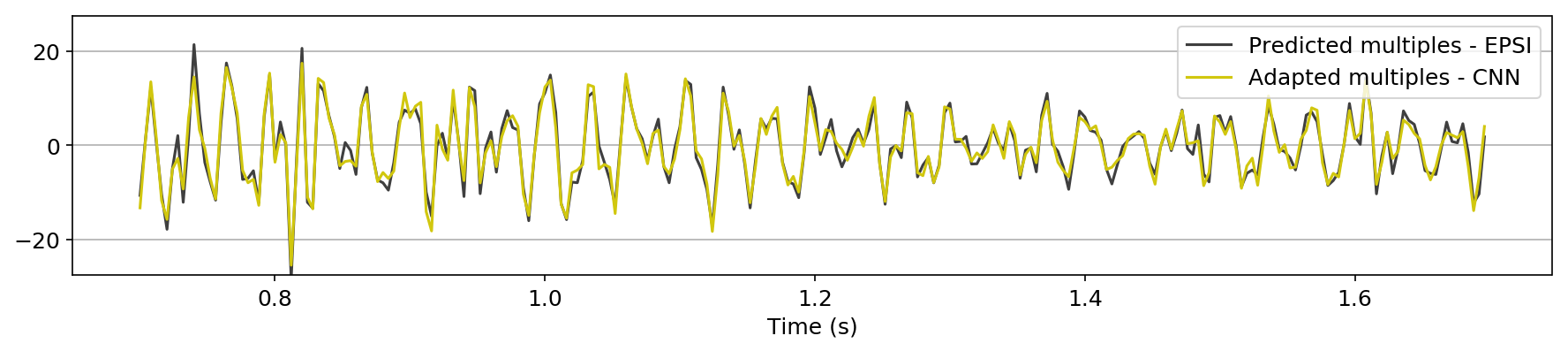
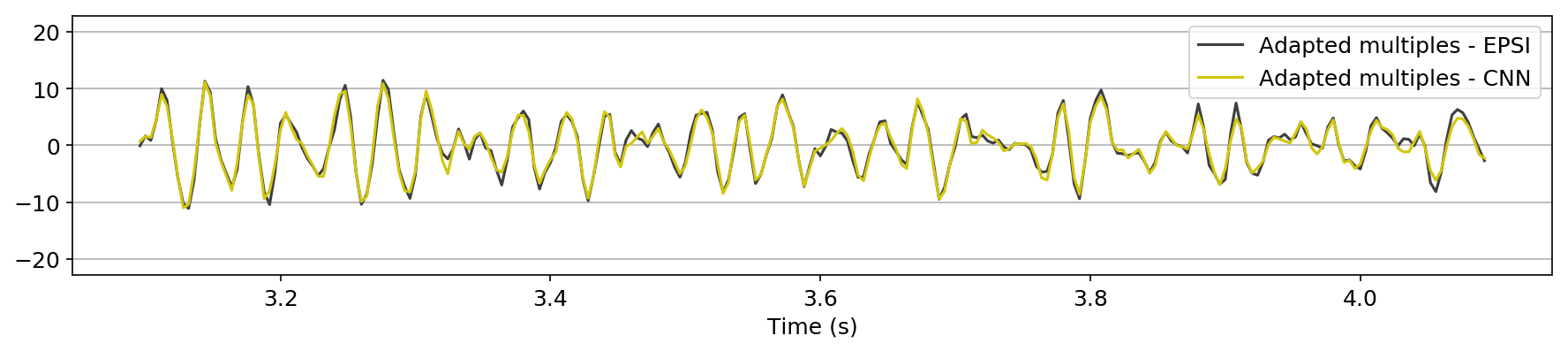
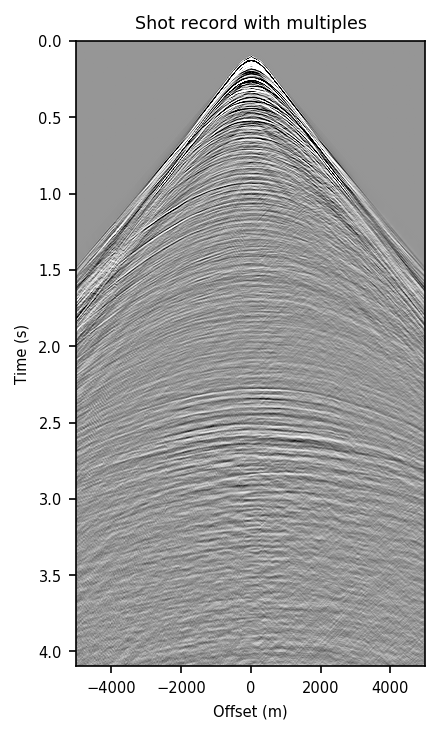
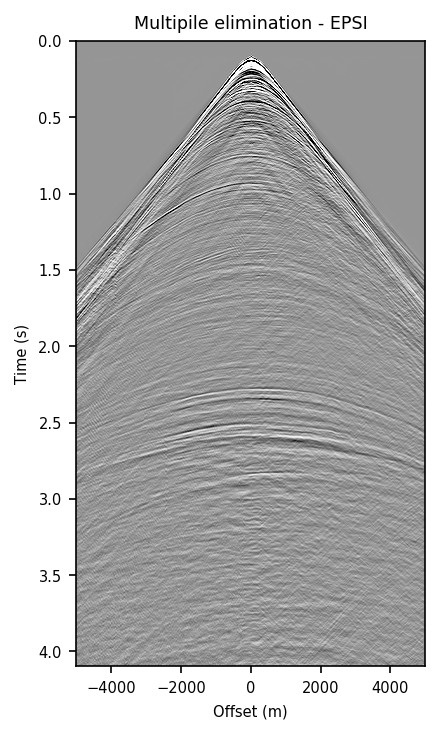
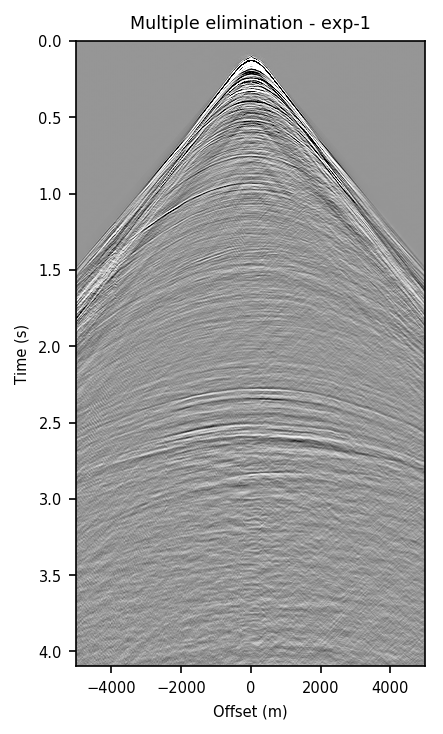
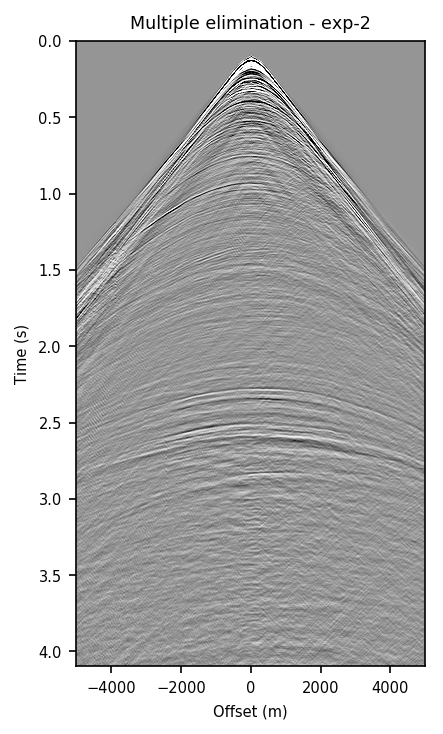
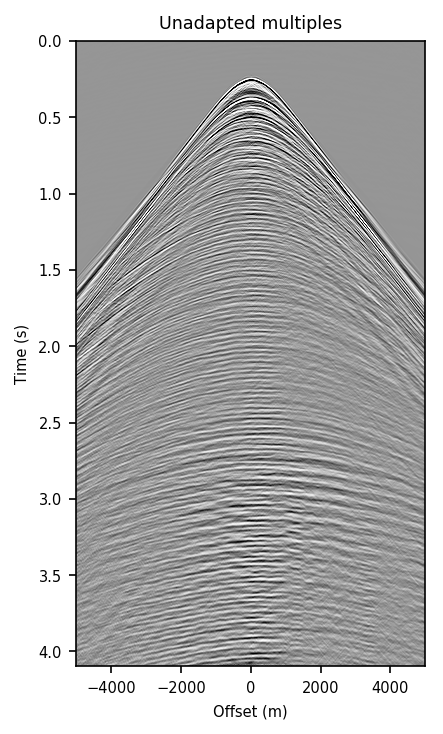
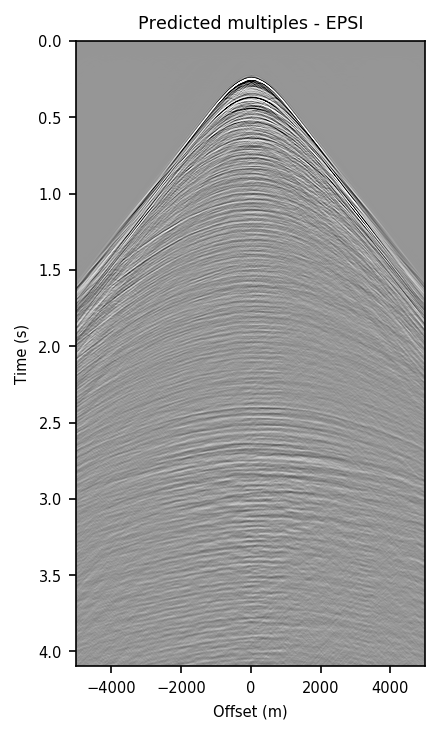
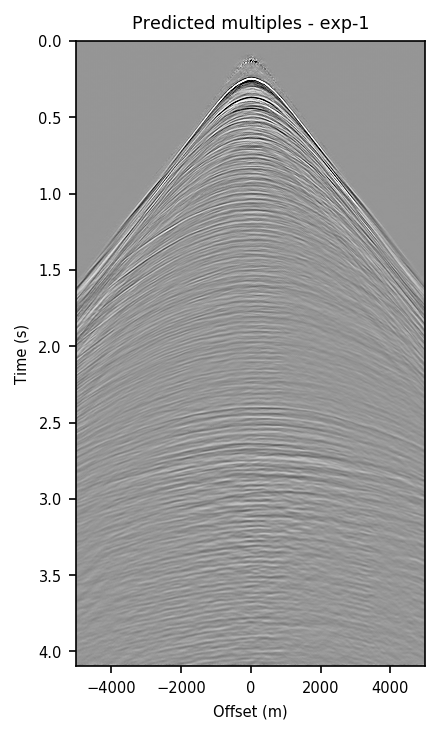
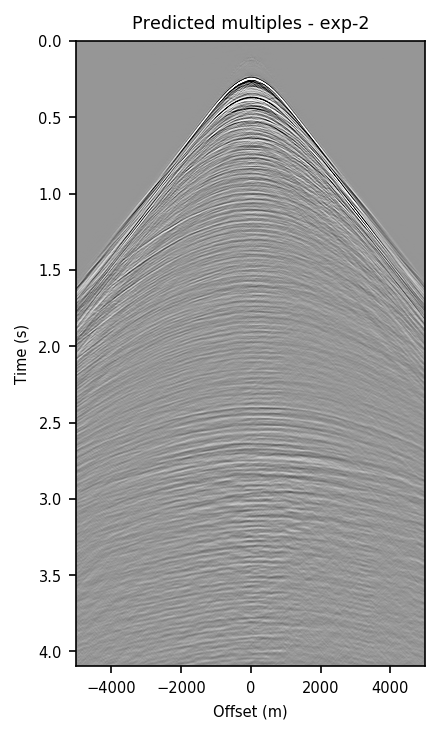
An important observation we made is that by providing the CNN with a relatively cheap prediction of multiples, obtained via a single step of surface-related multiple elimination method, without source-function correction, the accuracy of primary/multiple prediction considerably increases.

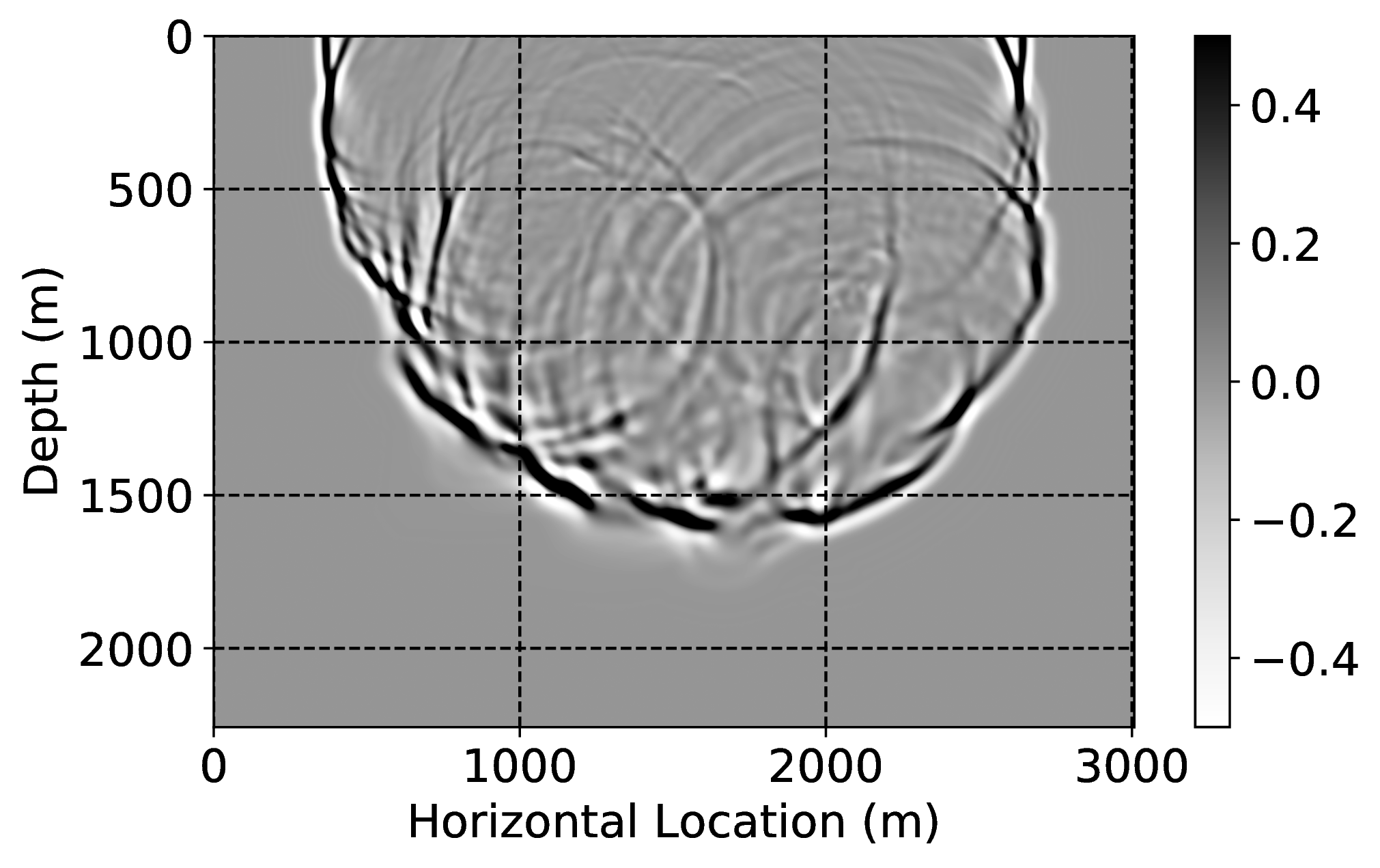
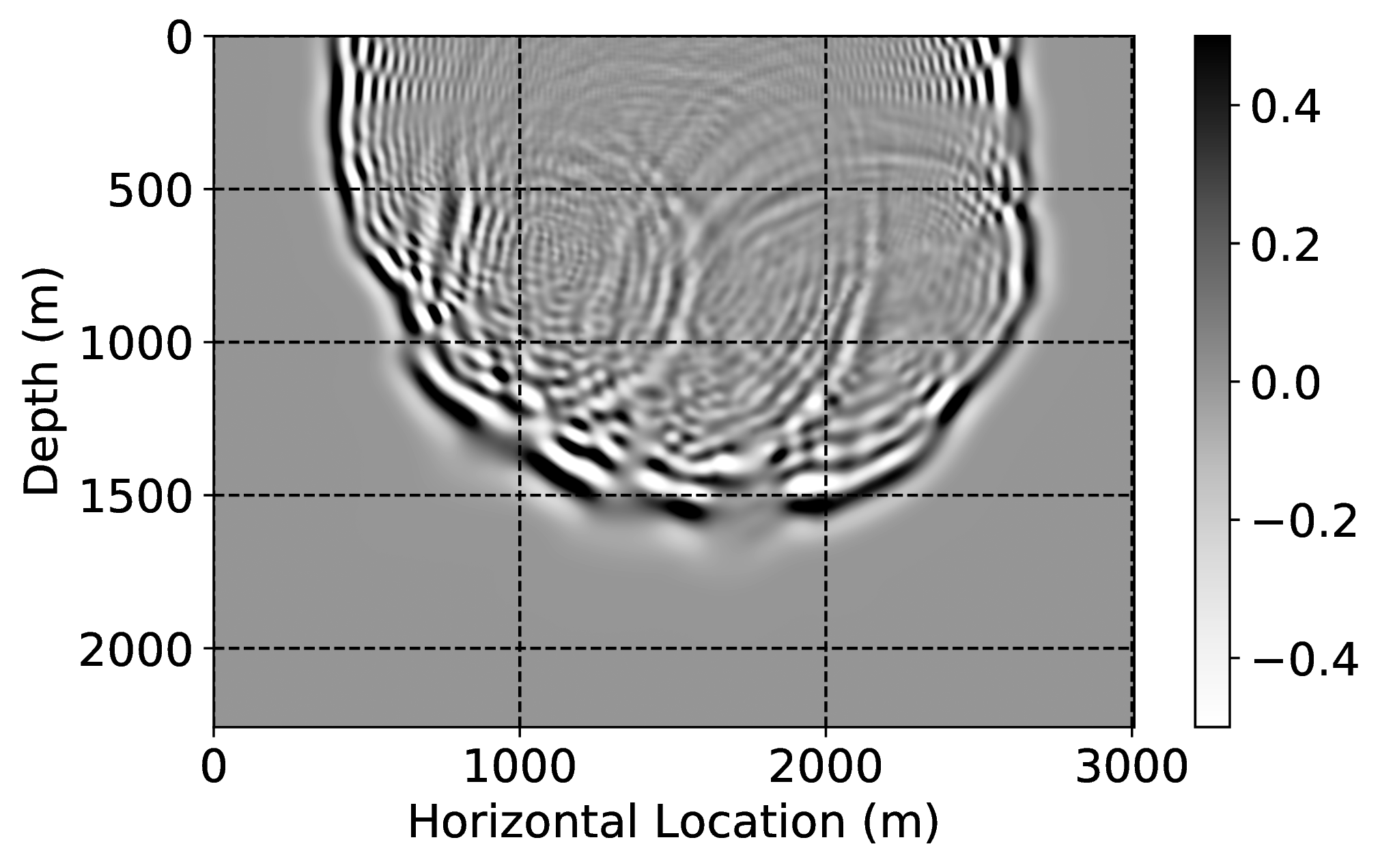
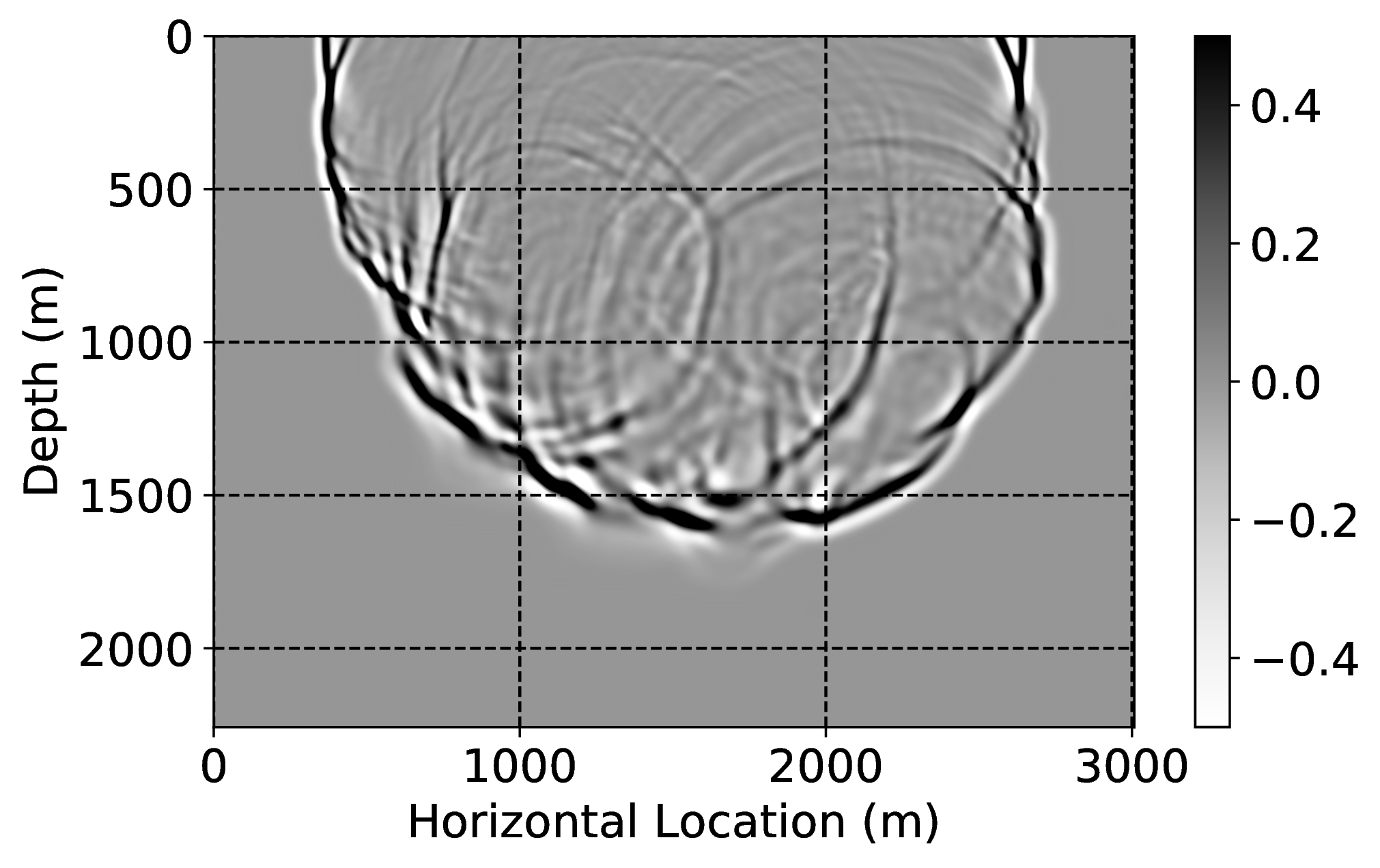
Numerical dispersion attenuation²

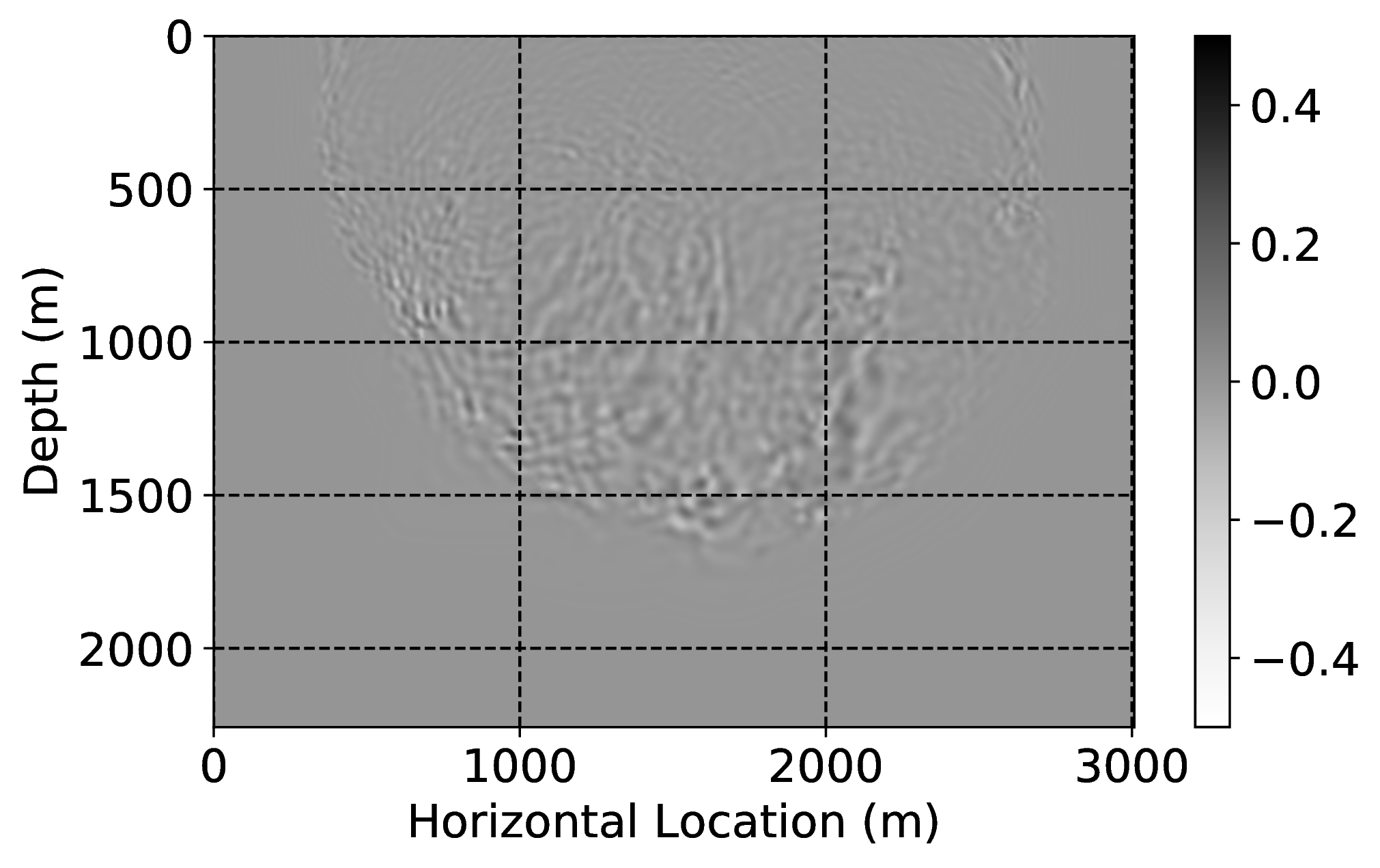
To demonstrate how CNNs handle incomplete and/or inaccurate physics, we consider two examples where we use a poor discretization (only second order) for the Laplacian. Because of this choice, our low-fidelity wave simulations are numerically dispersed, and we aim to remove the effects of this dispersion by properly trained CNNs. For this purpose, we first train a CNN on pairs of low- and high-fidelity single-shot reverse-time migrations from a background velocity model that is obtained from a “nearby” survey. We perform high-fidelity simulations by using a more expensive \(20^{\mathrm{th}}\)-order stencil. Secondly, we correct wave simulations themselves with a neural network that is trained on a family of related “nearby” velocity models. Both examples are not meant to claim possible speedups of finite-difference calculations. Instead, they are intended to demonstrate how CNNs can make non-trivial corrections such as the removal of numerical dispersion.

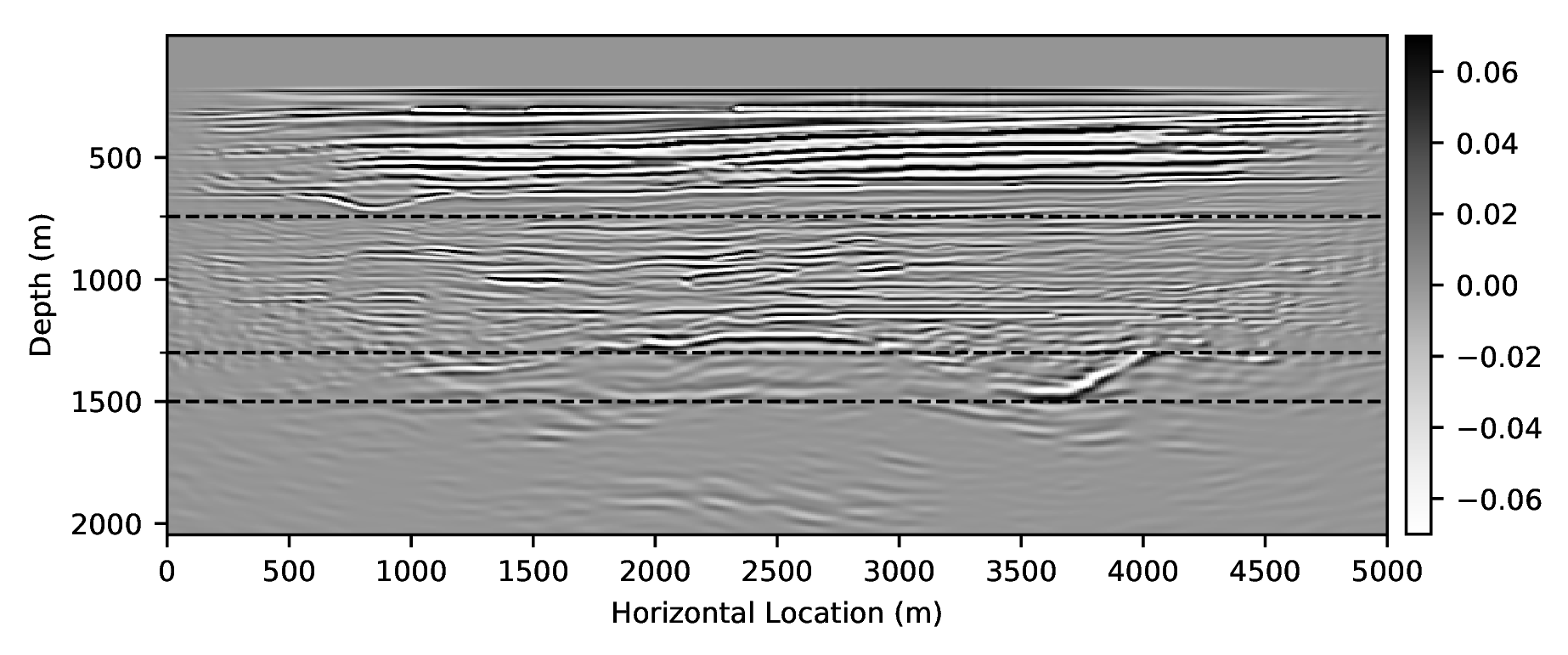
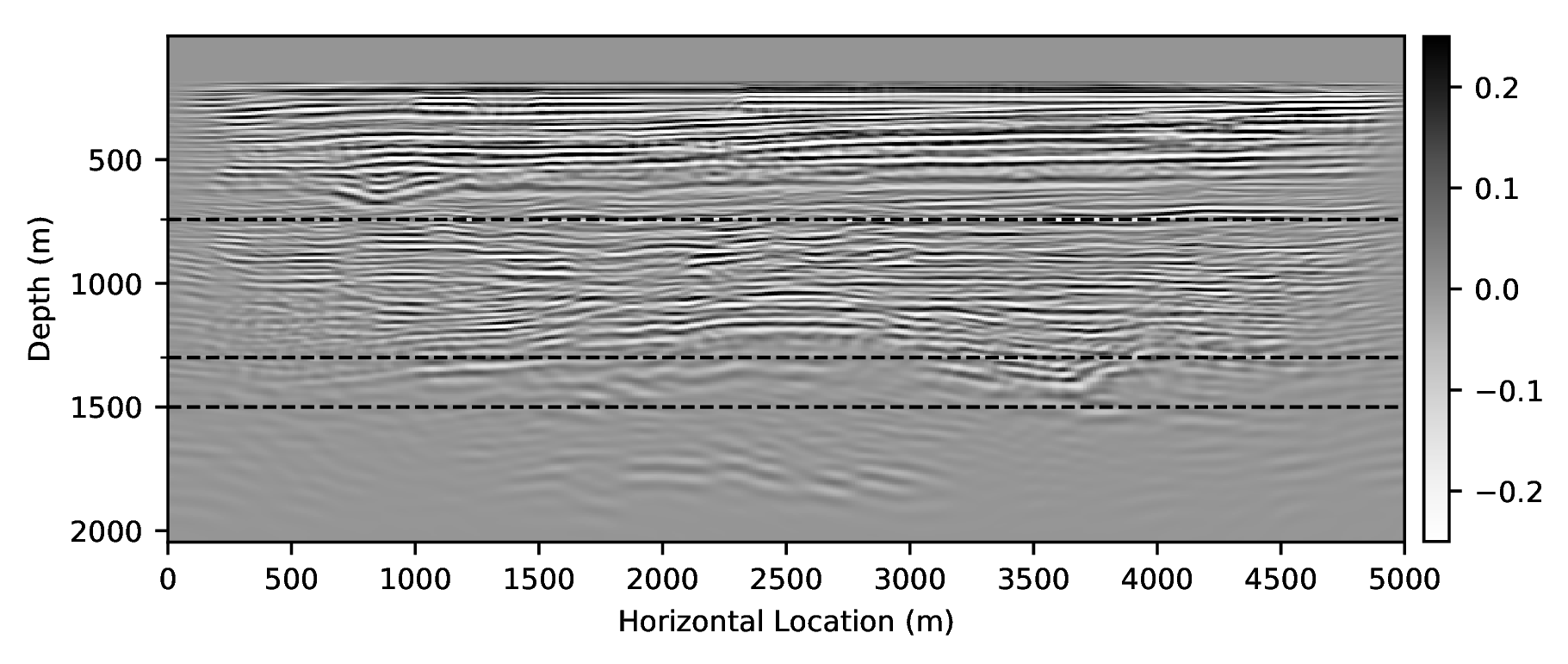
References