 |
 |
 |
 | Simply denoise: wavefield reconstruction via jittered
undersampling |  |
![[pdf]](icons/pdf.png) |
Next: Regular (under)sampling
Up: Theory
Previous: Favorable recovery conditions
Undersampling artifacts in the Fourier domain are
studied for two reasons. Firstly, several interpolation methods are
based on the Fourier transform
(Sacchi et al., 1998; Xu et al., 2005; Zwartjes and Sacchi, 2007). Secondly, the curvelet
transform, a dyadic-parabolic partition of the Fourier domain, forms
the basis of our recently-introduced recovery scheme
(Herrmann and Hennenfent, 2007). Curvelets are in many situations to be
preferred over Fourier because of their ability to sparsely represent
complex seismic data. For a detailed discussion on this topic, we
refer to Candès et al. (2005a) and Hennenfent and Herrmann (2006).
In the coming discussion, the sparsifying transform is defined as the
Fourier transform, i.e.,
 . For this definition, the vector generating the Hermitian
Toeplitz and circulant matrix
. For this definition, the vector generating the Hermitian
Toeplitz and circulant matrix
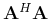 is the discrete
Fourier transform of the (under)sampling pattern. This pattern has
ones where samples are taken, zeros otherwise. Besides, the
undersampling artifacts generated by the convolution operator
is the discrete
Fourier transform of the (under)sampling pattern. This pattern has
ones where samples are taken, zeros otherwise. Besides, the
undersampling artifacts generated by the convolution operator
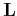 are known as spectral leakage
(Xu et al., 2005).
are known as spectral leakage
(Xu et al., 2005).
Subsections
2007-11-27
![]() . For this definition, the vector generating the Hermitian
Toeplitz and circulant matrix
. For this definition, the vector generating the Hermitian
Toeplitz and circulant matrix
![]() is the discrete
Fourier transform of the (under)sampling pattern. This pattern has
ones where samples are taken, zeros otherwise. Besides, the
undersampling artifacts generated by the convolution operator
is the discrete
Fourier transform of the (under)sampling pattern. This pattern has
ones where samples are taken, zeros otherwise. Besides, the
undersampling artifacts generated by the convolution operator
![]() are known as spectral leakage
(Xu et al., 2005).
are known as spectral leakage
(Xu et al., 2005).