Simply denoise: wavefield reconstruction via jittered undersampling

Random undersampling according to a discrete uniform distribution

When $\tensor{R}$ corresponds to a random undersampling according to a discrete uniform distribution, the situation is completely different. The matrix $\tensor{A}^H\tensor{A}$ is dense (Figure 2(c)) and the convolution matrix $\tensor{L}$ is a random matrix (Figure 2(f)). Consequently, we have

$$\tensor{A}^H\ensuremath{\mathbf{y}} = \tensor{A}^H\tensor{A}\ensu... ...mathbf{x}}_0 \approx \alpha\ensuremath{\mathbf{x}}_0 + \ensuremath{\mathbf{n}},$$ (4)

where the spectral leakage is approximated by additive white Gaussian noise $\ensuremath{\mathbf{n}}$ . For infinitely large systems (Donoho et al., 2006), this approximation becomes an equality. Because of this property, the recovery problem turns into a much simpler denoising problem, followed by a correction for the amplitudes. Remember that the acquired data $\ensuremath{\mathbf{y}}$ are noise-free (cf. equation 2) and that the noise $\ensuremath{\mathbf{n}}$ in equation 4 only comes from the underdeterminedness of the system. In other words, random undersampling according to a discrete uniform distribution spreads the energy of the spectral leakage across the Fourier domain turning the noise-free underdetermined problem (cf. equation 2) into a noisy well-determined problem (cf. equation 4) whose solution can be recovered by solving equation 3. This observation was first reported by Donoho et al. (2006).

mspl,musplREG,musplIRREG,colmspl,colmusplREG,colmusplIRREG
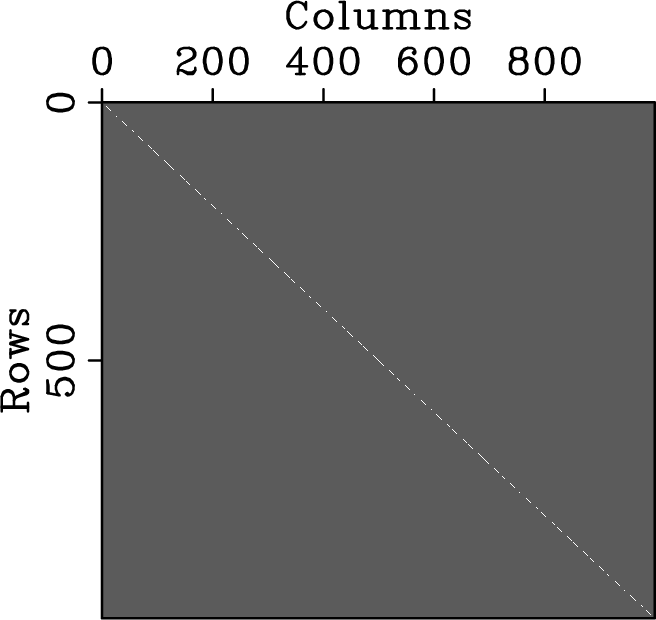
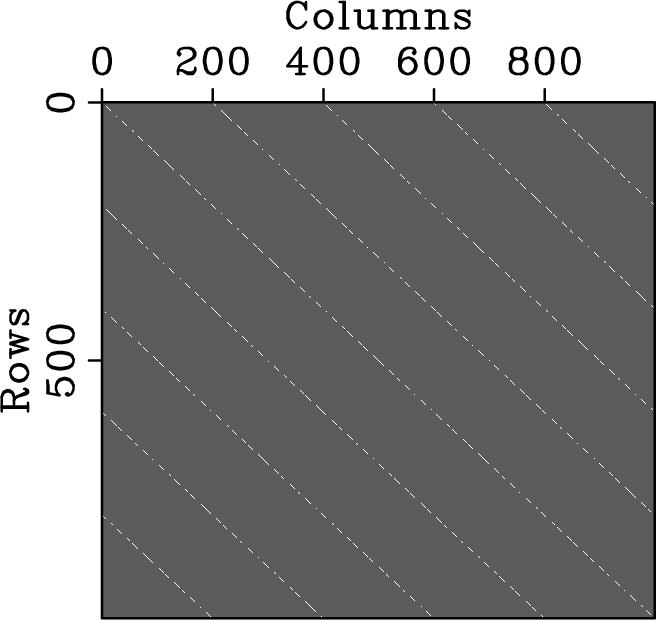
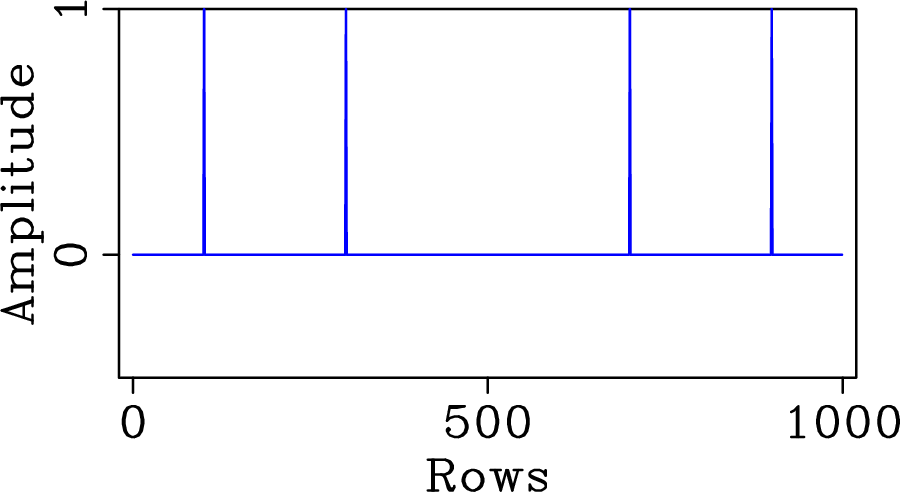
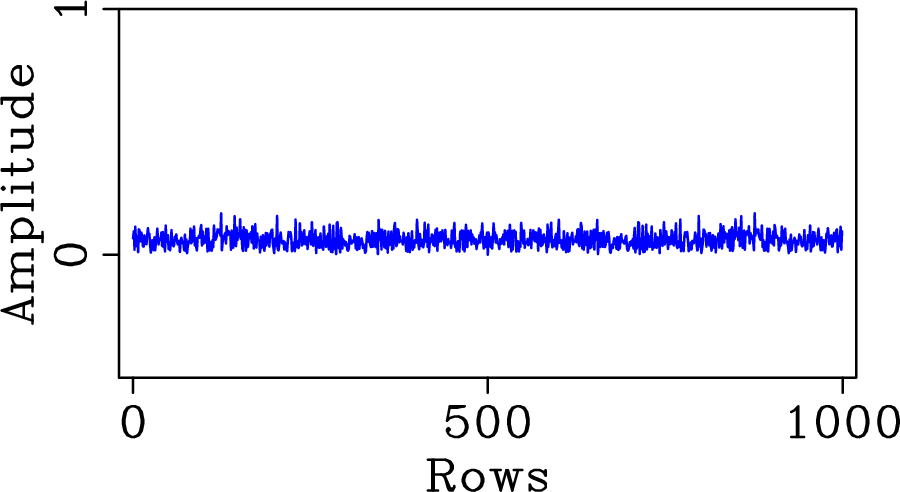
Figure 2. Convolution matrix (in amplitude) for (a) regular sampling above Nyquist rate, (b) regular five-fold undersampling, and (c) random five-fold undersampling according to a discrete uniform distribution. The respective convolution kernels (in amplitude) that generate spectral leakage are plotted in (d), (e) and (f). Despite the same undersampling factor, regular and random undersamplings produce very different spectral leakage.

Simply denoise: wavefield reconstruction via jittered undersampling