 |
 |
 |
 | Simply denoise: wavefield reconstruction via jittered
undersampling |  |
![[pdf]](icons/pdf.png) |
Next: Fourier-domain undersampling artifacts
Up: Basics of compressive sampling
Previous: Recovery by sparsity-promoting inversion
Following Verdu (1998) and Donoho et al. (2006),
we define the matrix
 to study the undersampling
artifacts
to study the undersampling
artifacts
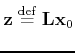 . The matrix
. The matrix
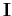 is the identity
matrix and the parameter
is the identity
matrix and the parameter 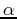 is a scaling factor such that
diag
is a scaling factor such that
diag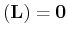 . For more general problems and
in particular in the field of digital communications, these
undersampling artifacts
. For more general problems and
in particular in the field of digital communications, these
undersampling artifacts
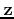 are referred to as
Multiple-Access Interference (MAI).
are referred to as
Multiple-Access Interference (MAI).
According to the CS theory (Donoho, 2006; Candès et al., 2006), the
solution
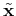 in equation 3 and
in equation 3 and
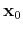 coincide when two conditions are met, namely 1)
coincide when two conditions are met, namely 1)
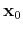 is sufficiently sparse, i.e.,
is sufficiently sparse, i.e.,
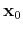 has few
nonzero entries, and 2) the undersampling artifacts are incoherent,
i.e.,
has few
nonzero entries, and 2) the undersampling artifacts are incoherent,
i.e.,
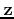 does not contain coherent energy. The first
condition of sparsity requires that the energy of
does not contain coherent energy. The first
condition of sparsity requires that the energy of
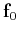 is
well concentrated in the sparsifying domain. The second condition of
incoherent random undersampling artifacts involves the study of the
sparsifying transform
is
well concentrated in the sparsifying domain. The second condition of
incoherent random undersampling artifacts involves the study of the
sparsifying transform
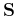 in conjunction with the restriction
operator
in conjunction with the restriction
operator
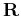 . Intuitively, it requires that the artifacts
. Intuitively, it requires that the artifacts
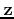 introduced by undersampling the original signal
introduced by undersampling the original signal
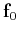 are not sparse in the
are not sparse in the
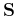 domain. When this
condition on
domain. When this
condition on
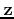 is not met, sparsity alone is no longer an
effective prior to solve the recovery problem. Albeit qualitative, the
second condition provides a fundamental insight in choosing
undersampling schemes that favor recovery by sparsity-promoting
inversion.
is not met, sparsity alone is no longer an
effective prior to solve the recovery problem. Albeit qualitative, the
second condition provides a fundamental insight in choosing
undersampling schemes that favor recovery by sparsity-promoting
inversion.
 |
 |
 |
 | Simply denoise: wavefield reconstruction via jittered
undersampling |  |
![[pdf]](icons/pdf.png) |
Next: Fourier-domain undersampling artifacts
Up: Basics of compressive sampling
Previous: Recovery by sparsity-promoting inversion
2007-11-27
 to study the undersampling
artifacts
to study the undersampling
artifacts
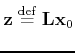 . The matrix
. The matrix
![]() in equation 3 and
in equation 3 and
![]() coincide when two conditions are met, namely 1)
coincide when two conditions are met, namely 1)
![]() is sufficiently sparse, i.e.,
is sufficiently sparse, i.e.,
![]() has few
nonzero entries, and 2) the undersampling artifacts are incoherent,
i.e.,
has few
nonzero entries, and 2) the undersampling artifacts are incoherent,
i.e.,
![]() does not contain coherent energy. The first
condition of sparsity requires that the energy of
does not contain coherent energy. The first
condition of sparsity requires that the energy of
![]() is
well concentrated in the sparsifying domain. The second condition of
incoherent random undersampling artifacts involves the study of the
sparsifying transform
is
well concentrated in the sparsifying domain. The second condition of
incoherent random undersampling artifacts involves the study of the
sparsifying transform
![]() in conjunction with the restriction
operator
in conjunction with the restriction
operator
![]() . Intuitively, it requires that the artifacts
. Intuitively, it requires that the artifacts
![]() introduced by undersampling the original signal
introduced by undersampling the original signal
![]() are not sparse in the
are not sparse in the
![]() domain. When this
condition on
domain. When this
condition on
![]() is not met, sparsity alone is no longer an
effective prior to solve the recovery problem. Albeit qualitative, the
second condition provides a fundamental insight in choosing
undersampling schemes that favor recovery by sparsity-promoting
inversion.
is not met, sparsity alone is no longer an
effective prior to solve the recovery problem. Albeit qualitative, the
second condition provides a fundamental insight in choosing
undersampling schemes that favor recovery by sparsity-promoting
inversion.