 |
 |
 |
 | Simply denoise: wavefield reconstruction via jittered
undersampling |  |
![[pdf]](icons/pdf.png) |
Next: Favorable recovery conditions
Up: Basics of compressive sampling
Previous: Basics of compressive sampling
Consider the following linear forward model for the
recovery problem
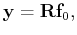 |
(1) |
where
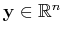 represents the acquired data,
represents the acquired data,
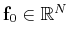 with
with 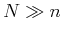 the unaliased signal to
be recovered, i.e., the model, and
the unaliased signal to
be recovered, i.e., the model, and
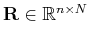 the restriction operator that collects the acquired samples from
the model. Assume that
the restriction operator that collects the acquired samples from
the model. Assume that
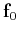 has a sparse representation
has a sparse representation
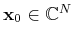 in some known transform domain
in some known transform domain
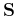 , equation 1 can now be reformulated as
, equation 1 can now be reformulated as
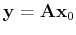 with with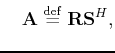 |
(2) |
where the symbol 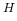 represents the conjugate transpose. As a
result, the sparsity of
represents the conjugate transpose. As a
result, the sparsity of
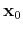 can be used to overcome the
singular nature of
can be used to overcome the
singular nature of
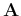 when estimating
when estimating
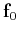 from
from
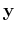 . After sparsity-promoting inversion, the recovered signal
is given by
. After sparsity-promoting inversion, the recovered signal
is given by
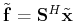 with
with
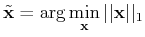 s.t. s.t.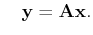 |
(3) |
In these expressions, the symbol
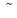 represents
estimated quantities and the
represents
estimated quantities and the 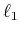 norm is defined as
norm is defined as
![$ \Vert\ensuremath{\mathbf{x}}\Vert _1\; {\buildrel\rm def\over=}\;
\sum_{i=1}^{N}\left\vert\ensuremath{\mathbf{x}}[i]\right\vert$](img29.png) , where
, where
![$ \ensuremath{\mathbf{x}}[i]$](img30.png) is
the
is
the 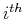 entry of the vector
entry of the vector
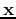 .
.
Minimizing the 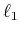 norm in equation 3 promotes
sparsity in
norm in equation 3 promotes
sparsity in
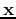 and the equality constraint ensures that the
solution honors the acquired data. Among all possible solutions of the
(severely) underdetermined system of linear equations (
and the equality constraint ensures that the
solution honors the acquired data. Among all possible solutions of the
(severely) underdetermined system of linear equations (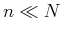 ) in
equation 2, the optimization problem in equation
3 finds a sparse or, under certain conditions, the sparsest
(Donoho and Huo, 2001) possible solution that explains the data.
) in
equation 2, the optimization problem in equation
3 finds a sparse or, under certain conditions, the sparsest
(Donoho and Huo, 2001) possible solution that explains the data.
 |
 |
 |
 | Simply denoise: wavefield reconstruction via jittered
undersampling |  |
![[pdf]](icons/pdf.png) |
Next: Favorable recovery conditions
Up: Basics of compressive sampling
Previous: Basics of compressive sampling
2007-11-27
![$ \Vert\ensuremath{\mathbf{x}}\Vert _1\; {\buildrel\rm def\over=}\;
\sum_{i=1}^{N}\left\vert\ensuremath{\mathbf{x}}[i]\right\vert$](img29.png) , where
, where
![]() norm in equation 3 promotes
sparsity in
norm in equation 3 promotes
sparsity in
![]() and the equality constraint ensures that the
solution honors the acquired data. Among all possible solutions of the
(severely) underdetermined system of linear equations (
and the equality constraint ensures that the
solution honors the acquired data. Among all possible solutions of the
(severely) underdetermined system of linear equations (![]() ) in
equation 2, the optimization problem in equation
3 finds a sparse or, under certain conditions, the sparsest
(Donoho and Huo, 2001) possible solution that explains the data.
) in
equation 2, the optimization problem in equation
3 finds a sparse or, under certain conditions, the sparsest
(Donoho and Huo, 2001) possible solution that explains the data.