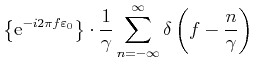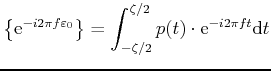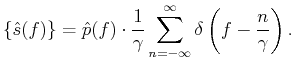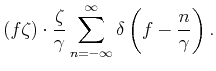|
 |
 |
 | Simply denoise: wavefield reconstruction via jittered
undersampling |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Hennenfent and Herrmann: Jittered
Previous: Conclusions
G.H. thanks Ken Bube, Ramesh Neelamani, Warren Ross,
Beatrice Vedel, and Ozgur Yilmaz for constructive discussions about
this research. D.J. Verschuur and Chevron Energy Technology Company
are gratefully thanked for the synthetic and real datasets,
respectively. The authors thank the authors of CurveLab
(www.curvelet.org) and the authors of SPGL1
(www.cs.ubc.ca/labs/scl/spgl1) for making their codes available.
This paper was prepared with Madagascar, a reproducible research
package (rsf.sourceforge.net). This work was in part financially
supported by NSERC Discovery
Grant 22R81254 and CRD Grant
DNOISE
334810-05 of F.J.H. and was carried out as part of the
SINBAD
project with support, secured through
ITF, from the following organizations:
BG Group,
BP,
Chevron,
ExxonMobil, and
Shell.
We also appreciate the valuable comments and suggestions from the two
reviewers and two associate editors.
Appendix
A
append
[app:jit]Jittered undersampling
For the convenience of the reader, we re-derive the
result originally introduced by Leneman (1966) that leads to
equation 6.
Jittered sampling locations 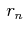 are given by
are given by
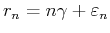 for for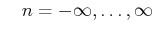 |
(10) |
The continuous random variables
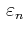 are independent and
identically distributed (iid) according to a probability density
function (pdf) p on
are independent and
identically distributed (iid) according to a probability density
function (pdf) p on
![$ [-\zeta/2,\zeta/2]$](img96.png) . The corresponding sampling
operator
. The corresponding sampling
operator 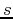 is given by
is given by
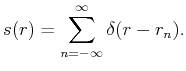 |
(11) |
Computing the Fourier transform of the previous expression yields
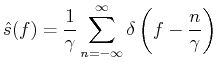 e e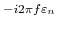 |
(12) |
which implies that
E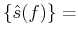 E E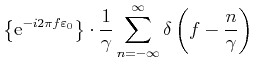 |
(13) |
since the variables
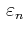 are iid. By definition, the
expected value of
are iid. By definition, the
expected value of
 e
e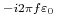 is given by
is given by
E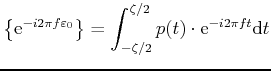 |
(14) |
which is the Fourier transform of the pdf of
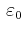 . Hence,
. Hence,
E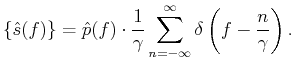 |
(15) |
Finally, for a pdf that is continuous uniform on
![$ [-\zeta/2,\zeta/2]$](img96.png) ,
the expected spectrum of the sampling operator is
,
the expected spectrum of the sampling operator is
E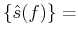 sinc sinc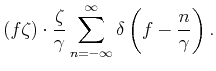 |
(16) |
This result leads us to equation 6 since the columns of
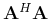 are circular-shifted versions of the Fourier
transform of the discrete jittered sampling vector, i.e.,
diag
are circular-shifted versions of the Fourier
transform of the discrete jittered sampling vector, i.e.,
diag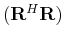 .
.
 |
 |
 |
 | Simply denoise: wavefield reconstruction via jittered
undersampling |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Hennenfent and Herrmann: Jittered
Previous: Conclusions
2007-11-27
![]() are given by
are given by
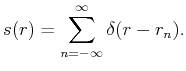
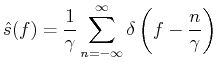 e
e