Adaptive curvelet-domain primary-multiple separation

Synthetic-data example

We consider a shot record from a synthetic line, generated by an acoustic finite-difference code for a velocity model that consists of a high-velocity layer, which represents salt, surrounded by sedimentary layers and a water bottom that is not completely flat (see Fig. 11 in Herrmann et al., 2007b). In Figure 1, the results for optimized single-term SRME are compared to curvelet-domain Bayesian separation with and without our amplitude scaling. Figures 1(a)-1(c) include the total input data with multiples, the SRME-predicted multiples and the ``multiple-free'' data, respectively. The predicted multiples are the result of conventional matching in a single window. The ``multiple-free'' data were modeled with an absorbing boundary condition, removing the surface-related multiples. Results for the estimated primaries according to optimized single-term SRME with windowed matching, Bayesian separation and scaled-Bayesian separation are included in Figures 1(d)-1(f). Comparison of these results shows a significant improvement for the primaries computed with the curvelet-domain amplitude scaling, calculated by solving Equation 4 for $\gamma =0.5$ . For this choice of $\gamma$ , the multiples are not over fitted and the amplitude correction leads to a removal of remnant multiple energy, in particular for the events annotated by the arrows. The value for $\gamma$ was found experimentally. Finally, notice that the improvement in the estimate for the primaries is due to the combination of curvelet-domain separation and scaling, yielding results that are comparable to the ones expected from multi-term SRME. Even though multi-term SRME, in combination with standard $\ell_2$ -subtraction, is known to near perfectly remove surface-related multiples for synthetic data, SRME in practice is often only viable for one iteration because field data sets often do not obey assumptions of the model. Therefore, the single-term SRME result in Figure 1(d) can be considered as state of the art.

Figure1-a,Figure1-b,Figure1-c,Figure1-d,Figure1-e,Figure1-f
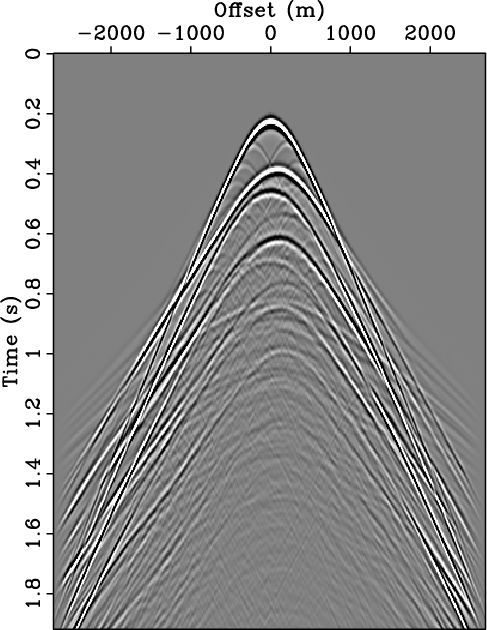
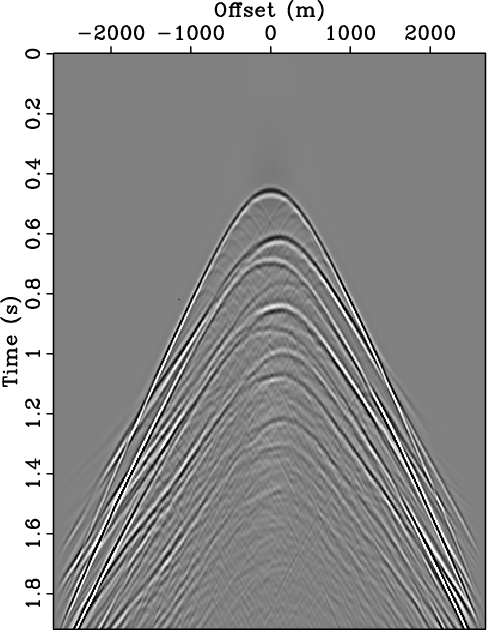
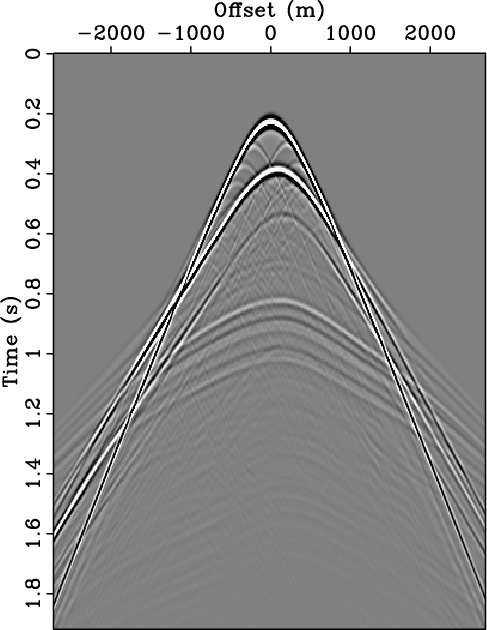
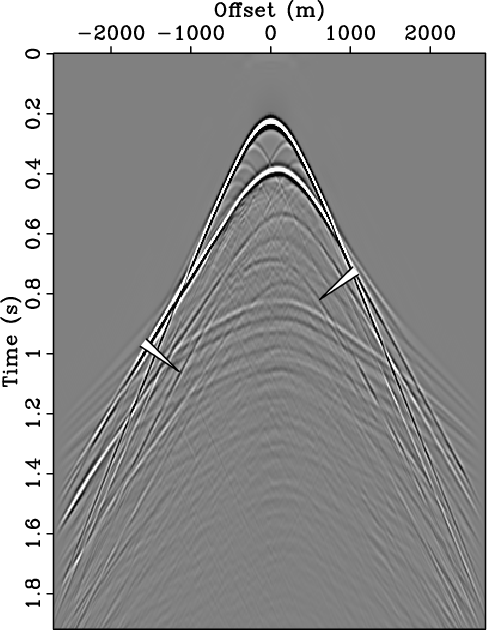
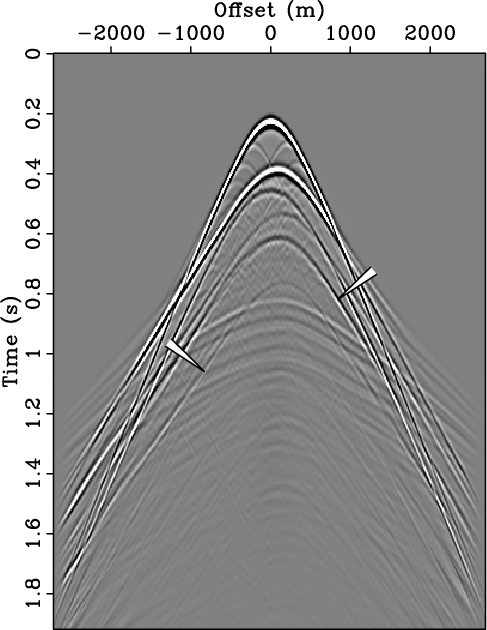
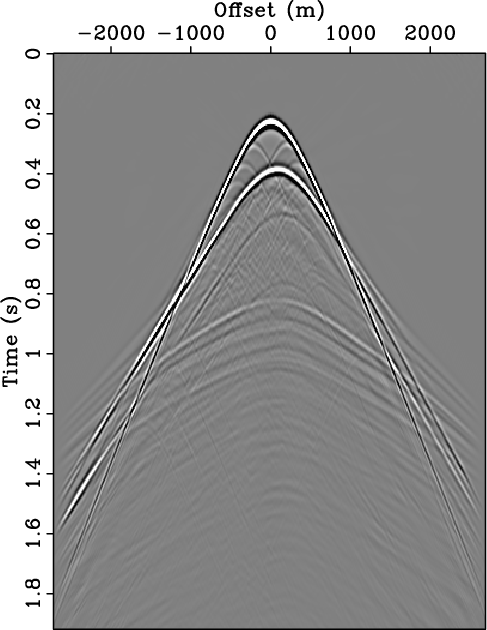
Figure 1. Primary-multiple separation on a synthetic shot record. (a) The total data, $\mathbf{p}$ , including primaries and multiples. (b) Single-term SRME-predicted multiples wavelet-matched within a global window ( ${\breve{\mathbf{s}}}_2$ ). (c) Reference surface-related multiple-free data modeled with an absorbing boundary condition. (d) Estimate for the primaries, yielded by optimized one-term SRME computed with a windowed-matched filter. (e) Estimate for the primaries, computed by Bayesian iterative thresholding with a threshold defined by $\mathbf{t}=\vert\tensor{C}{\breve{\mathbf{s}}}_2\vert$ . (f) The same as (e) but now for the scaled threshold, i.e., $\mathbf{t}=\vert\mathrm{diag}\{{\widetilde{\mathbf{w}}}\}\tensor{C}{\breve{\mathbf{s}}}_2\vert$ (with $\gamma =0.5$ ). Notice the improvement for the scaled estimate for the primaries, compared to the primaries yielded by SRME in (d) and by the Bayesian separation without scaling in (e).

Adaptive curvelet-domain primary-multiple separation