 |
 |
 |
 | Adaptive curvelet-domain primary-multiple separation |  |
![[pdf]](icons/pdf.png) |
Next: Primary-multiple separation by curvelet-domain
Up: Theory
Previous: The forward model
Curvelet-domain matched filtering
Equation 2 lends itself to an inversion for the unknown
scaling vector. As the true multiples are unknown, our formulation
minimizes the least-squares mismatch between the total data and the
predicted multiples. The following issues complicate the estimation of
the scaling vector: (i) the undeterminedness of the forward model, due
to the redundancy of the curvelet transform, i.e.,
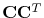 is rank deficient; (ii) the risk of
overfitting the data, which leads to unwanted removal of primary
energy, and (iii) the positivity requirement for the scaling vector. To
address issues (i-ii), the following augmented system of equations is
formed that relates the unknown scaling vector
is rank deficient; (ii) the risk of
overfitting the data, which leads to unwanted removal of primary
energy, and (iii) the positivity requirement for the scaling vector. To
address issues (i-ii), the following augmented system of equations is
formed that relates the unknown scaling vector
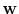 to the
augmented data vector,
to the
augmented data vector,
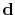 , i.e.,
, i.e.,
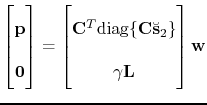 |
(3) |
or
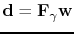 . The scaling vector is
found by minimizing the functional
. The scaling vector is
found by minimizing the functional
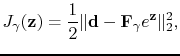 |
(4) |
where the substitution of
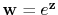 (with the
exponentiation taken elementwise) guarantees positivity (issue (iii))
of the solution (Vogel, 2002). This formulation seeks a solution
fitting the total data with a smoothness constraint imposed by the
sharpening operator
(with the
exponentiation taken elementwise) guarantees positivity (issue (iii))
of the solution (Vogel, 2002). This formulation seeks a solution
fitting the total data with a smoothness constraint imposed by the
sharpening operator
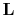 , which for each scale penalize
fluctuations amongst neighboring curvelet coefficients in the space
and angle directions (see Herrmann et al., 2007c, for a detailed
description). The amount of smoothing is controlled
by the parameter
, which for each scale penalize
fluctuations amongst neighboring curvelet coefficients in the space
and angle directions (see Herrmann et al., 2007c, for a detailed
description). The amount of smoothing is controlled
by the parameter 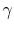 . For increasing
. For increasing 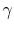 , there is more
emphasis on smoothness at the expense of overfitting the data (i.e.,
erroneously fitting the primaries). For a specific
, there is more
emphasis on smoothness at the expense of overfitting the data (i.e.,
erroneously fitting the primaries). For a specific 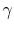 , the
penalty functional in Equation 4 is minimized with respect to
the vector
, the
penalty functional in Equation 4 is minimized with respect to
the vector
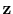 with the limited-memory BFGS
(Nocedal and Wright, 1999) with the gradient
with the limited-memory BFGS
(Nocedal and Wright, 1999) with the gradient
![$\displaystyle \mathrm{grad}J(\mathbf{z})=\mathrm{diag}\{e^{\mathbf{z}}\}\big[\tensor{F}^T_\gamma\big(\tensor{F}_\gamma e^{\mathbf{z}}-\mathbf{d}\big)\big].$](img35.png) |
(5) |
Ideally, the solution of the above optimization problem,
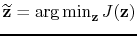 , would, after applying
the data-dependent scaling, yield the appropriate prediction for the
multiples. Unfortunately, other phase and kinematic errors may
interfere, rendering a separation based on the residual alone (as in
SRME) ineffective, i.e.,
, would, after applying
the data-dependent scaling, yield the appropriate prediction for the
multiples. Unfortunately, other phase and kinematic errors may
interfere, rendering a separation based on the residual alone (as in
SRME) ineffective, i.e.,
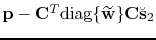 with
with
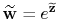 is an inaccurate estimate for the
primaries. Robustness of threshold-based primary-multiple separation
addresses this important issue and forms the second non-adaptive stage
of our separation scheme.
is an inaccurate estimate for the
primaries. Robustness of threshold-based primary-multiple separation
addresses this important issue and forms the second non-adaptive stage
of our separation scheme.
 |
 |
 |
 | Adaptive curvelet-domain primary-multiple separation |  |
![[pdf]](icons/pdf.png) |
Next: Primary-multiple separation by curvelet-domain
Up: Theory
Previous: The forward model
2008-01-18
![]() is rank deficient; (ii) the risk of
overfitting the data, which leads to unwanted removal of primary
energy, and (iii) the positivity requirement for the scaling vector. To
address issues (i-ii), the following augmented system of equations is
formed that relates the unknown scaling vector
is rank deficient; (ii) the risk of
overfitting the data, which leads to unwanted removal of primary
energy, and (iii) the positivity requirement for the scaling vector. To
address issues (i-ii), the following augmented system of equations is
formed that relates the unknown scaling vector
![]() to the
augmented data vector,
to the
augmented data vector,
![]() , i.e.,
, i.e.,