 |
 |
 |
 | Simply denoise: wavefield reconstruction via jittered
undersampling |  |
![[pdf]](icons/pdf.png) |
Next: Controlled recovery experiments for
Up: Fourier-domain artifacts of the
Previous: Optimally-jittered undersampling ( ):
In this regime, both coherent aliases and incoherent random
undersampling noise are present. Depending on the choice for the
jitter parameter, the energy either localizes or randomly spreads
across the spectrum. Again, the reduction of the aliases is related to
the locations of the zero crossings of the sinc function that move as
a function of 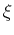 . As
. As 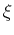 increases, the zeros move closer to the
aliases. As expected, the matrix
increases, the zeros move closer to the
aliases. As expected, the matrix
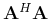 , plotted in
Figure 5(a), still contains the imprint of coherent
off-diagonals, resulting in a kernel of
, plotted in
Figure 5(a), still contains the imprint of coherent
off-diagonals, resulting in a kernel of
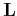 , included in
Figure 5(c), that is a superposition of coherent
aliases and incoherent random noise. Although this regime reduces the
aliases, coherent energy remains in the undersampling artifacts. This
residue creates a situation that is less favorable for recovery.
Depending on the relative strength of the aliases compared to the
magnitude
, included in
Figure 5(c), that is a superposition of coherent
aliases and incoherent random noise. Although this regime reduces the
aliases, coherent energy remains in the undersampling artifacts. This
residue creates a situation that is less favorable for recovery.
Depending on the relative strength of the aliases compared to the
magnitude 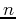 of the diagonal of
of the diagonal of
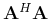 , recovery
becomes increasingly more difficult, an observation that can be
established experimentally.
, recovery
becomes increasingly more difficult, an observation that can be
established experimentally.
In the next section, a series of controlled experiments is conducted
to compare the recovery from regularly, randomly according to a
discrete uniform distribution and optimally-jittered undersamplings.



|
|---|
musplJIT,musplJITo,colmusplJIT,colmusplJITo
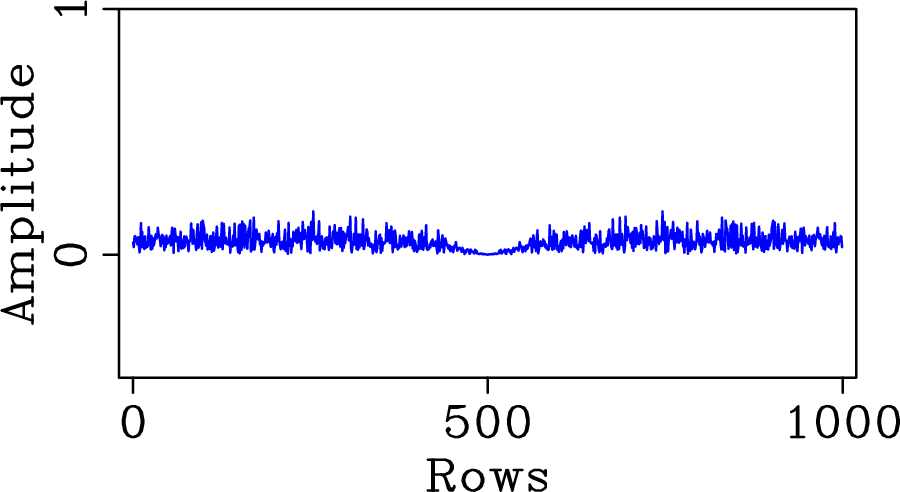
Figure 5. Jittered
undersampling according to a discrete uniform distribution. (a)
Suboptimal and (b) optimal jittered five-fold undersampling
convolution matrices (in amplitude). The respective convolution
kernels (in amplitude) that generate spectral leakage are plotted in
(c) and (d). If the regular undersampling points are not shuffled
enough, only part of the undersampling artifacts energy is spread,
the rest of the energy remaining in weighted aliases. When there is
just enough shuffling, all the undersampling artifacts energy is
spread making jittered undersampling like random undersampling, yet
controlling the size of the largest gap between two data points.
|
|---|
![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[png]](icons/viewmag.png) ![[scons]](icons/configure.png)
|
|---|
 |
 |
 |
 | Simply denoise: wavefield reconstruction via jittered
undersampling |  |
![[pdf]](icons/pdf.png) |
Next: Controlled recovery experiments for
Up: Fourier-domain artifacts of the
Previous: Optimally-jittered undersampling ( ):
2007-11-27



