Simply denoise: wavefield reconstruction via jittered undersampling

Definition of the jittered grid

The basic idea of jittered undersampling is to regularly decimate the interpolation grid and subsequently perturb the coarse-grid sample points on the fine grid. As for random undersampling according to a discrete uniform distribution, where each location is equally likely to be sampled, a discrete uniform distribution for the perturbation around the coarse-grid points is considered (see Appendix A and Leneman (1966) for more details).

To keep the derivation of our jittered undersampling scheme succinct, the undersampling factor, $\gamma$ , is taken to be odd, i.e., $\gamma=1,\,3,\,5,\,\ldots$ We also assume that the size $N$ of the interpolation grid is a multiple of $\gamma$ so that the number of acquired data points $n=N/\gamma$ is an integer. For these choices, the jittered-sampled data points are given by

$$\ensuremath{\mathbf{y}}[i] = \ensuremath{\mathbf{f}}_0[j] \quad i=1,\ldots,n \quad j = \underbrace{\frac{1-\gamma}{2} +\gamma\cdot i}_{\text{deterministic}} + \underbrace{\epsilon_i}_{\text{random}},$$ (5)

where the discrete random variables $\epsilon_i$ are integers independently and identically distributed (iid) according to a uniform distribution on the interval between $-\lfloor(\xi-1)/2\rfloor$ and $\lfloor(\xi-1)/2\rfloor$ . The jitter parameter $0\leq\xi\leq\gamma$ relates to the size of the perturbation around the coarse regular grid. The floor function of a real number $q$ , denoted $\lfloor q\rfloor$ , is a function that returns the highest integer less than or equal to $q$ . The above sampling can be adapted for the case $\gamma$ is even.

schemjit
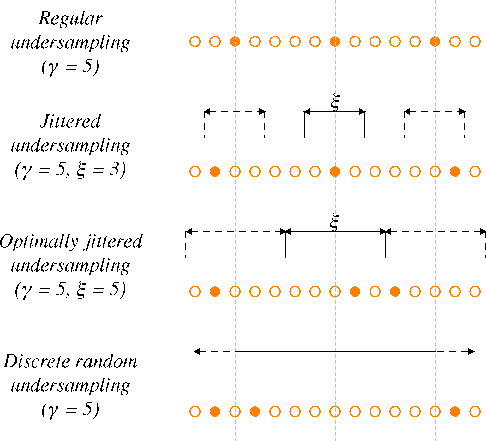
Figure 3. Schematic comparison between different undersampling schemes. The circles define the fine grid on which the original signal is alias-free. The solid circles represent the actual sampling points for the different undersampling schemes. The jitter parameter $\xi$ relates to how far the actual jittered sampling point can be from the regular coarse grid, effectively controlling the size of the maximum acquisition gap.

In Figure 3, schematic illustrations are included for samplings with increasing randomness. The fine grid of open circles denotes the interpolation grid on which the model $\ensuremath{\mathbf{f}}_0$ is defined. The solid circles correspond to the coarse sampling locations. These illustrations show that for jittered undersampling, the maximum gap size can not exceed $(\gamma-1)+2\cdot\lfloor(\xi-1)/2\rfloor$ data points. For regular undersampling, all the gaps are of size $\gamma-1$ and for random undersampling according to a discrete uniform distribution, the maximum gap size is $N-n$ . Remember that the number of samples is the same for each of these undersampling schemes.

As mentioned earlier, recovery with localized transforms depends on both the maximum gap size and a sufficient sampling randomness to break the coherent aliases. In the next section, we show how the value of the jitter parameter controls these two aspects in our undersampling scheme.

Simply denoise: wavefield reconstruction via jittered undersampling