Example Set 1

This examples is for the SLIMpy beginer. We will build up to solving the l1 minimization problem. We denote y a seismic trace corrupted by swell noise. A possible approach to denoising takes advantage of the sparsity of swell noise in the DCT domain and of seismic signal in the wavelet domain. The forward problem is as follows:

$\textbf{y} = \left[ \begin{array}{ccc} \textbf{PC} & \vline & \textbf{W} \end{array}\right] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_N \\ \hline x_{N+1} \\ \vdots \\ x_{2N} \end{array}\right]$

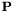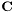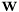In this equation, $\left[ \begin{array}{ccc} x_1 & \ldots & x_N \end{array}\right]^T$ represents the DCT contribution in the total data and $\left[ \begin{array}{ccc} x_{N+1} & \ldots & x_{2N} \end{array}\right]^T$ the wavelet contribution. The operators $\textbf{P}$ , $\textbf{C}$ , and $\textbf{W}$ are a frequency weighting, the DCT, and the wavelet transforms, respectively. The inverse problem is as follows:

$\tilde{\textbf{x}} = \arg\min \|\textbf{x}\|_1\quad\mbox{s.t.}\quad\left[ \begin{array}{ccc} \textbf{PC} & \vline & \textbf{W} \end{array}\right]\textbf{x}=\textbf{y}$

and the denoise signal, s , is given by

$\textbf{s} = \textbf{W} \left[ \begin{array}{c} \tilde{x}_{N+1} \\ \vdots \\ \tilde{x}_{2N} \end{array}\right].$

Learing objectives:

To start a simple slimpy script.
Learn about SLIMpy.
Create a black box package to solve a general problem

Inputs:

swellnoise.rsf the synthetic model of the swell noise
sig.rsf the synthetic model of the data
data.rsf the synthetic model produced from sfsigmoid

Outputs:

esig.rsf the esimated signal
enoise.rsf the esimated noise
residual.rsf the diffrence between the data, esimated signal and esimated noise

Prerequisite:

SLIMpy and ContribSLIMpy
Madagascar
SCons
All steps require `scons' to be run from the Set1 directory to create inputs.

Step 1

Link: Step 1 This is the very first example you should look at when learning SLIMpy

Objectives:

get SLIMpy ready to use
become familiar with the python syntax
do a simple non-iterative de-noise with surfacelets

Step 2

Link: Step 2

Objectives:

Integrate the previous example with SCons and Madagascar reproducibility
Perform a dot-test on a linear operator

Step 3

Link: Step 3 In this step we will build a slimpy script to solve the problem:

$\tilde{\textbf{x}} = \arg\min \|\textbf{x}\|_1\quad\mbox{s.t.}\quad \textbf{C} \textbf{x}+\epsilon=\textbf{y}$

where C is the cosine transform and x is the swell noise and 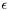$\epsilon$ is the signal. I will use the existing thresholded landweber solver with a linear threshold cooling scheme.

Objectives:

Use an exsiting iterative solver

Step 4

Link: Step 4 The next step is to create a compound operator PC where P is the diagonal weighting on the range of C.

$\tilde{\textbf{x}} = \arg\min \|\textbf{x}\|_1\quad\mbox{s.t.}\quad \textbf{PC} \textbf{x}+\epsilon=\textbf{y}$

Objectives:

Create a compound operator
Learn more of the builtin SLIMpy Options

Step 5

Link: Step 5 Solve the full problem

$\tilde{\textbf{x}} = \arg\min \|\textbf{x}\|_1\quad\mbox{s.t.}\quad\left[ \begin{array}{ccc} \textbf{PC} & \vline & \textbf{W} \end{array}\right]\textbf{x}=\textbf{y}$

Objectives:

Create an Augmented system of equations
Change verbosity of the output

Additional inputs:

'lowfweight.rsf'

Additional outputs:

'residual.rsf'

Step 6

Link: Step 6

Objectives:

Make the script more portable and easy to use by using the built-in solve builder

Step 7

Link: Step 7

Objectives:

Make the script more portable and easy to use by using the slimproj Solve builder
Create a SLIMpy application by encapsulating the problem in a portable python module.

Additional inputs:

'lowfweight.rsf'
'swellsep.py' contains definition of swell separation problem

Additional outputs:

'residual.rsf'