Abstract
Recently, we demonstrated that combining joint recovery with low-cost non-replicated randomized sampling tailored to time-lapse seismic can give us access to high fidelity, highly repeatable, dense prestack vintages, and high-grade time-lapse. To arrive at this result, we assumed well-calibrated surveys—i.e., we presumed accurate post-plot source/receiver positions. Unfortunately, in practice seismic surveys are prone to calibration errors, which are unknown deviations between actual and post-plot acquisition geometry. By means of synthetic experiments, we analyze the possible impact of these errors on vintages and on time-lapse data obtained with our joint recovery model from compressively sampled surveys. Supported by these experiments, we demonstrate that highly repeatable time-lapse vintages are attainable despite the presence of unknown calibration errors in the positions of the shots. We assess the repeatability quantitatively for two scenarios by studying the impact of calibration errors on conventional dense but irregularly sampled surveys and on low-cost compressed surveys. To separate time-lapse effects from calibration issues, we consider the idealized case where the subsurface remains unchanged and the practical situation where time-lapse changes are restricted to a subset of the data. In both cases, the quality of the recovered vintages and time-lapse decreases gracefully for low-cost compressed surveys with increasing calibration errors. Conversely, the quality of vintages from expensive densely periodically sampled surveys decreases more rapidly as unknown and difficult to control calibration errors increase.
Introduction
The current paradigm in time-lapse (4D) seismic necessitates expensive replication of the baseline during the monitor survey to attain high degrees of repeatability (Eiken et al., 2003; Brown and Paulsen, 2011). In contrast, motivated by the successful field application of randomized Compressive Sensing surveys (Mosher et al., 2014) pioneered by F. J. Herrmann (2010) and related works, our recent findings (Oghenekohwo et al., 2017; Wason et al., 2017) suggest that one does not need to replicate subsampled randomized time-lapse surveys to get equivalent and acceptable levels of repeatability. While these results are encouraging, our findings relied on two critical assumptions, namely we ignored noise and assumed calibrated surveys. Although our randomized time-lapse acquisition does not insist on exact replication in the field — allowing for deviations between planned (pre-plot) and actual survey geometries — reconstruction of the vintages towards a common fine periodic grid from the randomized samplings relies on accurate knowledge of the actual acquisition parameters. Thus, we ignore possible unknown calibration errors defined as differences between the actual (true) and observed (recorded) post-plot geometries.
Since these calibration errors are unavoidable in practice, we study the performance of our approach, namely, compressed time-lapse acquisition with calibration errors and subsequent recovery with our joint recovery model (JRM), via a series of experiments designed to measure attainable degrees of repeatability. As before, key to our success is the sparse recovery of the component common to the vintages, and “innovations” with respect to this component that sparsely encode the differences between the vintages. Because the common component is sensed by all time-lapse surveys, recovery with the JRM leads to improved quality of the vintages when the surveys are not replicated as we confirmed with a specific compressive sensing-inspired acquisition design (time-jittered sources in marine by Wason and Herrmann (2013)).
There have been earlier attempts (Eggenberger et al., 2014), with sparsity promotion to recover more repeatable time-lapse surveys but these also relied on having well-calibrated surveys albeit these approaches do not exploit the possible advantages distributed compressive sensing (DCS, Baron et al., 2009) has to offer but instead rely on having access to multiple periodically but coarsely sampled wavefield components for their reconstruction. By combining random subsampling and joint recovery, we are able to obtain high-quality repeatable vintages from significantly fewer calibrated measurements (Oghenekohwo et al., 2017; Wason et al., 2017).
Practitioners of time-lapse seismic studies often use the normalized root mean square (NRMS, Kragh and Christie, 2002) to quantify the degree of repeatability in 4D seismic. Repeatability, which measures similarity between vintages, depends on several factors including unknown positioning errors for each survey (Schisselé et al., 2009), differences in noise, and processing workflows (Rickett and Lumley, 2001; Hicks et al., 2014) that aim to preserve the 4D signal. The smaller the NRMS value, the less likely it is that the 4D signal is due to differences amongst the surveys or environment (currents, wave heights, etc.) the surveys were acquired in.
Our main contribution is to demonstrate that high quality and highly repeatable surveys are attainable with our JRM despite the presence of unknown calibration errors. We substantiate this claim by measuring the recovery quality and repeatability in terms of signal-to-noise ratios (S/N) and NRMS values for a series of carefully designed idealized — ignoring noise and environmental changes — randomized time-lapse surveys for which (i) there are no time-lapse changes present so worsening recovery quality and repeatability can solely be attributed to calibration errors and (ii) time-lapse changes are confined to subsets of the data.
We first describe a primer on how compressive sensing can be setup in marine acquisition before presenting the main aspects of the paper. The main paper is organized as follows. First, we present the theoretical framework for low-cost randomized time-lapse subsampled data acquisition and recovery with the JRM. Next, we introduce the NRMS in the two settings where either the earth model remains unchanged or where there is a time-lapse signal present in a subset of the data. We conclude by a series of numerical experiments that reflect these two scenarios and that allow us to analyze the possible impact of unknown calibration errors.
Primer on Compressive Sensing in marine acquisition
To obtain high resolution images of the Earth subsurface, marine seismic surveys require dense sampling that can become prohibitively expensive especially when time-lapse is of interest. To address this issue in seismic data acquisition, Hennenfent and Herrmann (2008), F. J. Herrmann (2010), Mansour et al. (2012), and Mosher et al. (2014) adapted ideas from Compressive Sensing (CS, Donoho, 2006; Candès et al., 2006), whereby cost of surveys depends on our ability to leverage certain inherent structure in seismic data rather than on the sample rate and size of the survey area. In seismic applications, adherence to three + one key principles of (distributed) CS are critical, namely we need to
(i) find a compressible representation, e.g. via transform-domain sparsity; (ii) design a physically realizable randomized subsampling scheme, which turns subsampling related artifacts into incoherent noise that is not compressible; (iii) restore densely sampled data by promoting structure—i.e., by mapping incoherent artifacts to coherent signal; (iv) exploit information shared amongst time-lapse vintages during the recovery, which allows us to maximally benefit from randomized sampling without insisting on replicating the surveys.
A physically realizable way to render marine acquisition more economically viable is to fire at random time-jittered compressed-in-time firing times (Wason and Herrmann, 2013). Depending on whether we work with dynamic towed arrays or static receivers (OBNs or OBCs), the variability in jittered firing times needs to be small or can be large, as illustrated in Figure 1.
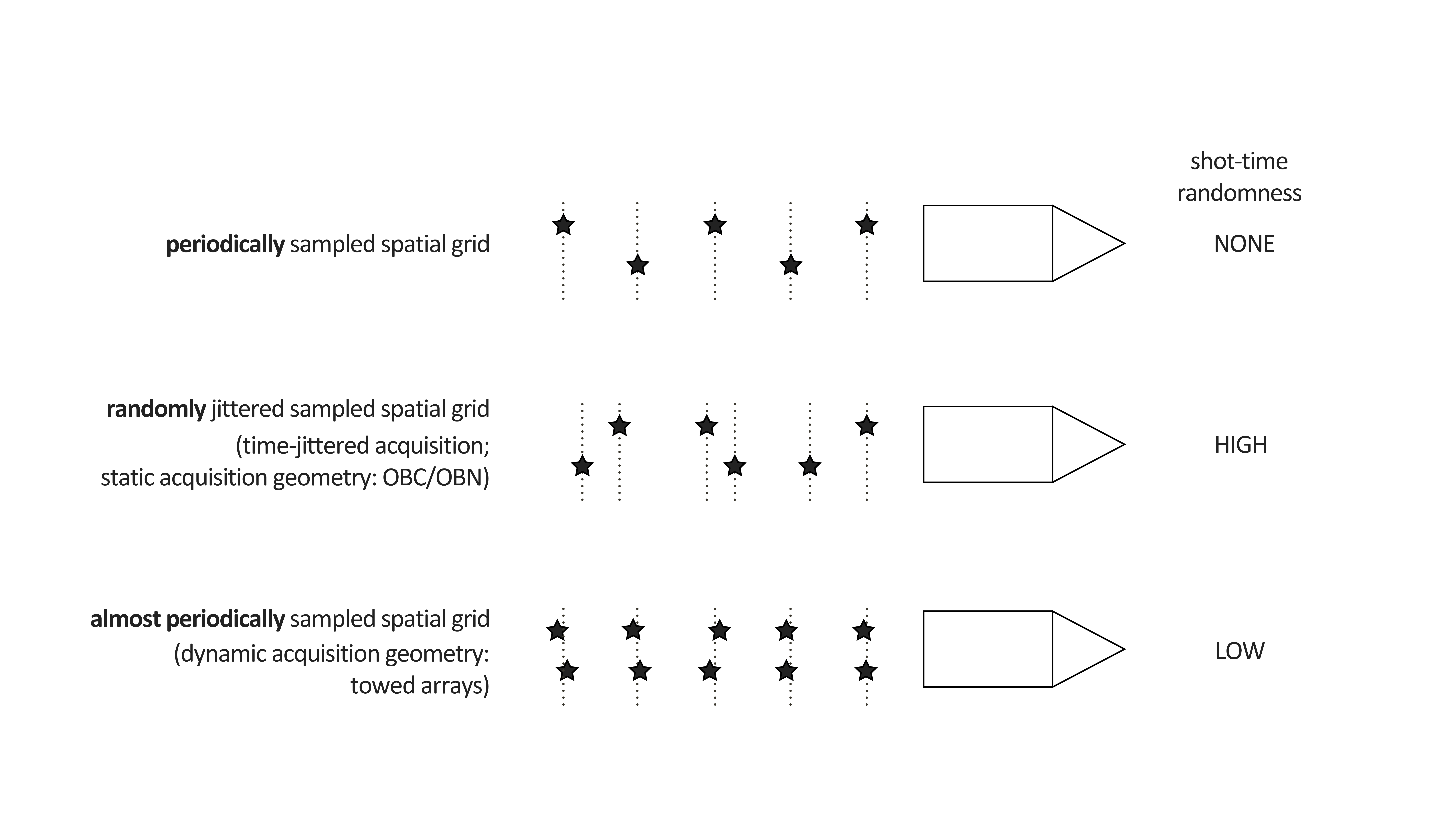
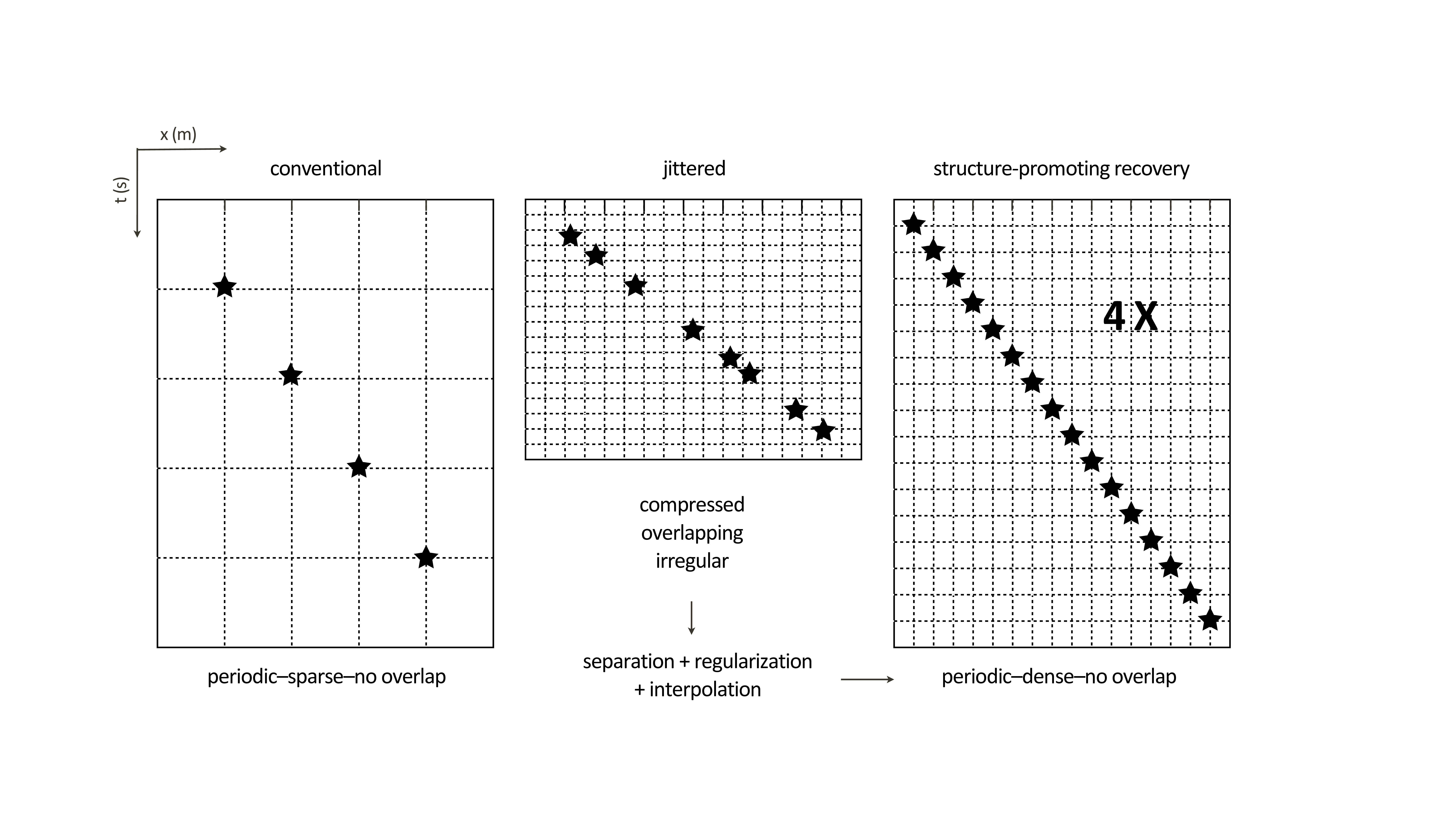
Here, we consider the more favorable case of large variability, for which good recovery results have been reported in the literature (Mansour et al., 2012; Wason and Herrmann, 2013) from surveys with overlapping shot records and coarse source sampling. Figure 2 illustrates how we compress the survey time and how we aim to reconstruct the wavefield onto a fine periodic grid with increased source sampling. Because we compressed the acquisition time and recover densely sampled data, our acquisition is more economic. For applications to full 3D at scale surveys with dynamic towed arrays, we refer the reader to our companion paper in this special issue.
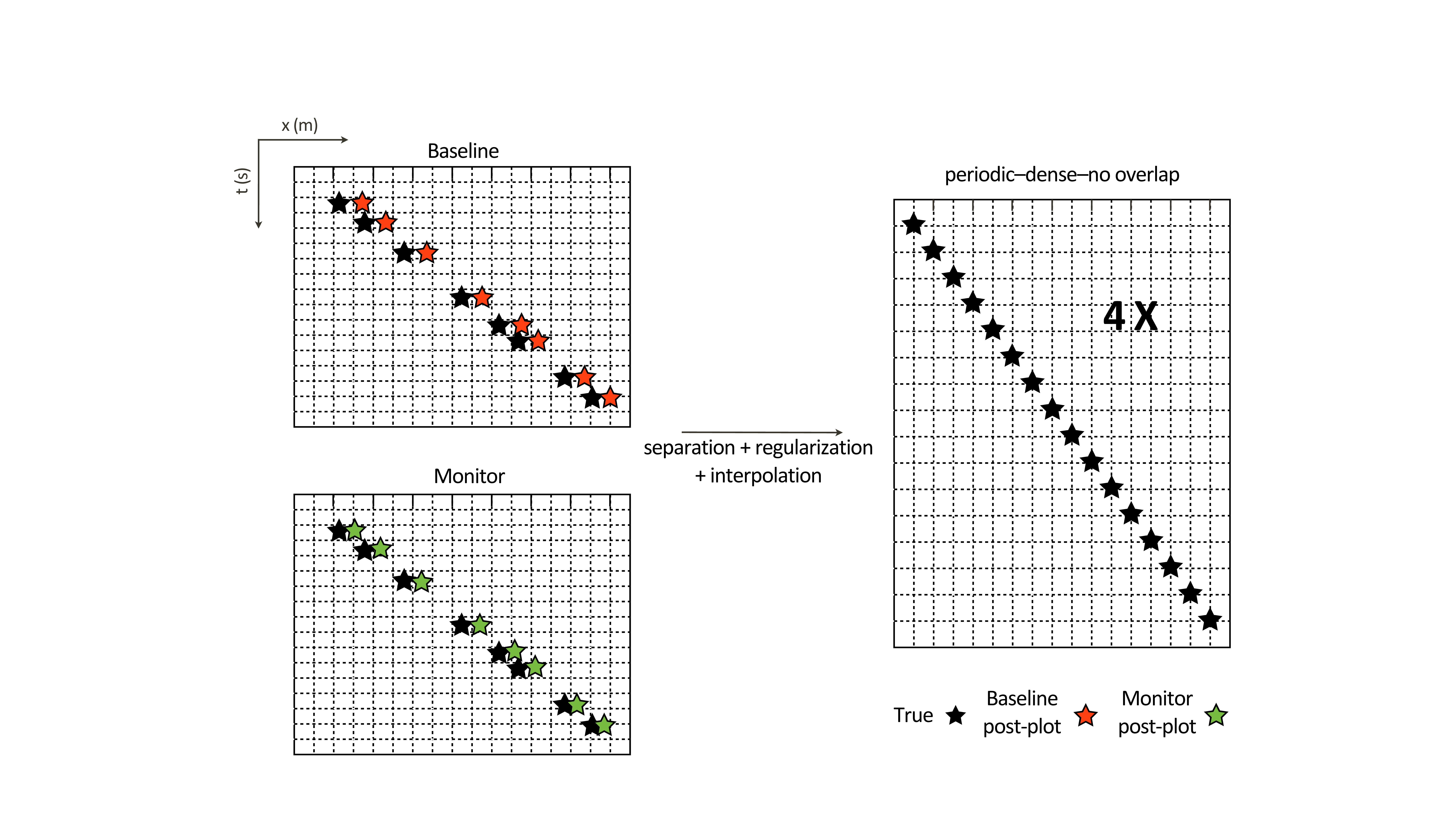
When provided with time-jittered surveys that are sufficiently calibrated, we can expect good recovery results (Oghenekohwo et al., 2017; Wason et al., 2017). However, as we mentioned in the Introduction, 3D and 4D seismic surveys are both susceptible to calibration errors, which are by definition unknown deviations between actual (true) and observed (post-plot) coordinates of sources/receivers. Figure 3 illustrates an example of our randomized and compressed time-lapse surveys where observed shot positions differ from the truth. The purpose of this work is to investigate the possible impact of these calibration errors on the recovered vintages and the time-lapse difference after reconstructing the surveys onto one and same fine periodic dense grid using our joint recovery model.
Methodology
Before we conduct experiments to quantify the degree of repeatability of randomized time-lapse surveys with calibration errors, let us first briefly introduce the joint recovery model and the NRMS. Without loss of generality, we consider the case of two time-lapse surveys only.
Compressive time-lapse acquisition
Let us denote baseline surveys with the index \(j=1\) and monitor surveys with the index \(j=2\). Following ideas from compressive sensing, we model data acquired with these two surveys by: \(\mathbf{y}_{j} = \mathbf{A}_{j}\mathbf{x}_{j}\ \text{for}\ j=\{1,2\},\) where \(\mathbf{y}_j\) are the usually observed randomly undersampled data for each survey. As described in Hennenfent and Herrmann (2008), F. J. Herrmann (2010), and Mansour et al. (2012), the matrices \(\mathbf{A}_j\) encapsulate specifics on the survey geometry for each vintage and the sparsifying transform used during the recovery. The task of the time-lapse seismic practitioner now is to recover the coefficient vectors \(\widetilde{\mathbf{x}}_j\)’s from sparse randomly undersampled \(\mathbf{y}_j\)’s from which estimates for densely sampled vintages \(\widetilde{\mathbf{d}}_j,\) that live on one and the same fine periodic grid can be derived. However, rather than recovering each vintage separately, by solving
\[ \begin{equation} \widetilde{\mathbf{x}}_j = \mathop{\rm arg\,min}_{\mathbf{x}_j}\|\mathbf{x}_j\|_1 \quad \text{subject to} \quad \mathbf{y}_j = \mathbf{A}_j\mathbf{x}_j, \,j=1,2, \label{eqirs} \end{equation} \]
we solve \[ \begin{equation} \widetilde{\mathbf{z}} = \mathop{\rm arg\,min}_{\mathbf{z}}\|\mathbf{z}\|_1 \quad \text{subject to} \quad \mathbf{y} = \mathbf{Az} \label{eqjrm} \end{equation} \] with
\[ \begin{equation} \begin{aligned} \underbrace{\begin{bmatrix} \mathbf{y}_1\\ \mathbf{y}_2\end{bmatrix}}_{\mathbf{y}} &= \underbrace{\begin{bmatrix} {\mathbf{A}_1} & \mathbf{A}_{1} & \mathbf{0} \\ {\mathbf{A}_{2} }& \mathbf{0} & \mathbf{A}_{2} \end{bmatrix}}_{\mathbf{A}} \underbrace{\begin{bmatrix} \mathbf{z}_0 \\ \mathbf{z}_1 \\ \mathbf{z}_2 \end{bmatrix}}_{\mathbf{z}}\\ \end{aligned} \label{jrmobs} \end{equation} \] instead. Compared to recovering the vintages separately as in Equation 1, the joint recovery model inverts for the coefficient vectors of the common component (\(\widetilde{\mathbf{z}}_0\)) and innovations (\(\widetilde{\mathbf{z}}_j\)) that encode the time-lapse. By construction, the common component of JRM benefits from sensing by both surveys (first column of \(\mathbf{A}\)). This can lead to markedly improved recoveries of densely periodically sampled vintages \(\widetilde{\mathbf{d}}_j\) derived from \(\widetilde{\mathbf{z}}_0\) and \(\widetilde{\mathbf{z}}_j\), without insisting on replicating the surveys as recently reported by Oghenekohwo et al. (2017) and Wason et al. (2017).
While the combination of randomized subsampling and the JRM offers unprecedented flexibility in cost-effective time-lapse acquisition, the recovery of densely sampled time-lapse data is built on the premise that reliable information on the actual acquisition geometry is available. This is to ensure that the modeling matrices (\(\mathbf{A}_j\)’s) accurately mimic the time-lapse measurements in the field. This reliance on accurate knowledge on the acquisition geometry raises some concern because in practice there will always be unknown calibration errors between observed and actual acquisition parameters.
To quantify the impact of these calibration errors, we will first consider the special case where \(\mathbf{x}_1 = \mathbf{x}_2\)— i.e., there is no time-lapse, but the randomized acquisitions differ (\(\mathbf{A}_1 \neq \mathbf{A}_2\)) and where there are differences between actual and observed post-plot acquisition parameters. In this situation and in the practical situation where time-lapse changes are localized, we still hope to attain high quality recovery and repeatability despite the presence of calibration errors.
NRMS — a measure for 4D repeatability
Common practice in time-lapse seismic processing is to measure the degree of repeatability of observed and processed data at each consecutive processing step (Ross et al., 1997; Harris and Veritas, 2005; Houck, 2007). This degree of repeatability measures the similarity between two time-lapse data sets, for example the recovered baseline (\(\widetilde{\mathbf{d}}_1\)) and monitor (\(\widetilde{\mathbf{d}}_2\)) surveys. As described by Kragh and Christie (2002), we quantify the degree of repeatability of the two vintages defined as the RMS of the difference between the two vintages divided by the average RMS of these two vintages—i.e., we have \[ \begin{equation*} \text{NRMS} (\widetilde{\mathbf{d}}_1,\widetilde{\mathbf{d}}_2) = \dfrac{ 200 \times \text{RMS}(\widetilde{\mathbf{d}}_1-\widetilde{\mathbf{d}}_2)}{\text{RMS}(\widetilde{\mathbf{d}}_1)+\text{RMS}(\widetilde{\mathbf{d}}_2)}, \end{equation*} \] with \[ \begin{equation*} \text{RMS}(\mathbf{d}) = \sqrt{\frac{\sum_{t=t_{1}}^{t_2}(\mathbf{d}[t])^{2}}{N}}, \end{equation*} \] where \(N\) is the number of samples in the interval \(t_{1}\) to \(t_{2}\) and \(\mathbf{d}[t]\) refers to a sample recorded at “time” \(t.\) By virtue of this definition, NRMS values range between \(0\) and \(200\) as percentages. The smaller the percentage, the more repeatable the vintages are. In practice, NRMS values are computed using seismic traces extracted from the data in a common time window and frequency band where there are no time-lapse changes.
Numerical experiments
To demonstrate the impact of calibration errors, we conduct a series of synthetic experiments involving non-replicated 2-D marine (ocean bottom cable) time-lapse surveys with unknown calibration errors only in the source positions. Recall that these errors are unknown deviations between the actual (true) and observed post-plot positions. For reference, we simulate idealized densely and regularly (periodic) sampled shots at \(12.5\)m interval on a realistic synthetic earth model with laterally varying densities and velocities. Our experiments compare a conventional dense survey, sampled irregularly with on average the same \(12.5\)m shot interval, and simultaneous source (randomly time-jittered) surveys acquired with our low-cost subsampling scheme (Wason and Herrmann, 2013). The latter entails a \(4\times\) speed-up in acquisition time resulting in overlapping shot records at irregular positions, sampled at an average coarse shot interval of \(50\)m. To mimic observed data with unknown calibration errors, we add random perturbations from a uniform distribution to the actual shot locations. As Table 1 shows, while we only need to regularize the conventional data since it is densely sampled, we process the low-cost data via shot separation, interpolation, and regularization. These experiments allow us to assess the repeatability quantitatively for the idealized case where the subsurface does not change and the practical situation where time-lapse changes are confined to a subset of the data.
| Conventional dense survey | Low-cost (\(4\times\) compressed) survey | |
|---|---|---|
| Shot geometry | Flip-flop irregular | 2 Sim. source |
| shot sampling | (time-jittered sources) | |
| Receiver geometry | OBC | OBC |
| Number of shots | 450 | 100 |
| Shot interval | 12.5m | 50m |
| Number of receivers | 450 | 450 |
| Receiver interval | 12.5m | 12.5m |
| Recovery (Processing) | Regularization | Shot separation, Interpolation, Regularization |
Idealized case — no time-lapse
To separate the possible impact of calibration errors from the time-lapse signal itself, we first consider the case where the earth model does not change between time-lapse surveys but where both the known survey parameters and unknown calibration errors differ. In this case, differences in the vintages can be attributed to differences in the surveys. For the densely but irregularly sampled data, we recover regularly sampled vintages via regularization of the observed data \(\mathbf{y}_j\) by directly computing the pseudo inverse \(\mathbf{A}_j^{\dagger}\mathbf{y}_j\), where the modeling matrices (\(\mathbf{A}_j\)’s) encapsulate the irregular shot geometry up to calibration errors that increase from \(0\) to \(50\%\) of the \(12.5\)m shot interval. We collect low-cost data by firing more often with jittering yielding fewer but irregular source locations that also contain calibration errors between \(0\) to \(50\%\) of the original \(12.5\)m shot interval. We recover these randomly subsampled datasets via independent and joint recovery (cf. Equation 1 and 2). We examine the quality of the recovered vintages in terms of S/N, and compute repeatability in terms of NRMS, for the conventional and low-cost acquisition as a function of the relative calibration errors. As we can see from Figure 4, recovery with JRM (third column) attains a relatively high S/N and greatly improved NRMS compared to the results from conventional acquisition (first column) and independent recovery (middle column), despite unknown calibration errors up to \(20\%\) of the dense shot interval.



Furthermore, to get more reliable estimates (mean and standard deviation) of the S/N and NRMS for increasing calibration errors, we repeat the experiments for \(10\) independent random realizations of the pairs of modeling matrices. Figures 5a and 5b show the results of this exercise, which allow us to make the following observations: (i) expectedly, calibrated surveys yield highest-quality vintages in terms of S/N compared to surveys that are not calibrated — this is because the modeling matrix for calibrated surveys correctly maps the observed data to the actual shot points whereas uncalibrated surveys violate this mapping; (ii) the quality of the vintages decreases gracefully for the low-cost compressed surveys with increasing calibration errors. Conversely, the quality of conventional irregular dense surveys decreases rapidly for increasing calibration errors — this is because errors arising from uncalibrated dense surveys behave like noise whose magnitude grows with the number of shots; (iii) for surveys with large (\(> 40\%\)) calibration errors, our low-cost sampling scheme with JRM is on par with the dense surveys regarding the recovery quality but relatively better in repeatability — the NRMS values for the low-cost acquisitions remain acceptable. These observations are consistent with our earlier findings on calibrated low-cost acquisitions (Oghenekohwo et al., 2017; Wason et al., 2017), again owing to making the common component shared by the the vintages explicit in the recovery.
Practical case — localized time-lapse
While the previous experiments demonstrate the impact of calibration errors on the vintages and the difference, we cannot guarantee that the effect of these errors will not propagate to the time-lapse signal in situations where the earth actually changes. Therefore, we conduct experiments on a synthetic time-lapse earth model with localized changes in both density and velocity. We compute the prestack localized 4D signal via subtraction of the two vintages after recovery towards a common grid. We now measure the recovery quality of the 4D signal and the repeatability of the vintages in presence of calibration errors, both for the conventional and low-cost acquisitions.
After data simulation and recovery as done previously, we perform repeatability analysis—compute the NRMS—outside the 4D signal window, and compute the S/N of the recovered prestack 4D signal only in the window where the 4D signal resides. We present the result of this experiment in Figures 5c and 5d. Despite the fact that the earth changes, the NRMS values behave more or less the same as in Figure 5b. This means that high degrees of repeatability are achievable with S/Ns that decrease gracefully compared to the conventional sampling and independent recovery. This experiment clearly shows that the uplift of costly dense sampling may be negated by the presence of relatively small (\(10\% \approx 1.25\) m) calibration errors.
Conclusions
Errors in acquisition parameters unbeknown to subsequent seismic data processing, including regularization and shot separation, can have detrimental effects on the quality and repeatability in particular when mapping time-lapse seismic surveys to a common densely sampled periodic grid. For the case of post-plot calibration errors in the source locations, we were able to demonstrate that high quality and highly repeatable vintages and time-lapse data are attainable in the presence of source position errors that are of order of \(20-25\%\) of the interpolated shot sample interval. As expected, high-cost densely sampled acquisitions may indeed lead to the best quality and repeatability in the absence of calibration errors. However, the quality and repeatability of these expensive densely sampled surveys decays very rapidly in the presence of even relatively small (\(10\%\) of the shot sample interval) calibration errors. Understandably, the quality and repeatability of four times cost-reduced compressive acquisitions is also affected by calibration errors but this deterioration is much more modest for vintages and time lapse data obtained with our joint recovery model. This result holds for both the idealized situation where the subsurface does not change and where differences in the vintages and time-lapse data are due to both differences in the surveys and (uncontrollable) calibration errors, or for the realistic situation where time-lapse changes in the subsurface are confined to subsets of the data. Either way, the performance of the joint recovery model for acquisitions with unknown calibration errors is remarkable and can be explained by the fact that our approach leverages information that is common amongst the vintages explicitly. With these observations, we are confident that economic time-lapse surveys with Compressive Sensing are indeed feasible and ready to be conducted in the field.
Acknowledgements
This research was carried out as part of the SINBAD II project with the support of the member organizations of the SINBAD Consortium.
Baron, D., Duarte, M. F., Wakin, M. B., Sarvotham, S., and Baraniuk, R. G., 2009, Distributed compressive sensing: CoRR, abs/0901.3403. Retrieved from http://arxiv.org/abs/0901.3403
Brown, G., and Paulsen, J., 2011, Improved marine 4D repeatability using an automated vessel, source and receiver positioning system: First Break, 29, 49–58.
Candès, E. J., Romberg, J., and Tao, T., 2006, Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information: IEEE Transactions on Information Theory, 52, 489–509.
Donoho, D. L., 2006, Compressed sensing: Information Theory, IEEE Transactions on, 52, 1289–1306.
Eggenberger, K., Christie, P., Manen, D.-J. van, and Vassallo, M., 2014, Multisensor streamer recording and its implications for time-lapse seismic and repeatability: The Leading Edge, 33, 150–162.
Eiken, O., Haugen, G. U., Schonewille, M., and Duijndam, A., 2003, A proven method for acquiring highly repeatable towed streamer seismic data: Geophysics, 68, 1303–1309.
Harris, P., and Veritas, D., 2005, Prestack repeatability of time-lapse seismic data: In SEG technical program expanded abstracts (Vol. 25, pp. 2410–2413).
Hennenfent, G., and Herrmann, F. J., 2008, Simply denoise: Wavefield reconstruction via jittered undersampling: Geophysics, 73, V19–V28.
Herrmann, F. J., 2010, Randomized sampling and sparsity: Getting more information from fewer samples: Geophysics, 75, WB173–WB187.
Hicks, E., Hoeber, H., Poole, G., and King, B., 2014, An efficient 4D processing flow for variable-depth streamer data: The Leading Edge, 33, 172–180.
Houck, R. T., 2007, Time-lapse seismic repeatability—How much is enough? The Leading Edge, 26, 828–834.
Kragh, E., and Christie, P., 2002, Seismic repeatability, normalized rms, and predictability: The Leading Edge, 21, 640–647.
Mansour, H., Wason, H., Lin, T. T., and Herrmann, F. J., 2012, Randomized marine acquisition with compressive sampling matrices: Geophysical Prospecting, 60, 648–662.
Mosher, C., Li, C., Morley, L., Ji, Y., Janiszewski, F., Olson, R., and Brewer, J., 2014, Increasing the efficiency of seismic data acquisition via compressive sensing: The Leading Edge, 33, 386–391.
Oghenekohwo, F., Wason, H., Esser, E., and Herrmann, F. J., 2017, Low-cost time-lapse seismic with distributed Compressive Sensing—Part 1: Exploiting common information among the vintages: Geophysics, 82, P1–P13.
Rickett, J., and Lumley, D., 2001, Cross-equalization data processing for time-lapse seismic reservoir monitoring: A case study from the gulf of mexico: Geophysics, 66, 1015–1025.
Ross, C. P., Altan, S., and others, 1997, Time-lapse seismic monitoring: Repeatability processing tests: In Offshore technology conference. Offshore Technology Conference.
Schisselé, E., Forgues, E., Echappé, J., Meunier, J., De Pellegars, O., and Hubans, C., 2009, Seismic repeatability–Is there a limit? In 71st eAGE conference & exhibition.
Wason, H., and Herrmann, F. J., 2013, Time-jittered ocean bottom seismic acquisition: In SEG technical program expanded abstracts 2013 (pp. 1–6). Society of Exploration Geophysicists.
Wason, H., Oghenekohwo, F., and Herrmann, F. J., 2017, Low-cost time-lapse seismic with distributed Compressive Sensing—Part 2: Impact on repeatability: Geophysics, 82, P15–P30.