 |
 |
 |
 | Bayesian wavefield separation by transform-domain sparsity
promotion |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Wang et. al.: Curvelet-based
Previous: Empirical choice of the
Discussion
As shown in our derivation, the Bayesian formulation in
Equation 5 leads to an optimization problem--i.e., the
minimization of
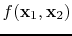 , which involves a
combined minimization of the weighted
, which involves a
combined minimization of the weighted 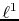 -norms of the
coefficient vectors, the
-norms of the
coefficient vectors, the 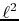 -misfit between the SRME-predicted
and estimated multiples, and the
-misfit between the SRME-predicted
and estimated multiples, and the 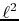 -misfit between the sum of
the estimated primaries and multiples and the observed total data.
From this interpretation, it is clear that our Bayesian formulation is
an extension of earlier work (Herrmann et al., 2007a) since our objective
function includes an additional term. This new term acts as a
safeguard by making sure that the estimated multiples remain
sufficiently close to the SRME-predicted multiples.The lower our
confidence is in the SRME-predicted multiples, the more emphasis
we place on the total data misfit. The case
-misfit between the sum of
the estimated primaries and multiples and the observed total data.
From this interpretation, it is clear that our Bayesian formulation is
an extension of earlier work (Herrmann et al., 2007a) since our objective
function includes an additional term. This new term acts as a
safeguard by making sure that the estimated multiples remain
sufficiently close to the SRME-predicted multiples.The lower our
confidence is in the SRME-predicted multiples, the more emphasis
we place on the total data misfit. The case
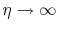 is
analogous to an absolute lack of confidence on the SRME-predicted
multiples, and thus includes a misfit concerning the total data
only. This limiting unrealistic assumption underlaid our earlier
formulation (Herrmann et al., 2007a). Away from this limit,
Equation 6 leads to solutions that are not only sparse,
but also produce estimated curvelet coefficients for the multiples
that are required to fit the SRME-predicted multiples. The relative
degrees of sparsity for the two signal components are
controlled by
is
analogous to an absolute lack of confidence on the SRME-predicted
multiples, and thus includes a misfit concerning the total data
only. This limiting unrealistic assumption underlaid our earlier
formulation (Herrmann et al., 2007a). Away from this limit,
Equation 6 leads to solutions that are not only sparse,
but also produce estimated curvelet coefficients for the multiples
that are required to fit the SRME-predicted multiples. The relative
degrees of sparsity for the two signal components are
controlled by 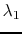 and
and 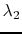 .
.
The performance of the presented separation algorithm depends on: (i)
the sparsity of the coherent signal components in the transform
domain: the sparser the two signal components, the smaller the chance
that the supports of the two curvelet coefficient vectors overlap;
(ii) the validity of the independence assumption, which is empirically
established in Herrmann et al. (2007a); (iii) the accuracy of the
SRME-predictions. Even though it was shown that curvelet-domain
separation is relatively insensitive to errors in the
SRME-predictions, significant amplitude errors (significant timing
errors are assumed absent) lead to a deterioration of the
separation. However, for smoothly varying amplitude errors, a remedy
for this situation has recently been proposed that is based on
introducing a secondary curvelet-domain matched filter
(Herrmann et al., 2007b).
 |
 |
 |
 | Bayesian wavefield separation by transform-domain sparsity
promotion |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Wang et. al.: Curvelet-based
Previous: Empirical choice of the
2008-03-13