 |
 |
 |
 | Bayesian wavefield separation by transform-domain sparsity
promotion |  |
![[pdf]](icons/pdf.png) |
Next: Discussion
Up: Theory
Previous: The separation algorithm
Empirical choice of the weights
In practice, the appropriate choice of the weights
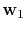 and
and
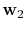 proves important. Motivated by empirical findings
(Herrmann et al., 2007a), we choose the weights using the SRME
predictions for the two signal components: we set
proves important. Motivated by empirical findings
(Herrmann et al., 2007a), we choose the weights using the SRME
predictions for the two signal components: we set
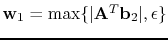 and
and
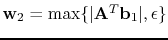 with the
operations taken elementwise. Here,
with the
operations taken elementwise. Here,
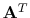 is the forward
curvelet transform (the discrete curvelet transform based on wrapping
is a tight frame, so the transpose of this transform is its inverse)
and
is the forward
curvelet transform (the discrete curvelet transform based on wrapping
is a tight frame, so the transpose of this transform is its inverse)
and 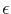 a noise dependent constant. This choice of weights
guarantees that the weights are strictly positive, thus the algorithm
converges. Furthermore, such a choice makes it less likely that the
optimization algorithm produces large curvelet coefficients for the
primaries at entries in the curvelet vector that exhibit large
coefficients for the predicted multiples, and vice versa.
a noise dependent constant. This choice of weights
guarantees that the weights are strictly positive, thus the algorithm
converges. Furthermore, such a choice makes it less likely that the
optimization algorithm produces large curvelet coefficients for the
primaries at entries in the curvelet vector that exhibit large
coefficients for the predicted multiples, and vice versa.
Remark: Within the Bayesian context, this particular choice
breaks the assumption that the curvelet coefficients of the primaries
and multiples are independent. However, our estimator can still be
interpreted as Bayesian with a posterior probability of the form given
in Equation 5
with the weights defined as mentioned above.
 |
 |
 |
 | Bayesian wavefield separation by transform-domain sparsity
promotion |  |
![[pdf]](icons/pdf.png) |
Next: Discussion
Up: Theory
Previous: The separation algorithm
2008-03-13