 |
 |
 |
 | Adaptive curvelet-domain primary-multiple separation |  |
![[pdf]](icons/pdf.png) |
Next: Curvelet-domain matched filtering
Up: Theory
Previous: Theory
The forward model
Without the wavelet and source directivity, the predicted multiples
can be regarded as some scaled (along the time and receiver or offset
axes) version of the true multiples. Mathematically, this
nonstationary 'scaling' can be represented by a pseudo-differential
operator. For our application, this operator acts on shot records or
on common-offset panels and applies a location, frequency and
dip-dependent zero-phase scaling. By applying a matrix-vector
multiplication to the predicted multiples, this operator models the
true multiples in the data, i.e.,
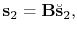 |
(1) |
where
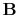 is a full positive-definite matrix, implementing
the action of the pseudo-differential operator and
is a full positive-definite matrix, implementing
the action of the pseudo-differential operator and
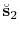 represents the predicted multiples, calculated with single-windowed
convolutional matched filtering. Relating the predicted multiples to
the true multiples offers flexibility to model amplitude
mismatches. Note, however, that this model cannot incorporate
kinematic shifts, since pseudo-differential operators are unable to
move wavefronts.
represents the predicted multiples, calculated with single-windowed
convolutional matched filtering. Relating the predicted multiples to
the true multiples offers flexibility to model amplitude
mismatches. Note, however, that this model cannot incorporate
kinematic shifts, since pseudo-differential operators are unable to
move wavefronts.
By compensating for the source wavelet and directivity, via a
conventional local matched-filtering procedure, the
pseudo-differential operator becomes zero order and permits a diagonal
curvelet-domain decomposition (Herrmann et al., 2007c),
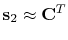 diag diag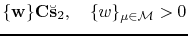 |
(2) |
with
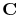 the 2D discrete curvelet transform (see
e.g. Candes et al., 2006; Hennenfent and Herrmann, 2006) and
the 2D discrete curvelet transform (see
e.g. Candes et al., 2006; Hennenfent and Herrmann, 2006) and
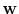 the
curvelet-domain scaling vector and
the
curvelet-domain scaling vector and
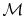 the index set of
curvelet coefficients. Since we are using the curvelet transform based
on wrapping, which is a tight frame, we have
the index set of
curvelet coefficients. Since we are using the curvelet transform based
on wrapping, which is a tight frame, we have
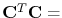
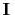 and the transpose, denoted by the symbol
and the transpose, denoted by the symbol
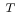 , equals the pseudo inverse.
, equals the pseudo inverse.
In this approximate forward model, for which precise theoretical error
estimates exist (Herrmann et al., 2007c), the predicted multiples are
linked to the actual multiples by a simple curvelet-domain scaling.
This curvelet-domain scaling applies a location, scale and dip
dependent amplitude correction. Since the matrix
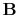 is positive-definite, the entries in the scaling vector,
is positive-definite, the entries in the scaling vector,
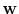 ,
are positive. This approximate formulation of the forward model forms
the basis for our curvelet-domain matched filter.
,
are positive. This approximate formulation of the forward model forms
the basis for our curvelet-domain matched filter.
 |
 |
 |
 | Adaptive curvelet-domain primary-multiple separation |  |
![[pdf]](icons/pdf.png) |
Next: Curvelet-domain matched filtering
Up: Theory
Previous: Theory
2008-01-18
![]() is positive-definite, the entries in the scaling vector,
is positive-definite, the entries in the scaling vector,
![]() ,
are positive. This approximate formulation of the forward model forms
the basis for our curvelet-domain matched filter.
,
are positive. This approximate formulation of the forward model forms
the basis for our curvelet-domain matched filter.