Simply denoise: wavefield reconstruction via jittered undersampling

Motivation

Recent results in Information Theory and Approximation Theory established that a signal can be recovered exactly from (severely) undersampled data points provided that 1) the signal exhibits sparsity in a known transform domain, 2) the artifacts introduced by undersampling look like incoherent random noise in the sparsifying domain, and 3) a data-consistent sparsity-promoting procedure is used for the recovery. It is possible to build an intuitive understanding of these theoretical results, termed Compressive Sampling (CS - Candès and Romberg, 2006; Donoho, 2006; Candès et al., 2006), by considering a simple example.

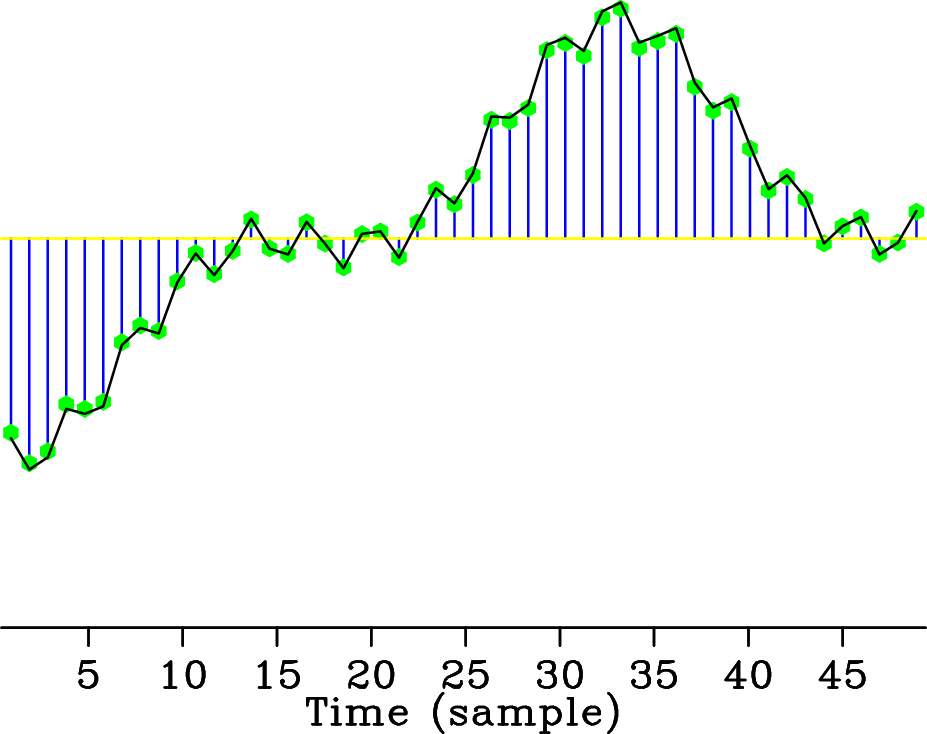
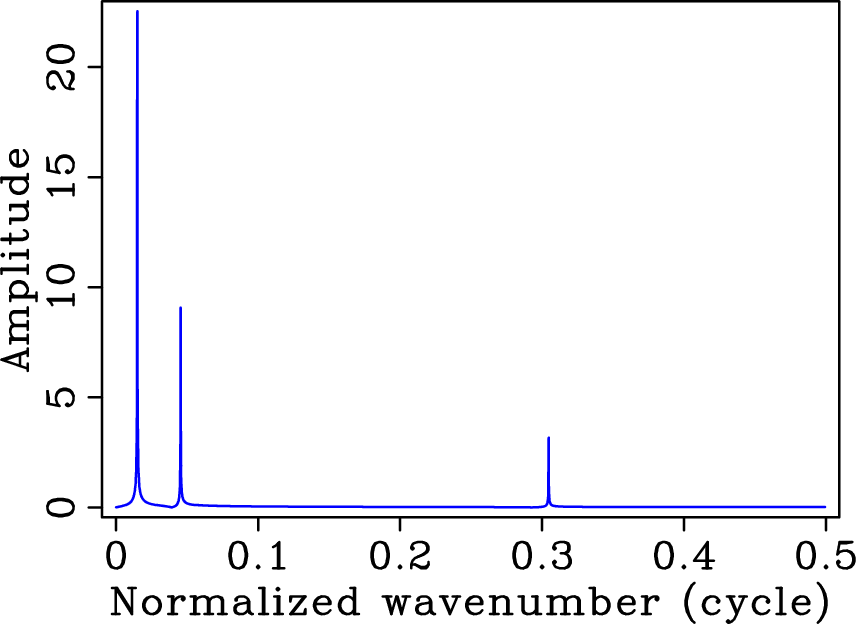
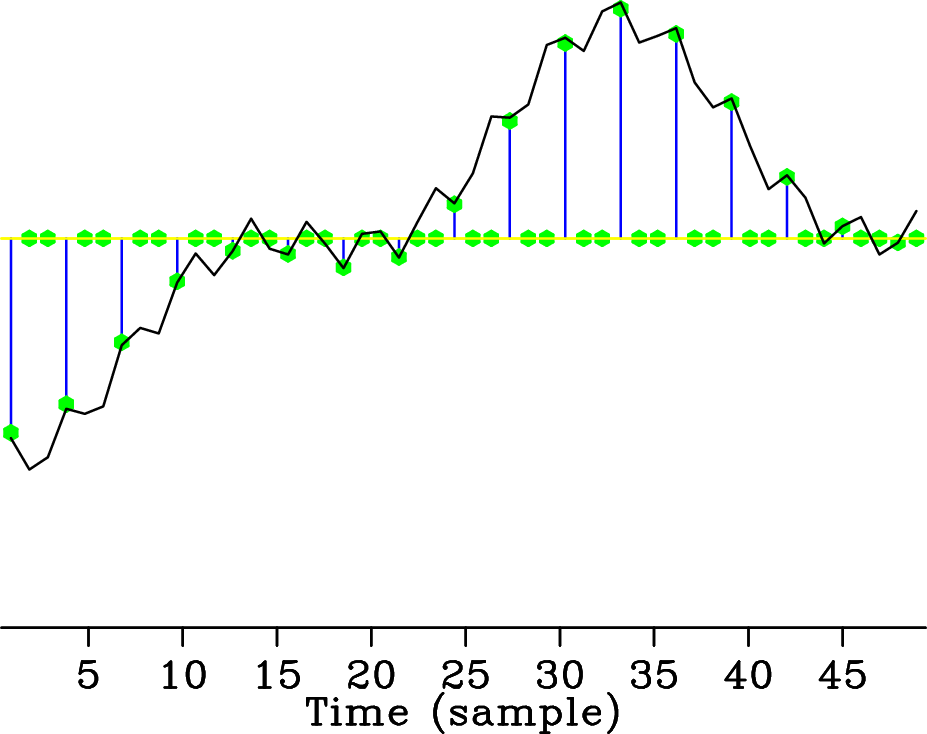
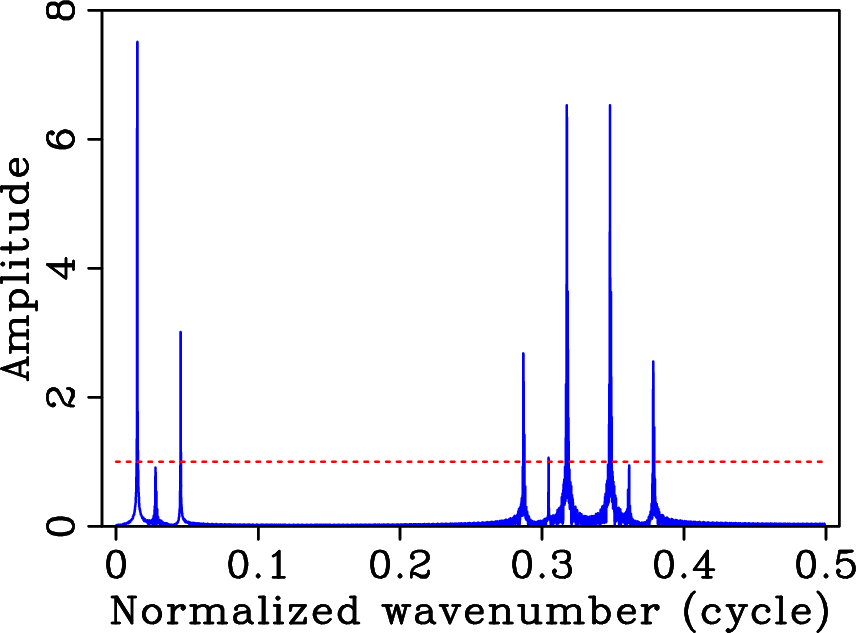
Figure 1(a) shows the superposition of three cosine functions. This signal is sparse in the Fourier domain (condition 1) and is regularly sampled above Nyquist rate. Its amplitude spectrum is plotted in Figure 1(b). When the signal is randomly three-fold undersampled according to a discrete uniform distribution as in Figure 1(c), its amplitude spectrum, plotted in Figure 1(d), is corrupted by artifacts (condition 2) that look like additive incoherent random noise. In this case, the significant coefficients of the to-be-recovered signal remain above the ``noise'' level. These coefficients can be detected with a denoising technique that promotes sparsity, e.g., nonlinear thresholding (dashed line in Figures 1(d) and 1(f)), and exactly recovered by an amplitude-matching procedure to fit the acquired data (condition 3). This experiment illustrates a favorable recovery from severely undersampled data points of a signal that is sparse in the Fourier domain.

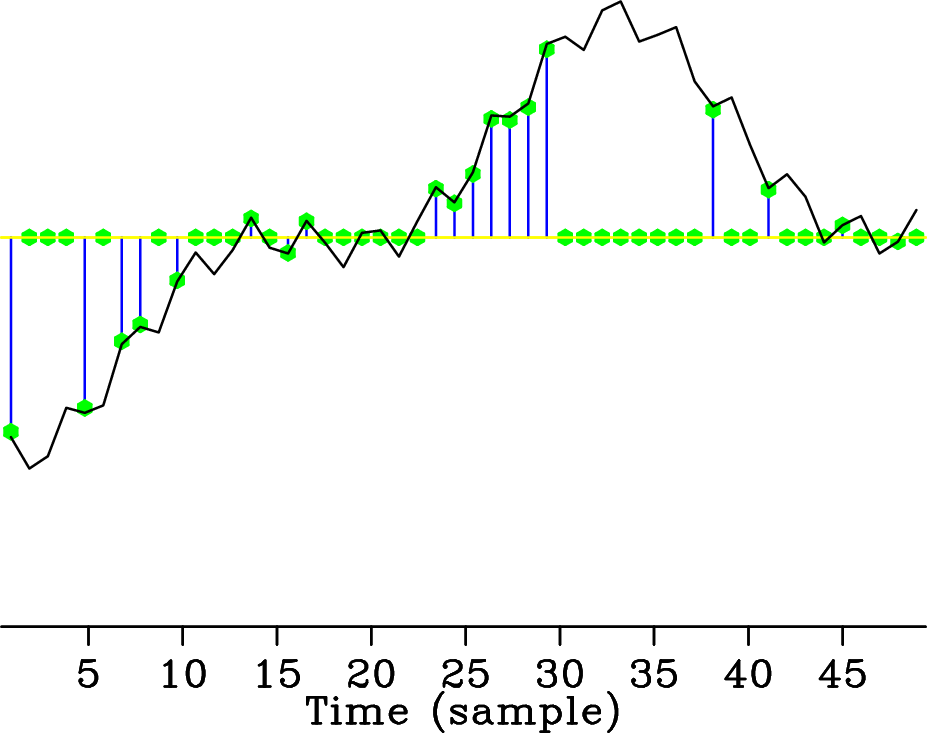
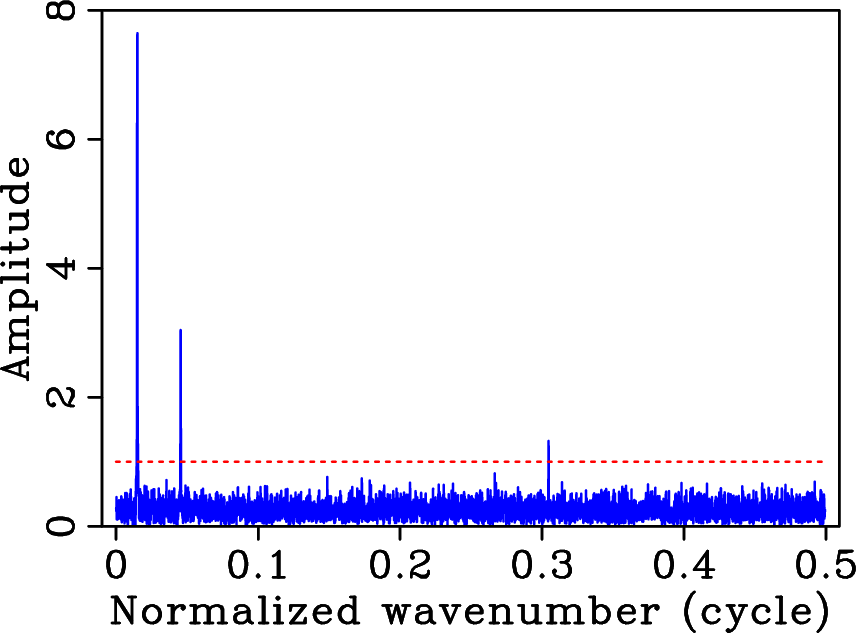
When the original signal is regularly three-fold undersampled (Figure 1(e)), the undersampling artifacts coherently interfere, giving rise to well-known aliases that look like the original signal components (Figure 1(f)). In this case, the above sparsity-promoting recovery scheme may fail because the to-be-recovered signal components and the aliases are both sparse in the Fourier domain. This example suggests that random undersampling according to a discrete uniform distribution is more favorable than regular undersampling for reconstruction algorithms that promote sparsity in the Fourier domain. In general terms, the above observations hint at undersampling schemes that lead to more favorable recovery conditions. Within the field of CS, significant advances have been made regarding the main ingredients that go into the design of an undersampling scheme that favors sparsity-promoting recovery. In this paper, we draw on these results to design a new coarse spatial sampling scheme for seismic data.

model,spec,IRREG,specIRREG,REG,specREG
Figure 1. Different (under)sampling schemes and their imprint in the Fourier domain for a signal that is the superposition of three cosine functions. Signal (a) regularly sampled above Nyquist rate, (c) randomly three-fold undersampled according to a discrete uniform distribution, and (e) regularly three-fold undersampled. The respective amplitude spectra are plotted in (b), (d) and (f). Unlike aliases, the undersampling artifacts due to random undersampling can easily be removed using a standard denoising technique promoting sparsity, e.g., nonlinear thresholding (dashed line), effectively recovering the original signal.

Simply denoise: wavefield reconstruction via jittered undersampling