Wavefield recovery with limited-subspace weighted matrix factorizations

Introduction

Seismic data acquisition plays a key role in the initial phase of oil & gas exploration. It also represents a significant budget item for monitoring of carbon sequestration. For these reasons, it is a challenge to come up with new acquisition methodologies that improve acquisition productivity (Mosher et al., 2014) without sacrificing data quality. Randomized acquisition according to the principles of compressive sensing (Herrmann et al., 2012) in combination with large-scale wavefield reconstruction algorithms (Kumar et al., 2015) has proven a viable tool to improve the acquisition productivity both in marine and land seismic settings.

So far, many of the employed approached of wavefield reconstruction are based transform-domain sparsity, which is deigned to explore local smoothness typically in small windows in up to five dimensions. While these approaches have been applied successfully on production data, they do no exploit redundancies present in the data over long distances. Recovery techniques based on low-rank matrix factorizations (Kumar et al., 2015) do not suffer from this shortcoming because this method works with monochromatic frequency slices that contain data from the complete survey instead of working within small windows limiting the apperture. By organizing the data in the appropriate domain, e.g. midpoint-offset domain for seismic lines, monochromatic frequency slices permit approximations in low-rank form, which can be used to recover fully sample wavefields from subsampled data.

While low-rank factorizations have been employed successfully for low and midrange frequencies, their performance deteriorates at high frequencies because monochromatic frequency slices can no longer be approximated accurately by low-rank factorizations. In this work, we overcome this problem by using the fact that factorizations at neighboring frequencies live in close-by subspaces. As described in early work by Aravkin et al. (2013); Eftekhari et al. (2018), this property can be exploited by introducing matrix weights defined in terms of factorizations of near-by frequency slices. Recent work by Zhang et al. (2019) took this initial a step further by proposing a recursive approach where factorizations of frequency slices at lower frequencies are used as weight for factorizations at the higher frequencies starting at the low frequencies and working its way up.

While this approach has had some success (see e.g. Zhang et al. (2019)), there is challenge related to the fact that high frequencies require higher rank factorizations and this can lead to overfitting when using this higher rank throughout. We avoid this overfitting, by adapting the rank of the weighting matrices such that overfitting is avoided. We do this by actively limiting the row and column subspaces of the weight matrices. Because we avoid overfitting, we are able to further improve the wavefield recovery. We also introduce an alternative formulation where the weight matrices are moved from the constraint, as in Kumar et al. (2015), to the data misfit objective, which leads to a significant improvement (\(20\) to \(25\) times speedup) computational efficiency.

We organize our paper as follows. First, we review the recursively weighted wavefield recovery via matrix factorization including the new formulation where the weight appear in the data misfit term. Next, we discuss how to limit the subspace of our weighted matrix factorizations. We conclude by demonstrating our approach on a field data example from the Gulf of Suez, which shows improved recovery quality compared to conventional recursively weighted matrix completion.

Methodology

We start by introducing wavefield reconstruction via weighted matrix factorization. To improve computational efficiency, we move the weight matrices to the data misfit term so we no longer have to carry out numerically expensive weighted projections as in (Aravkin et al., 2013). Aside from allowing for a much more computationally efficient implementation, this alternative formulation also forms the basis for our limited-subspace approach designed to prevent overfitting at the low frequencies.

Weighted low-rank matrix factorization

Our proposed extension to wavefield reconstruction via recursively weighted matrix factorization derives from earlier work by Kumar et al. (2015), Aravkin et al. (2013), and Zhang et al. (2019), where we solve \[ \begin{equation} \begin{aligned} & \minim_{\vector{X}_i} \quad \|\vector{Q}\vector{X}_i\vector{W}\|_*\\ & \text{subject to} \quad \|\mathcal{A}(\vector{X}_i) - \vector{b}_i\|_2 \leq \tau \end{aligned} \label{eqWlrmf} \end{equation} \] to within a noise-level dependent data misfit tolerance \(\tau\). In this expression, the matrix \(\vector{X}_i\) corresponds to a monochromatic frequency slice in the midpoint/offset domain (in case of \(2\)D) at the \(i\mathrm{th}\) frequency (\(i \in [1, \cdots , n_f]\) with with \(n_f\) the number of frequencies).

During the wavefield recovery, fully sampled frequency slices are represented by the complex valued matrix, \(\vector{X} \in \mathbb{C}^{n_f \times n_m \times n_h}\) where \(n_m\) is the number of midpoints and \(n_h\) the number of offsets. The symbol \(\mathcal{A}(\cdot)\) stands for the subsampling operator, which collects monochromatic data at the observed source/receiver combinations into the vector \(\vector{b}_i\). Given these observations, we solve for the fully sampled \(\mathbf{X}_i\) for each frequency by minimizing equation \(\ref{eqWlrmf}\) with weight matrices \(\vector{Q}\) and \(\vector{W}\) given by \[ \begin{equation} \vector{Q} = {w}_{1}\vector{U}\vector{U}^H + \vector{U}^\perp \vector{U}^{{\perp}{H}} \label{eqprojl} \end{equation} \] and \[ \begin{equation} \vector{W} = {w}_{2}\vector{V}\vector{V}^H + \vector{V}^\perp \vector{V}^{{\perp}{H}}. \label{eqprojr} \end{equation} \] In these expressions for the weight matrices, the \(\vector{U} \in \mathbb{C}^{n_m \times r}\) and \(\vector{V}\in \mathbb{C}^{n_h \times r}\) are the column and row subspaces that derive from the low-rank factorization of the nearby frequency slice. \(\vector{U}\) and \(\vector{V}\) have orthonormal columns that span top column and row subspaces of nearby frequency slice. Because these weight matrices include information on the subspaces of the current factorization, they serves as prior information aiding the wavefield recovery via the weighted nuclear norm minimization (denoted by \(\|\mathbf{QXW}\|_\ast=\sum_{j=1}^{r}\sigma_j\) with \(\sigma_j\) the \(j^{\text{th}}\) singular value). Depending on whether we have confidence in the fact that the neighboring frequency slice has an overlapping subspace, we chose the weights \(w_1\) and \(w_2\) close to \(0\) if we have confidence and close to \(1\) if we do not.

While the above weighted formulation has resulted in major improvements in the recovery when reliable information on a neighboring frequency slice is available (Kumar et al., 2015, Aravkin et al. (2013), and Zhang et al. (2019)), the minimization in equation \(\ref{eqWlrmf}\) is complicated by the presence of the weighting matrices in the nuclear norm objective. As a result, the minimization becomes computationally expensive. To avoid this complication, we replace the optimization variable by \(\vector{\bar{X}}_{i} = \vector{Q}\vector{X}_i\vector{W}\), and rewrite equation \(\ref{eqWlrmf}\) as \[ \begin{equation} \begin{aligned} & \minim_{\vector{\bar{X}}_i} \quad \|\vector{\bar{X}}_i\|_* \\ & \text{subject to} \quad \|\mathcal{A}({\vector{Q}^{-1}}\vector{\bar{X}}_i{\vector{W}^{-1}}) - \vector{b}_i\|_2 \leq \tau \end{aligned} \label{eqWlrmfv2} \end{equation} \] where the modified weighting matrices \[ \begin{equation} {\vector{Q}^{-1}} = \frac{1}{w_1} \vector{U}\vector{U}^H + \vector{U}^\perp \vector{U}^{{\perp}{H}} \label{eqWrow} \end{equation} \] and \[ \begin{equation} {\vector{W}^{-1}} = \frac{1}{w_2} \vector{V}\vector{V}^H + \vector{V}^\perp \vector{V}^{{\perp}{H}} \label{eqWcol} \end{equation} \] are moved from the objective to the data misfit constraint. To reflect that we changed the problem, we introduced barred quantities from which the solution original solution can be readily computed—i.e., we recover the solution \(\vector{X}_i=\vector{Q}^{-1}\vector{\bar{X}}_i\vector{W}^{-1}\) since \(\vector{\bar{X}}_i=\vector{Q}\vector{X}_i\vector{W}\) solves the above optimization problem. Compared to equation \(\ref{eqWlrmf}\), this new formulation does not require nuclear norm projections onto weighted matrices while its solution is equivalent to equation \(\ref{eqWlrmf}\).

Like the original formulation, our new formulation lends also itself to be cast into a low-rank (\(r\ll \max(n_m,n_h)\)) factorized form so that expensive SVDs are avoided in the nuclear norm. After factorization our wavefield reconstruction involves \[ \begin{equation} \begin{aligned} & \minim_{\vector{\bar L}_i, \vector{\bar R}_i} \quad \frac{1}{2} {\left\| \begin{bmatrix} \vector{\bar L}_i \\ \vector{\bar R}_i \end{bmatrix} \right\|}_F^2 \\ & \text{subject to} \quad \|\mathcal{A}{({\vector{Q}^{-1}} \vector{\bar L}_i \vector{\bar R}_i^{H} {\vector{W}^{-1}})} - \vector{b}_i\|_{2} \leq \epsilon, \end{aligned} \label{eqwlrf} \end{equation} \] where the symbol \(^{H}\) denotes the Hermitian transpose and \(\|\cdot\|_F\) is the Frobenius norm (2-norm of the vectorized matrix) (Kumar et al., 2015; Aravkin et al., 2013; Zhang et al., 2019). Compared to the original representation for frequency slices, the above factored form is compressed since it entails the low-rank pair \(\{\mathbf{\bar L}_i,\,\mathbf{\bar R}_i\}\) ,where \(\vector{\bar{X}}_i=\vector{\bar L}_i \vector{\bar R}_i^{H}\), and does not rely on storage and manipulation of the original and dense optimization variable \(\mathbf{X}_i\) or \(\mathbf{\bar X}_i\). Despite gains in computation, because of the factored form and redefined data misfit term, challenges remain with recursive weighted matrix factorizations (Zhang et al., 2019) at the high frequencies and as we will show these have to do with overfitting.

Limited subspace weighted implementation

To reduce approximation errors at the high frequencies, we can increase the rank of the factorization throughout. While increasing the rank leads to better approximations at the high frequencies adapting this higher rank at the lower frequencies can lead to overfitting. The resulting poor reconstructions at the lower frequencies can in turn have a detrimental effect on the reconstruction at higher frequencies, which information from the lower frequencies as the recursive algorithm sweeps from the low to the high frequencies.

By choosing the rank for the limited subspace, we reduce the size of the subspaces of the weight matrices to prevent overfitting at the lower frequencies. In equations \(\ref{eqprojl}\), \(\ref{eqprojr}\), \(\ref{eqWrow}\) and \(\ref{eqWcol}\), we notice that the size of the weight matrices \(\vector{Q}\) and \(\vector{W}\) are independent of rank \(r\). Therefore, we can use a limited subspace to remove the influence of overfitting and get better results.

By limited subspace, we mean that at a given frequency slice, instead of using a rank \(r\) for row and column subspaces \(\vector{U}\) and \(\vector{V}\) respectively, we can use a lower rank \(r_s\). In this way, we can choose higher rank \(r\) to reconstruct each frequency but use lower rank \(r_s\) to construct the weight matrices (\(\vector{Q}\) and \(\vector{W}\)). By choosing smaller rank for the subspaces, we mitigate the negative influence of overfitting. Therefore, in the limited-subspace method, we are free to choose smaller values for the \(r_s\) for each frequency slice and higher values for the rank \(r\) for the factorization itself (not for the weights) for each frequency.

Numerical Experiments

To demonstrate the advocacy of the proposed method, we use \(2\)D field seismic data acquired in the Gulf of Suez with number of sources, \({N}_{s}=355\), and number of receivers, \({N}_{r}=355\). The total number of time samples in this dataset is \({N}_{t}=1024\) and the sampling interval is \(0.004\, \mathrm{s}\). We use a jittered subsampling (Herrmann and Hennenfent, 2008) mask to remove \(75 \%\) of the sources to obtain the subsampled data. When data is organized in the midpoint-offset domain, we know that randomized jittered subsampling method breaks the inherent low-rank property of seismic data while controlling the largest gap size of the subsampled data (Herrmann and Hennenfent, 2008). Controlling largest gap is important because very large gaps are not suitable for wavefield reconstruction using sparsity-promotion or low-rank matrix completion. We use the weighted method as described by Zhang et al. (2019) to reconstruct frequency slices starting at \(10\, \mathrm{Hz}\) and working our way up to \(70\, \mathrm{Hz}\). We use constant rank across all the frequencies for weight matrices and matrix factorization. We base these choices for \(r_s<r\) on visual inspection of the recovered frequency slices. To avoid overfitting at lower frequencies we select rank \(r_s\) of the limited subspace constant across all the frequencies. And to better approximation of higher frequencies we choose higher rank \(r\) across all the frequencies. Combination of higher rank for matrix factorization and smaller rank for limited subspace avoid the risk of overfitting and at the same time improves the data reconstruction quality.

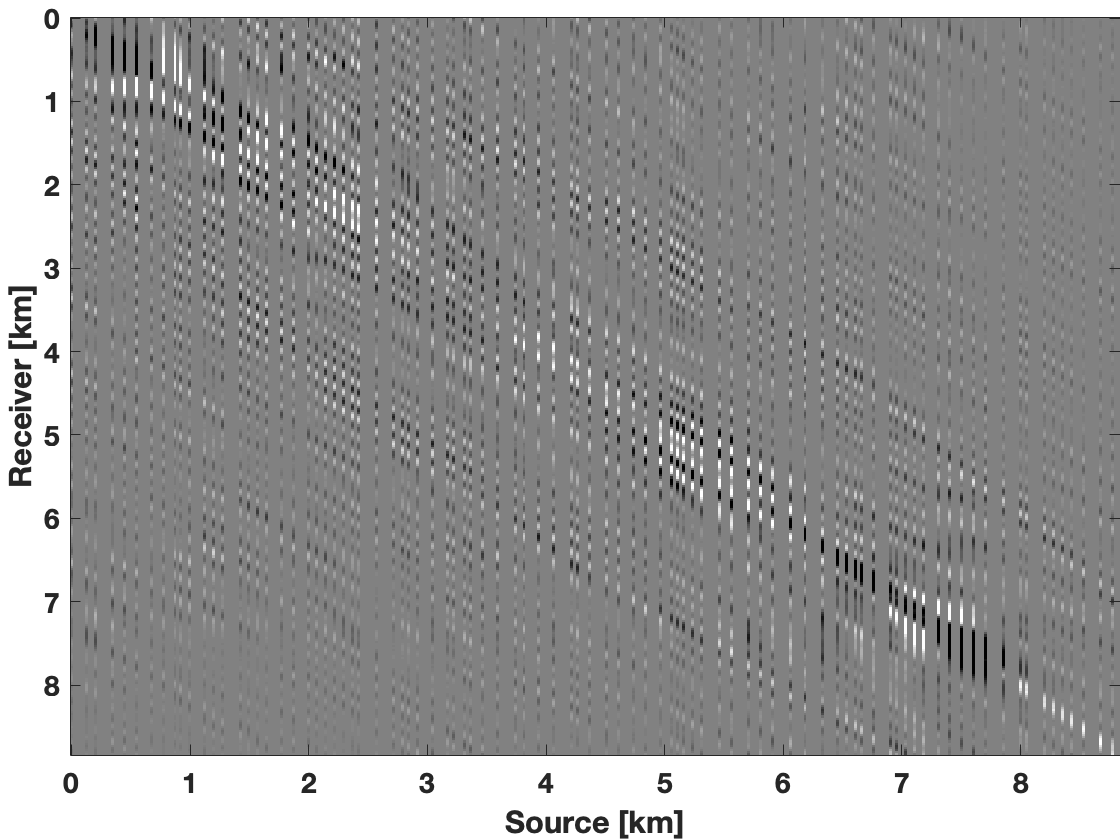
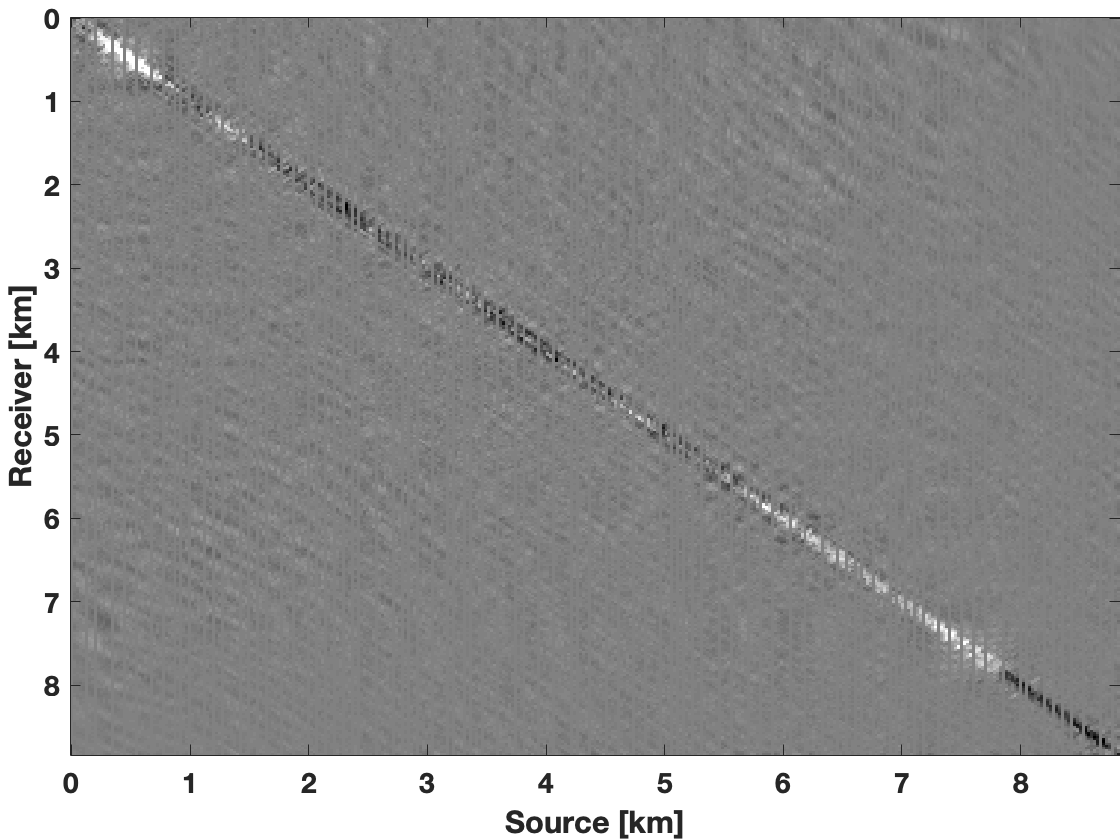
To demonstrate that the limited-subspace recursively weighted method gives improved results compared to conventional recursively weighted method (Zhang et al., 2019), we first show results in the frequency domain. For each frequency slice, we perform \(150\) iterations for both the methods. For the limited-subspace weighted method, we use rank \(r = 85\) and limited subspace rank of \(r_s = 25\). For comparison with the conventional weighted method, we perform two experiments with a fixed high rank of \(r=85\) and lower rank of \(r=25\). We choose lower rank for conventional weighted method to show that smaller rank itself is not sufficient for significant improvement in data reconstruction at higher frequencies. On the other hand we choose higher rank of 85 for conventional weighted method to show that higher rank is alone not sufficient to improve the quality of reconstructed data at higher frequencies because of the overfitting at lower frequencies. We show reconstruction results for a frequency slice at \(22\, \mathrm{Hz}\) in Figure 1. Due to overfiting, the conventional method with rank \(r=85\) gives a reconstruction with a smaller S/R of \(13.09\, \mathrm{dB}\) compared to the wavefield reconstruction (Figures 1c and 1d) obtained with the smaller rank \(r=25\) for which we get S/R of \(15.50\, \mathrm{dB}\) (Figures 1e and 1f). We get S/R of \(19.52\, \mathrm{dB}\) for the reconstructed data (Figures 1g) using the limited-subspace weighted method. Figure 1h shows the data residual with respect to the ground truth (Figure 1a). Clearly, our limited-subspace weighted method outperforms the conventional weighted method in terms of improved quality of reconstructed data.

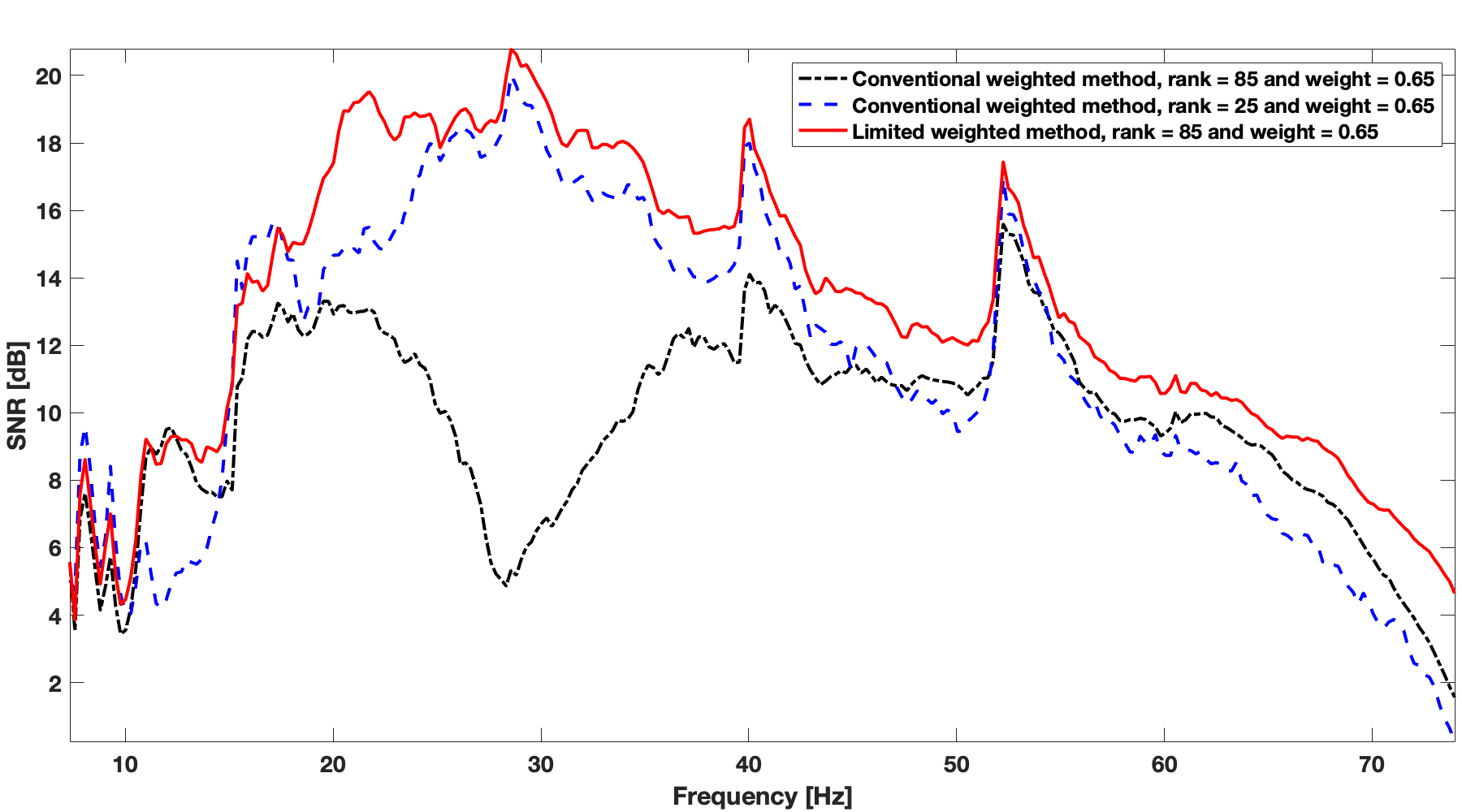
To further compare our limited-subspace method with the original method, we repeat wavefield reconstructions over a range of frequencies \(7-74\, \mathrm{Hz}\). In Figure 2, we show the comparison of the S/R’s across the whole frequency range. As expected, we observe that limited-subspace weighted method (red line in Figure 2) outperforms conventional weighted method for both ranks of \(25\) (blue line in Figure 2) and \(85\) (black line in Figure 2) for most of the frequencies. This is because of using limited subspace we avoid risk of overfitting at lower frequencies and hence get improvement in quality of reconstructed data.

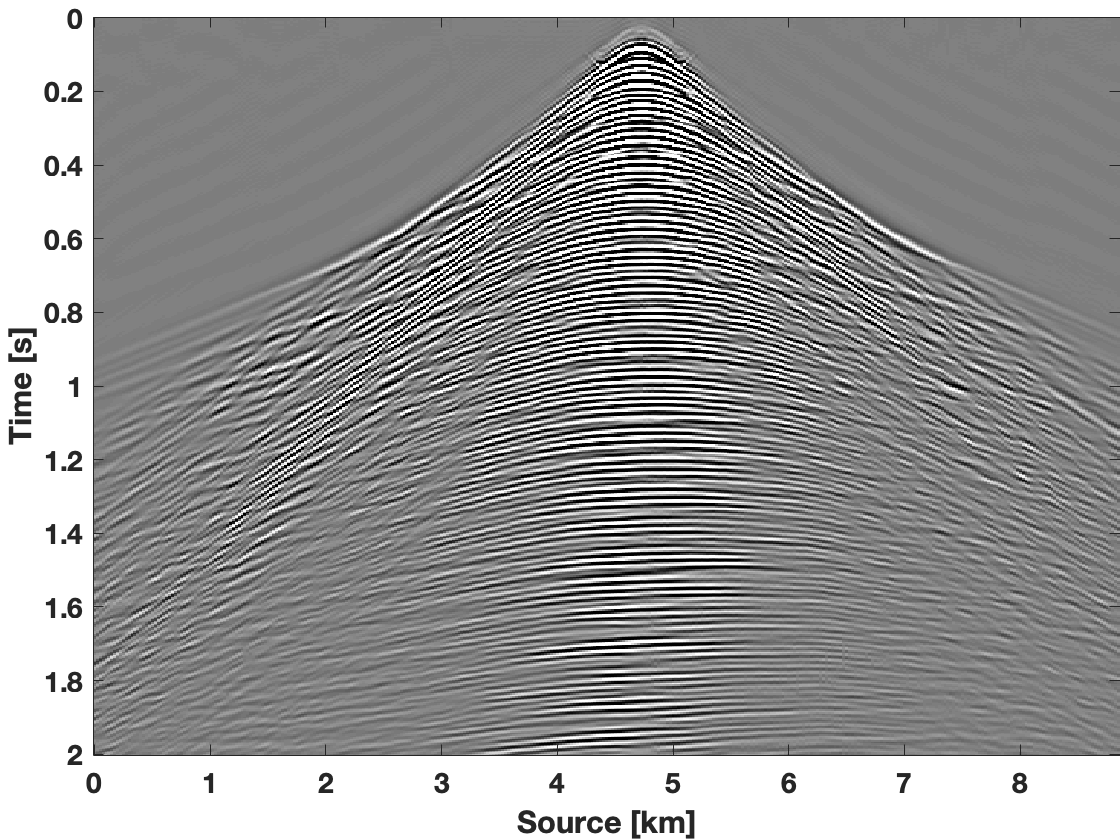
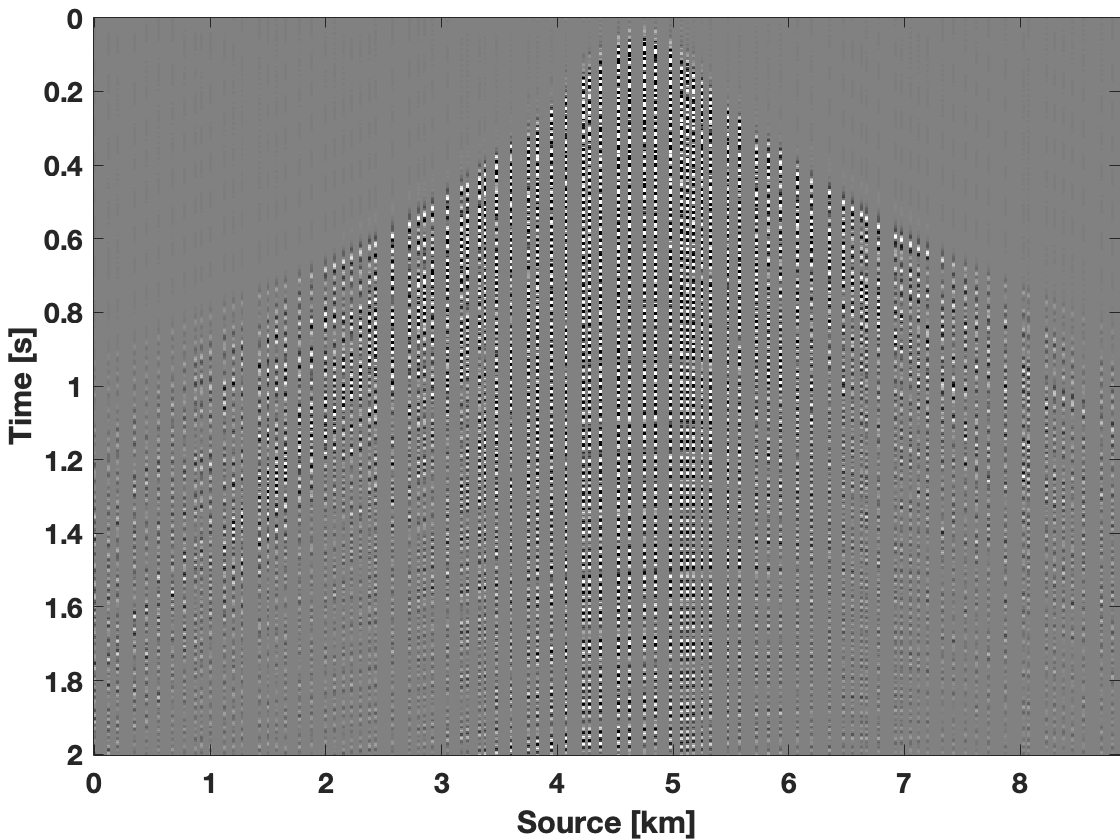
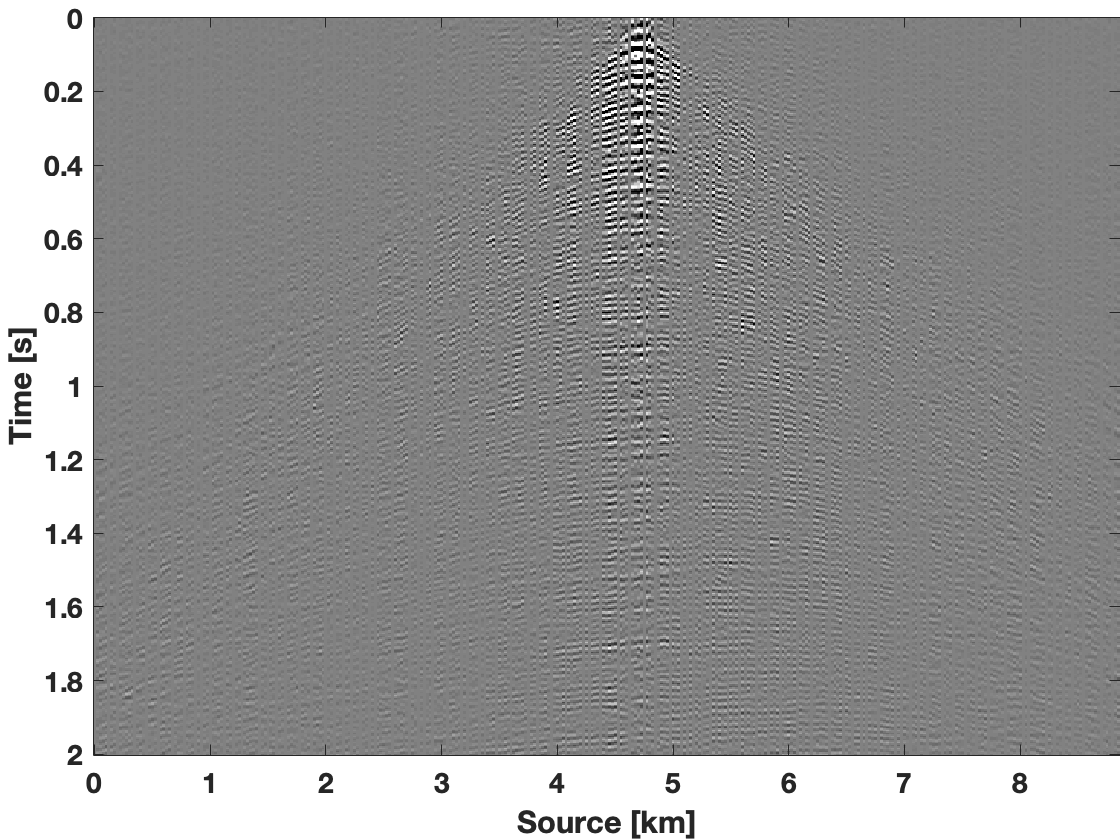
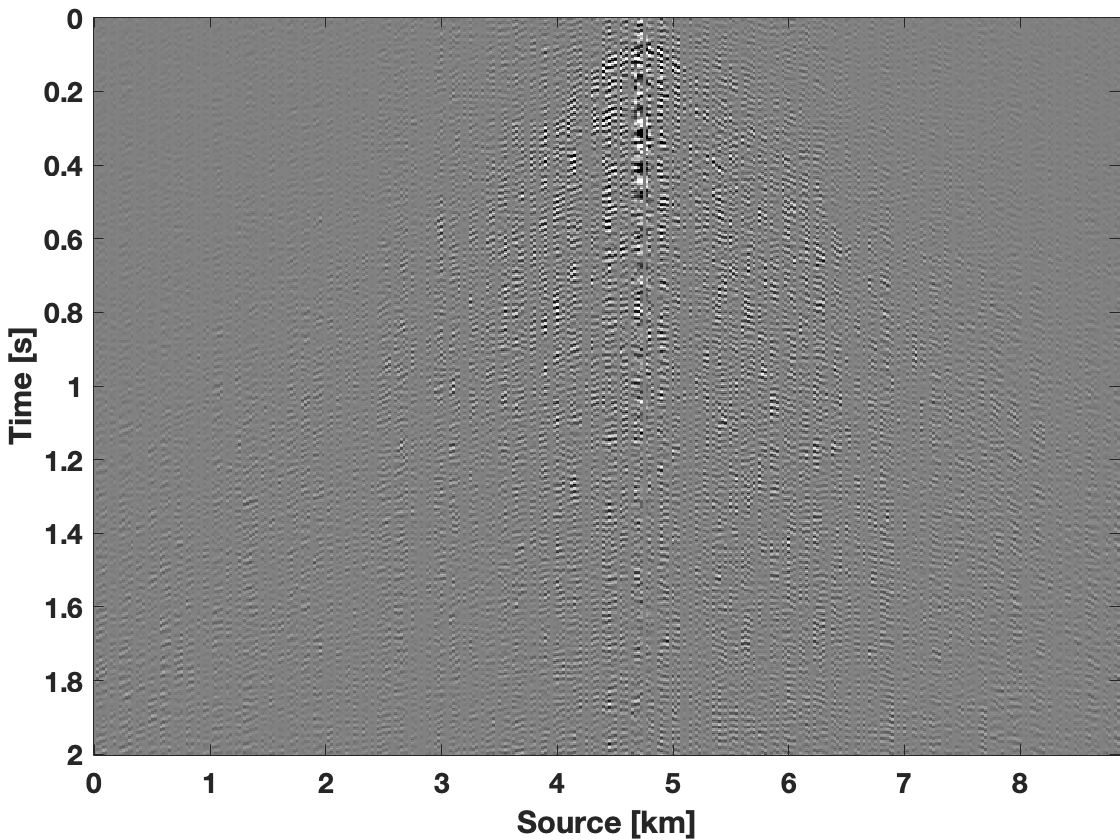
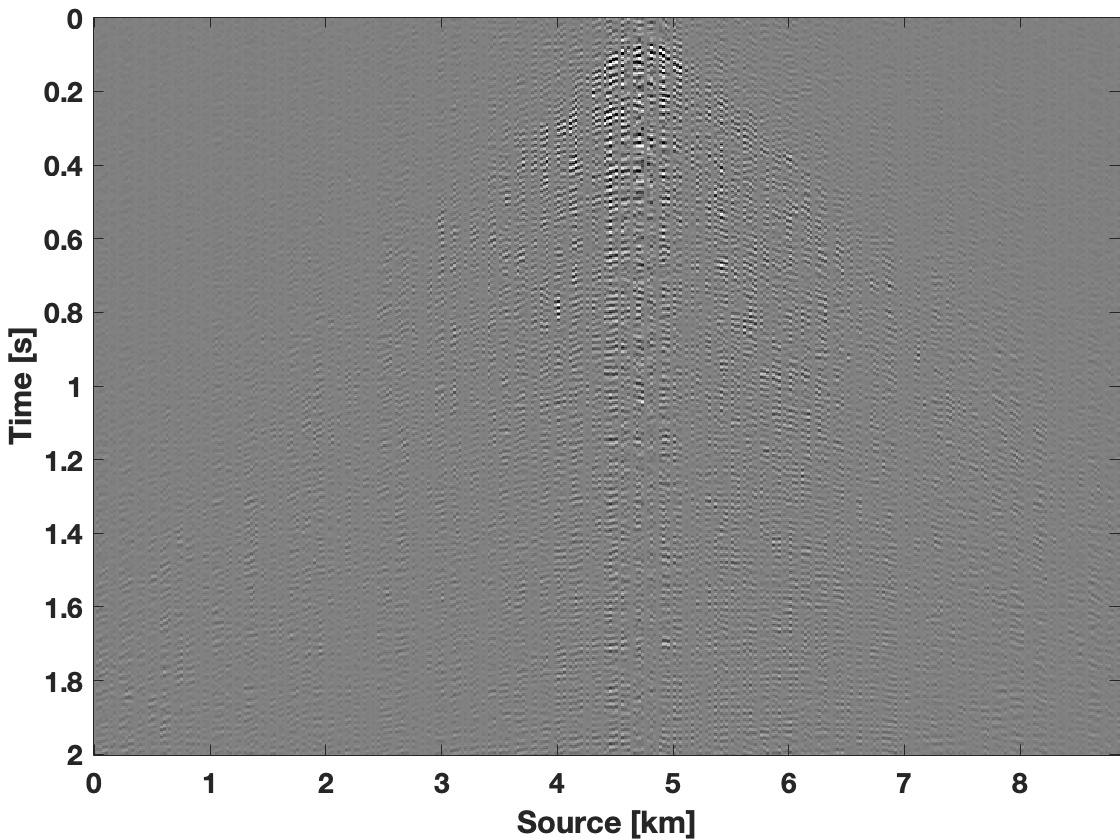
To show the recovery improvement in the time domain, we included Figure 3. To make fair comparison, we construct a bandpass filter with pass frequency \(7-74\, \mathrm{Hz}\) with a transition width at both ends of \(3.66\, \mathrm{Hz}\). We apply this bandpass filter on the true data, the subsampled data, and on recovered data recovered using the three scenarios described above. After applying the filter, we transform the filtered data back to the time domain. As we can see from Figure 3e, we observe less leakage of coherent signal in the data residual for results obtained with our limited-subspace weighted method in comparison to the data residual yielded by the conventional weighted method with ranks of \(r=85\) (Figure 3c) and \(r=25\) (Figure 3d). With the conventional weighted method for rank equals to \(r=85\), we get S/R of \(10.69\, \mathrm{dB}\), and for rank \(r=25\), we get S/R of \(11.49\, \mathrm{dB}\). With the limited-subspace weighted method we get S/R of \(13.31\, \mathrm{dB}\), which is a significant improvement.

Conclusions

In this work, we proposed a limited-subspace weighted method to further improve the performance of recursively weighted method in terms of better data reconstruction quality. By exploiting the fact that dimensions of weight matrices are independent of the rank of the subspaces, our method allows us to use higher ranks for data reconstruction while avoiding the risk of overfitting at the lower frequencies. Matrices with higher rank allow for a better approximation of the frequency slices at higher frequencies and hence allow for better quality of reconstructed data if we prevent overfitting by working with limited-subspace weights. Through experiments we performed on a field data acquired in the Gulf of Suez, we demonstrated the advantage of our method in comparison to the recursively weighted method without using limited subspace. We also introduced a computationally more efficient formulation by moving the weight matrices to the data-misfit term. In future work , we would like to extend the application of limited-subspace weighted method to large scale \(3\)D data examples.

Related materials

In order to facilitate the reproducibility of the results herein discussed, Matlab & Julia implementation of this work are made available on the SLIM GitHub page https://github.com/slimgroup/Software.SEG2020.

Acknowledgement

We would like to acknowledge the support from Georgia Institute of Technology for funding this research.