AVA classification as an unsupervised machine-learning problem

Ben B. Bougher and Felix J. Herrmann
Seismic Laboratory for Imaging and Modeling (SLIM), University of British Columbia

Introduction

In the most general sense, unsupervised learning is a subfield of machine learning that tries to infer hidden structure within an unlabeled dataset. Unsupervised methods are particularly useful when the inferred structure is lower dimensional than the original data. For example, given a list of \(n\) patients in a hospital and their corresponding symptoms \(s\), it is unlikely that each patient-symptom combination is unique. A set of common diseases \(d\) can be inferred from the data, where \(d \ll n,s\). Popular unsupervised learning and data mining methods such as principal component analysis (PCA) and K-Means clustering rely on exploiting low-dimensional structure inherent in the data (Ding and He, 2004).

Interestingly, interpreted images and geological maps produced by geoscience workflows are substantially lower dimension than the original field data. The structure of the major sedimentary layers of the Earth is relatively simple, as rocks with similar physical properties are formed along relatively continuous interfaces and facies in the subsurface. For this reason, we can use a combination of physical models, local geological knowledge, and experience to reduce large seismic and well-log datasets into low-dimensional models of the Earth. Abstractly, we are inferring a low-dimensional Earth model from high-dimensional geophysical data. In this respect, resevoir characterization can be posed as an unsupervised machine-learning problem.

In conventional AVA interpretation, two-term AVA attributes are extracted from seismic angle gathers using the Shuey approximation (Shuey, 1985) as a physical reflectivity model. Multivariate analysis of these attributes lead to an estimation of a background trend of shale-sand reflections and anomalous outliers that can be considered potential hydrocarbon indicators (J. P. Castagna et al., 1985; John P. Castagna et al., 1998). Although this has proven to be an effective workflow, the efficacy of the method requires calibrated seismic data processing that preserves reflection amplitudes throughout migration. In theory, amplitude preserving migration is feasible (Sava et al., 2001; Y. Zhang et al., 2014; Gajewski et al., 2002), however there are always large uncertainty and variations in measured AVA responses. Recent work by Hami-Eddine et al. (2012) applied neural networks to classify AVA anamolies, while Hagen (1982), Saleh et al. (2000), and Scheevel et al. (2001) used principal component analysis (PCA) to characterize pre-stack seismic data. We follow a similar philosophy and demonstrate that conventional AVA characterization can be reformulated as an unsupervised learning problem. In the vernacular of machine learning, the problem generalizes as dimensionality reduction followed by clustering.

Theory & Method

Starting with angle-domain common-image gathers, we desire a segmented output image where each pixel is classified according to the local AVA response. We define the angle gathers as feature vectors \(x_i \in \mathbb{R}^d,\, i \in [1,...n]\), where \(n\) is the number of samples in the image and \(d\) is the number of angles in the gather. The feature vectors are shaped into a matrix \(X \in \mathbb{R}^{n \times d}\), where each row corresponds to a point in the image and each column corresponds to an angle. Generalizing the data as a feature matrix allows us to work in an unsupervised learning framework (Figure 1).

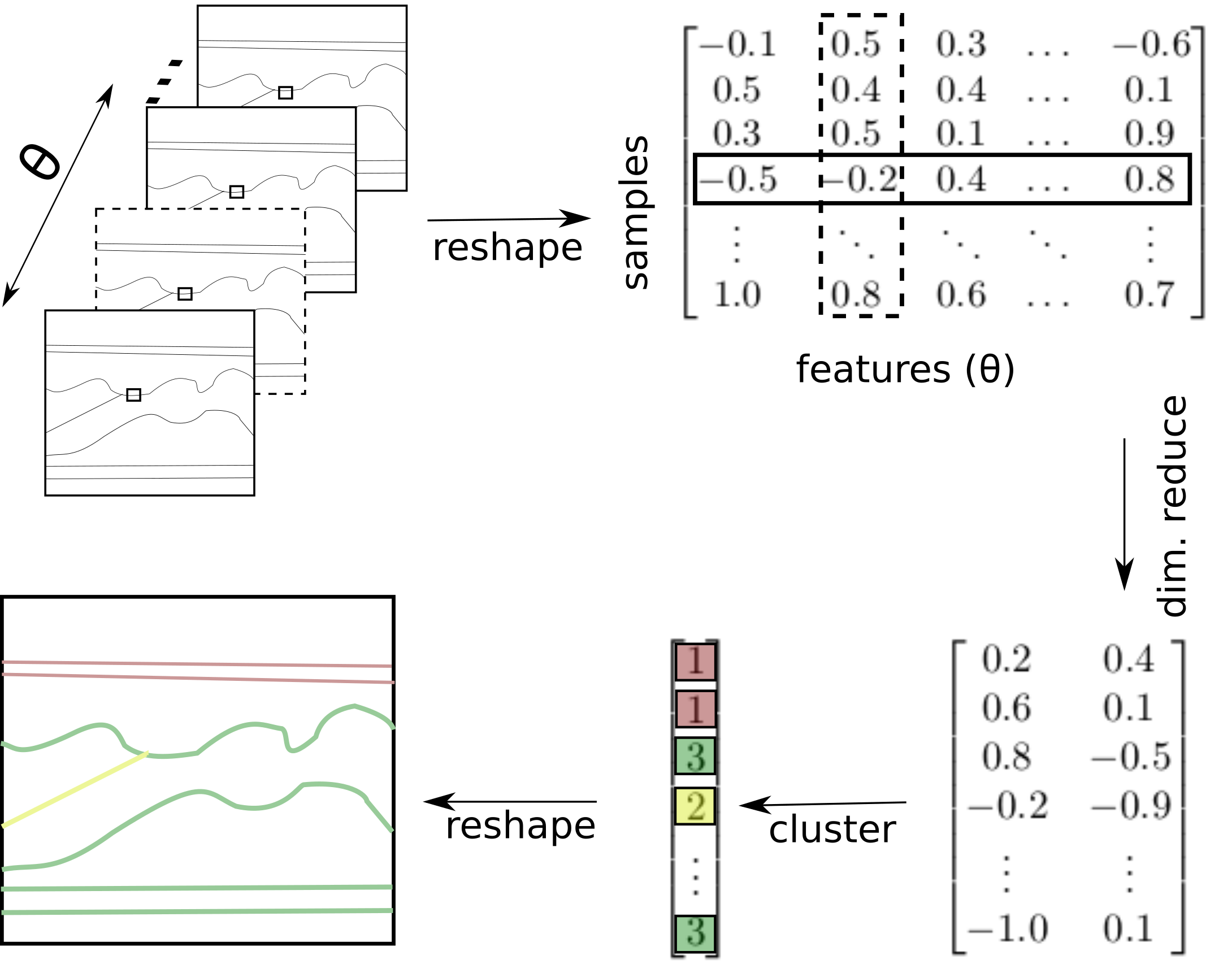
We assume that the columns of \(X\) are not independent, as the angle response of a reflection is often modeled by simple equations with as few as two parameters (e.g.. two-term Shuey equation). Assuming the existence of a lower-dimensional representation, we can use dimensionality reduction techniques to reduce the number of columns in \(X\) into a new feature matrix \(\hat{X} \in \mathbb{R}^{n\times m}, m<<d\).

PCA reduces dimensionality by keeping the \(m\) most significant eigenvectors from the decomposition of the covariance matrix \[ \begin{equation} \begin{aligned} G=X^T\!X=\begin{pmatrix} \langle x_1,x_1 \rangle & \langle x_1,x_2 \rangle & \dots & \langle x_1,x_n \rangle \\ \langle x_2,x_1 \rangle & \langle x_2,x_2 \rangle & \dots & \langle x_2,x_n \rangle \\ \vdots & \vdots & \ddots & \vdots \\ \langle x_n,x_1 \rangle & \langle x_n,x_2 \rangle & \dots & \langle x_n,x_n \rangle \\ \end{pmatrix}. \end{aligned} \label{eq:Gram} \end{equation} \] Although PCA will reduce the number of features while maximizing the variance of the data (a measure of information), it is a linear model which may not result in the best low-dimensional representation of \(X\). Note that the covariance matrix \(G\) depends only on the inner product of the feature vectors \(\langle x_i,x_j \rangle\) and not the features directly. We can thus replace the inner-products with a kernel function, which implicitly calculates a similarity measurement in a higher-dimensional feature space (Hofmann et al., 2008). Using a non-linear kernel function \(\kappa(x_i, x_j)\) will result in a non-linear PCA operation (Schölkopf et al., 1997). In this study, we found by trial that the polynomial kernel \[ \begin{equation} \kappa(x_i, x_j)=(x_i^Tx_j +c)^d \label{eq:kernel} \end{equation} \] with \(c=0\) and \(d=10\) provided the best clustering in our examples.

Assuming that common similarities in the rows of \(\hat{X}\) can be sorted into a finite set of groups, we can use a clustering algorithm to associate each sample to a group. Since there is no guarantee that the clusters will have Gaussian structure, methods that rely on Gaussian mixtures such as K-means are not appropriate for this application. Instead, we use BIRCH clustering (T. Zhang et al., 1996), which is a hierarchical clustering algorithm designed for large databases and makes no assumptions about underlying statistical distributions or cluster geometry. The output vector consists of the cluster identification number for each point, which is reshaped back into model dimensions resulting in a segmented image. Open-source software libraries Madagascar and scikit-learn were used for seismic processing and machine learning. All scripts are publically available at https://github.com/ben-bougher/thesis.

Example

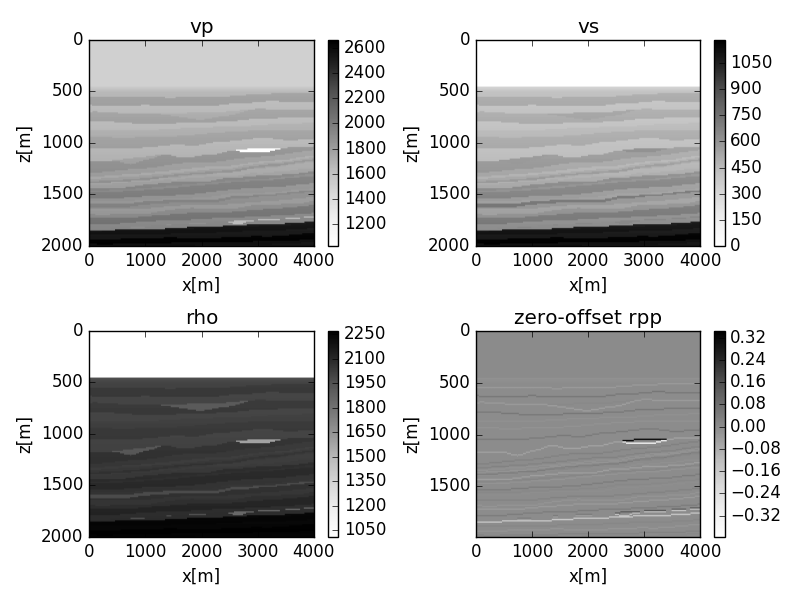
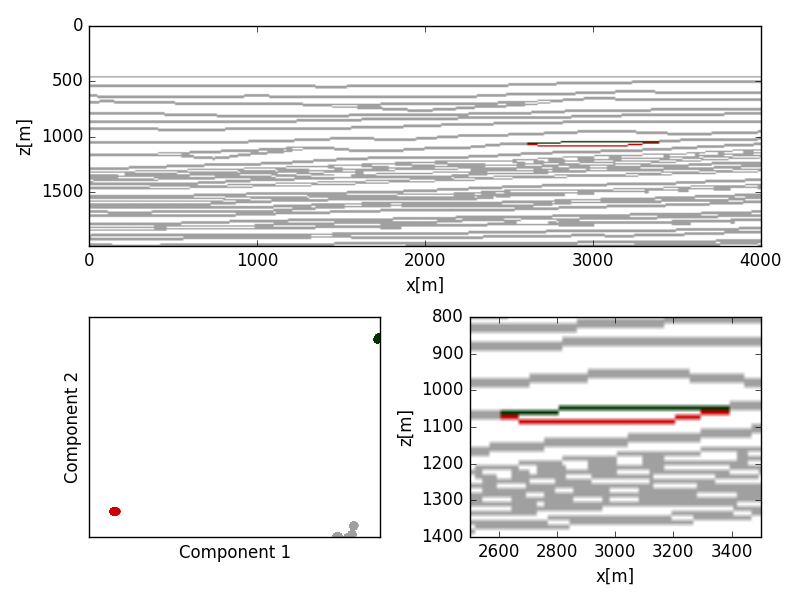
We tested the method using a subset of the elastic Marmousi II model (Martin et al., 2002) (Figure 2). This section of the model contains a gas reservoir embedded in layers of brine saturated sand and shales. We used the Zoeppritz equations to generate images of the true reflectivity response and also synthesized seismic gathers, which intentionally violate the amplitude preserving assumptions implied by conventional AVA analysis. The synthetic seismic was generated using visco-acoustic modeling and migrated using the sinking survey algorithm described by Sava and Fomel (2003), which does not preserve amplitude.

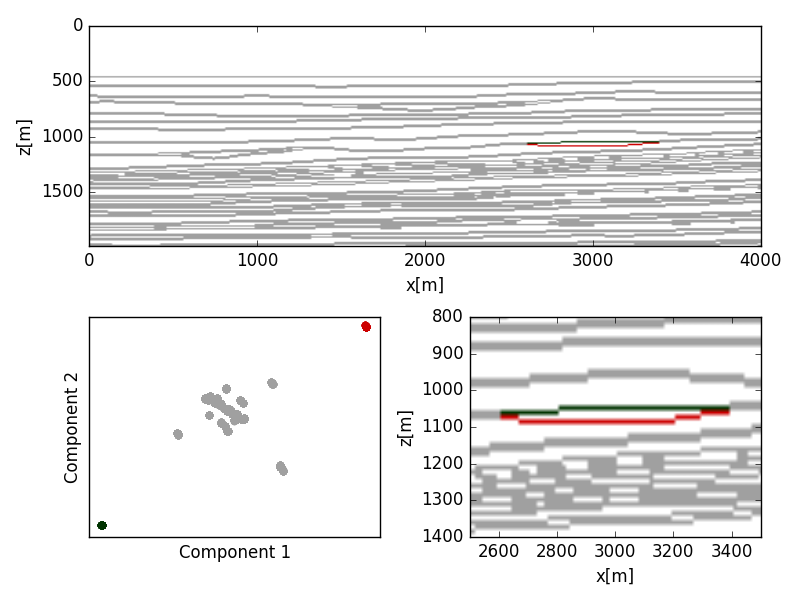
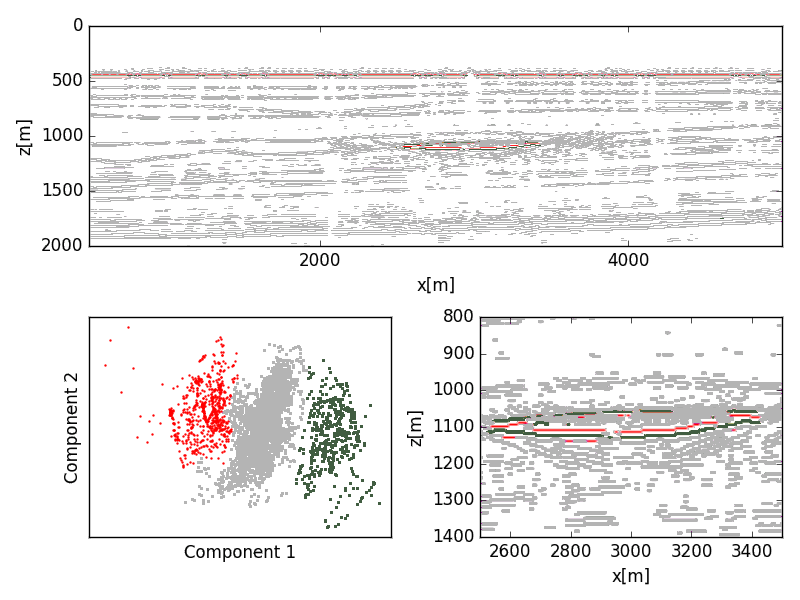
We ran the algorithm using PCA, kernelized PCA, and conventional two-term Shuey coefficients to reduce the datasets to two features. For the physically consistent data, all methods were able to cluster the background trend and anomalies, however the multivariate distribution of the reduced features showed interesting geometries. The Shuey terms (Figure 3) and linear PCA (Figure 4) showed remarkably similar reduced features, where the kernelized PCA (Figure 5) yielded tighter more distinct clusters.

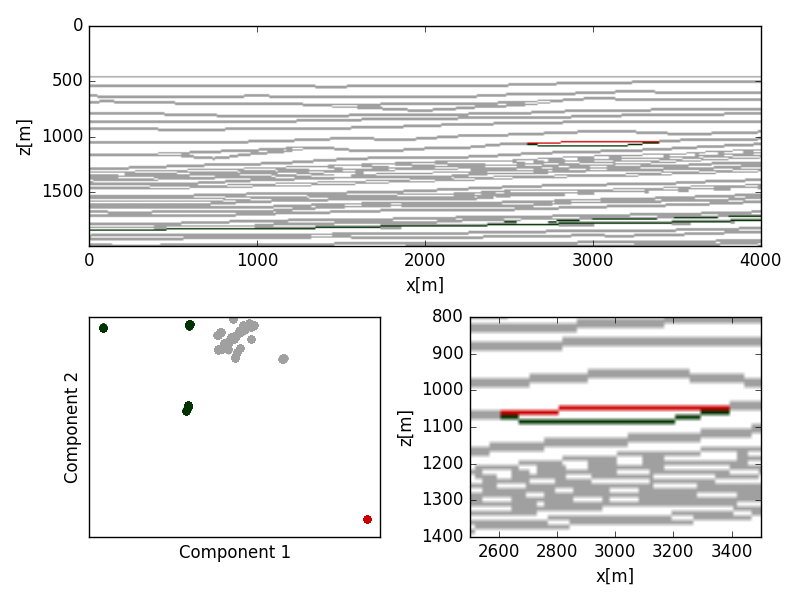
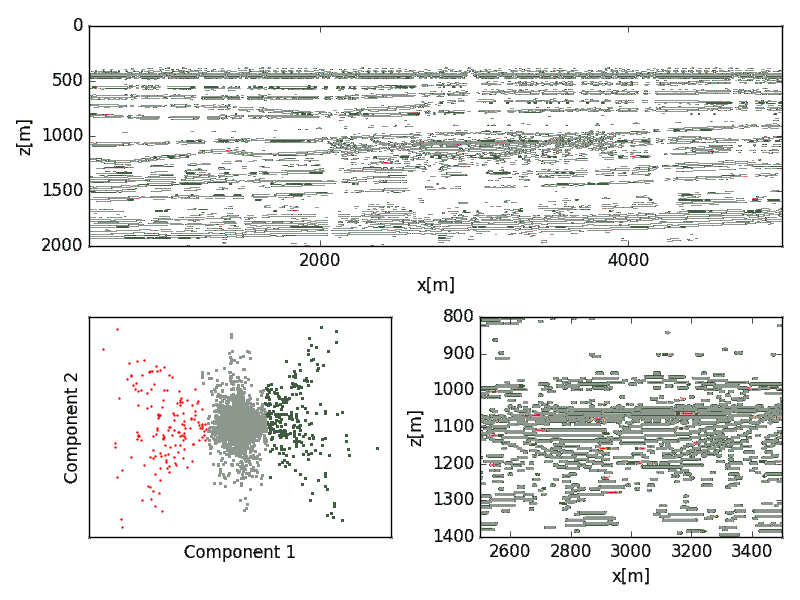
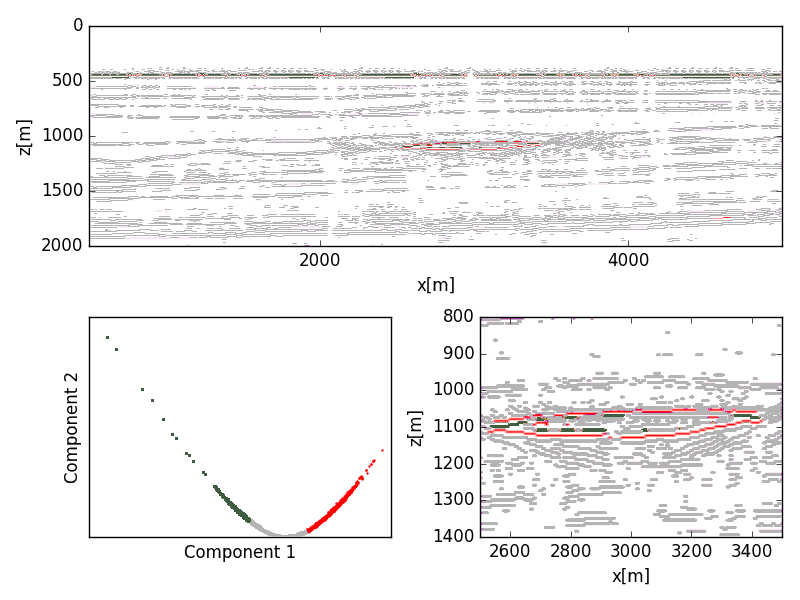
The migrated seismic was peak filtered and thresholded to filter for reflection events. Shuey terms were extracted from the migrated seismic data using a basic least-squares data fit. The poor correlation between the Shuey coefficients reflect the physical inconsistencies between the model and the migrated gathers. Clustering on the Shuey terms was not able to discriminate the reservoir from the background trend (Figure 6); however, both the PCA (Figure 7) and kernelized PCA (Figure 8) showed significant delineation of the reservoir.

Conclusions

AVA characterization was presented in an unsupervised machine learning framework. PCA and non-linear kernel PCA feature reduction algorithms were compared to conventional Shuey coefficients. Each approach was able to segment the true reflectivity image, however the conventional Shuey term approach failed to delineate gas reservoir in the migrated seismic image. The main result of this work is that AVA analysis can be reformulated as a machine learning problem, which can successfully characterize an image without physical or geological assumptions.

Acknowledgements

This work was financially supported in part by the Natural Sciences and Engineering Research Council of Canada Collaborative Research and Development Grant DNOISE II (CDRP J 375142-08). This research was carried out as part of the SINBAD II project with the support of the member organizations of the SINBAD Consortium.