Rank Minimization via Alternating Optimization\(:\) Seismic Data Interpolation.

Oscar Lopez^#
Rajiv Kumar^*
Felix J. Herrmann^*
#University of British Columbia, Department of Mathematics.
^*Seismic Laboratory for Imaging and Modeling (SLIM), University of British Columbia.

Introduction

Densely sampled seismic data is crucial for accurate inversion and imaging procedures such as Full Waveform Inversion, Reverse Time Migration and multiple removal methods (EPSI, SRME) where otherwise subsampled sources and receivers would result in unwanted image artifacts. To this end, various missing trace interpolation methodologies have been proposed that exploit some low dimensional structure of seismic data such as sparsity ((F. J. Herrmann and Hennenfent, 2007), (Mansour et al.)) and low-rank ((Yi et al., 2013), (Aravkin et al., 2014)), two key themes of compressive sensing literature. Thus, low-rank matrix completion techniques ((Candès and Plan, 2009), (E. Candès and Recht, 2009)) have recently become relevant in seismic trace interpolation problems. In work by (Aravkin et al., 2014), the authors utilize the low-rank structure of seismic data in midpoint-offset domain to allow for successful seismic data reconstruction. Furthermore, by allowing the data matrix to be factorized in bi-linear form as implemented by (Recht et al., 2010), these authors propose LR-BPDN a rank penalizing formulation that is suitable for large scale seismic interpolation problems.

While this approach yields state of the art results, it is subject to suboptimal performance when faced with increasingly complicated problems due to large scale, oscillatory data, or highly subsampled data. Since such cases encompass a large part of practical interest we see that we would greatly benefit from a more robust optimization procedure. The goal of this talk is to improve LR-BPDN in these aspects by proposing a modified optimization scheme, we consider a rank minimization work flow that alternates the optimization procedure between the bi-linear matrix factors. In this way we tackle one matrix factor at a time, which allows for a more tractable procedure that can overcome these impediments without increasing time complexity. Experiments on the Nelson 2D seismic line and Gulf of Mexico 7 Hz frequency slice demonstrate the potential of the new approach.

Matrix Completion\(:\) Large Scale Implementation

The goal of low-rank matrix completion is to accurately estimate the unobserved entries of a given incomplete data matrix from the observed entries and the prior knowledge that the matrix has few nonzero or quickly decaying singular values, i.e. the matrix exhibits low-rank structure. If we let \(\Omega\) be the set of observed entries, we can define our sampling operator \(P_{\Omega}\) by its action as \[ \begin{equation*} \begin{split} P_{\Omega}(X)=\left\{ \begin{array}{ll} X_{ij} \text{if} (i,j)\in\Omega\\ 0 \text{otherwise} \end{array} \right. \end{split} \end{equation*} \] where \(X\in \mathbb{C}^{n\times m}\). If \(X\) is our true matrix of interest, then our observations are given by \(b = P_{\Omega}(X) + n\), where \(n\) encompasses our corruption by noise. As introduced by (???) and shown by (Recht et al., 2010) we can approximately solve the rank minimization problem by instead minimizing the best convex approximation of the rank function, the nuclear norm. This convex relaxation gives us our data estimate \(X^{\sharp}\) as the argument output of the optimization procedure \[ \begin{equation} \label{eq:NN} \min_{Y\in \mathbb{C}^{n\times m}} ||Y||_* \text{s.t.} ||P_{\Omega}(Y)-b||_F \leq \epsilon \end{equation} \] where \(||n||_F \leq \epsilon\) is the noise level in our observations, \(||Y||_*\) is the nuclear norm of the matrix \(Y\) and \(||X||_F\) denotes the Frobenius norm of the matrix \(X\). This procedure exploits the knowledge that \(X\) has low-rank structure while making sure we agree with our observations up to some known noise level.

Many implementations to solve (\(\ref{eq:NN}\)), such as singular value projection and singular value tresholding ((Meka et al., 2009), (Cai et al., 2010)) require numerically expensive SVD computations of our data matrix at each iteration and furthermore require full matrix storage. Since these issues can make (\(\ref{eq:NN}\)) impractical for large data matrices, (Recht et al., 2010) and (Aravkin et al., 2014) propose a matrix factorization approach to overcome this impediment. By choosing \(r\ll \min(n,m)\), the authors write the matrix in bi-linear form \(X = LR^{H}\), where \(L\in \mathbb{C}^{n\times r}\), \(R\in \mathbb{C}^{m\times r}\) and \(R^{H}\) denotes the Hermitian transpose of \(R\). As shown by (Srebro, 2004) and (Recht et al., 2010), the fact that \(||X||_* = \min_{\{L,R: X = LR^H\}}\frac{1}{2}(||L||_F^2 + ||R||_F^2)\) allows us to solve (\(\ref{eq:NN}\)) by instead solving \[ \begin{equation} \label{eq:LR} \min_{L\in \mathbb{C}^{n\times r}, R\in \mathbb{C}^{m\times r}} \frac{1}{2}(||L||_F^2 + ||R||_F^2) \text{s.t.} ||P_{\Omega}(LR^H)-b||_F \leq \epsilon. \end{equation} \] If we choose our factorization parameter, \(r\), significanly smaller than the ambient dimensions \(n\) and \(m\), we have reduced our memory requirements from \(mn\) to \(rn + rm\) while implementing a rank penalization scheme that avoids computing SVD of our potentially large data matrix.

In this talk we adopt formulation (\(\ref{eq:LR}\)) and consider the following algorithm for this purpose

  1. \(\text{input:}\) \(P_{\Omega}\), \(b\), \(r\), \(T\)
  2. \(\text{initialize:}\) \(L^0\) \(r\)  \(b\) 
    3. for \(t = 0 \) to \(T-1\) 
  4. \(R^{t+1} \leftarrow \min_{\{R\in \mathbb{C}^{m\times r}\}} \frac{1}{2}||R||_F^2\) s.t. \(||P_{\Omega}(L^tR^H)-b||_F \leq \epsilon\)
  5. \(L^{t+1} \leftarrow \min_{\{L\in \mathbb{C}^{n\times r}\}} \frac{1}{2}||L||_F^2\) s.t. \(||P_{\Omega}(L(R^{t+1})^H)-b||_F \leq \epsilon\)
  6. end for
  7. output: \(X^{\sharp} = L^T(R^T)^H\)

The key component of Algorithm 1, is to allow our optimization to focus on a single matrix factor at a time in steps 2 - 5. As we will see in the experiments section, this choice of implementation results in a favorable output for cases where our data matrix is large, highly oscillatory or critically subsampled.

Similar alternating techniques have been proposed and discussed by (Jain et al., 2013) and (Xu and Yin, 2013). However the approach considered by (Jain et al., 2013) does not penalize the rank and while Algorithm 1 is a consequence of the work in (Xu and Yin, 2013), the authors do not provide a specific implementation to achieve steps 3 and 4. For this purpose we utilize a generalization of the SPG\(\ell_1\) solver (Berg and Friedlander, 2009) which at step \(t\) given \(L^t\) solves step 3 of Algorithm 1 by solving a sequence of LASSO subproblems \[ \begin{equation*} \min_{\{R\in \mathbb{C}^{m\times r}\}} ||P_{\Omega}(L^tR^H)-b||_F \text{s.t.} \frac{1}{2}||R||_F^2 \leq \tau \end{equation*} \] Where \(\tau\) is a regularization parameter updated appropriately by SPG\(\ell_1\) so that the LASSO optimization procedure is equivalent to solving step 3. Solving such LASSO subproblems requires us to minimize a convex funtion (\(||P_{\Omega}(L^tR^H)-b||_F\) as a function of \(R\) only) and project onto \(\frac{1}{2}||R||_F^2 \leq \tau\), which is easily achieved by appropriate scalar multiplication. We thus end up with a sequence of tractable convex problems that do not require expensive SVD computations and effectively penalize the rank. Solving step 4 of Algorithm 1 can be done in a similar manner.

Seismic Data Reconstruction via Rank Minimization\(:\) Experiments

We allow our monochromatic frequency slice, \(X\in \mathbb{C}^{n\times m}\), to be organized as a matrix in midpoint-offset (m-h) domain. As (Aravkin et al., 2014) discuss, implementing (\(\ref{eq:LR}\)) in m-h domain allows us to achieve low-rank structure and furthermore results in successful low-rank matrix completion since in m-h domain missing sources and receivers result in missing matrix entries whose structure disrupts the low-rank properties of our complete matrix. Furthermore we simulate the effect of missing traces by applying a subsampling mask that removes a desired percentage of sources in a jittered random manner. As mentioned by (Kumar et al., 2014) jittered subsampling allows for randomness in our sampling scheme, a key component in compressive sensing applications, while controlling the allowed gap sizes of our missing data, an important consideration for interpolation techniques.

We offer two experiments to demostrate our interpolation scheme, where for the sake of comparison we also implement LR-BPDN proposed by (Aravkin et al., 2014). The first is conducted on a single 7 Hz frequency slice extracted from the Gulf of Mexico dataset with 4001 sources and 4001 receivers. We apply a sampling mask that removes 90\(\%\) of sources in a jittered random manner. For Algorithm 1 we choose a total of \(T = 10\) alternations with 15 iterations of SPG\(\ell_1\) per alternation. For fairness of comparison we run LR-BPDN with 300 iterations of SPG\(\ell_1\) and choose factorization parameter \(r = 80\) for both methods. The results figure 1 demonstrate a drastic benefit offered by our approach. Results of LR-BPDN introduce more noise than signal in the reconstruction with and SNR of -.9 dB, whereas the results of Algorithm 1 give output with SNR of 6.7 dB. This critical difference in results shows how our proposed method does indeed improve results in large scale and highly subsampled cases.

The second experiment is conducted on a seismic line from the Nelson dataset with 401 sources, 401 receivers and 1024 time samples where we interpolate in the 1-97 Hz frequency band. For this experiment we subsample by removing 80\(\%\) of sources in a jittered random manner. In this case we choose \(T = 6\) alternations with 15 iterations of SPG\(\ell_1\) per alternation for Algorithm 1, 180 iterations of SPG\(\ell_1\) for LR-BPDN and choose the same factorization parameters adjusted from low to high frequency. We observe in figure 2 that implementation of Algorithm 1 offers an average improvement in SNR by a factor of .5 dB when compared to LR-BPDN. We further notice that reconstruction improvements are most apparent in the higher frequency slices (50-70 Hz), which enforces our previous statement that Algorithm 1 is most beneficial in cases where our data is highly oscillatory and critically subsampled. We remind the reader that while this might not seem like a critical improvement, we are not increasing the time complexity of LR-BPDN.

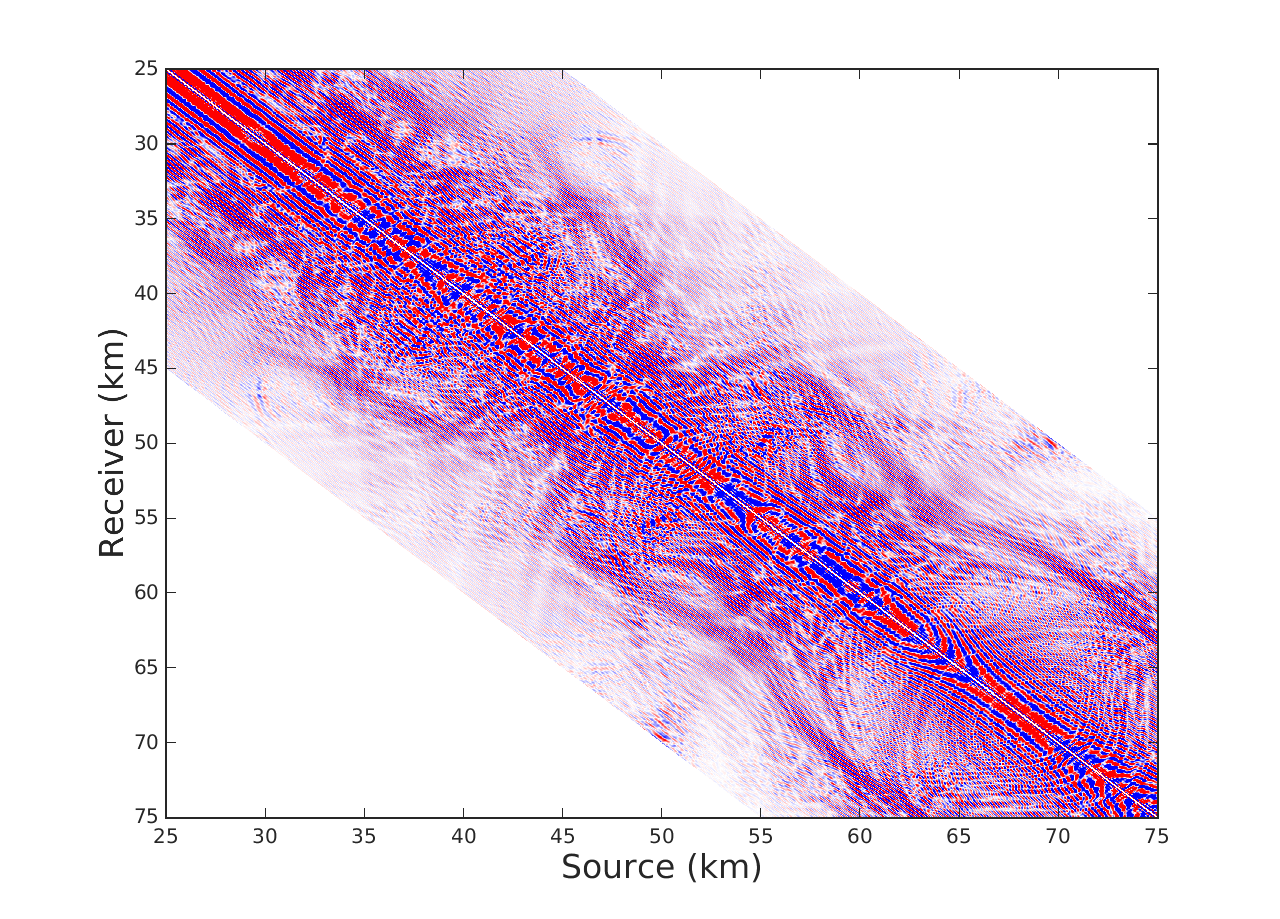
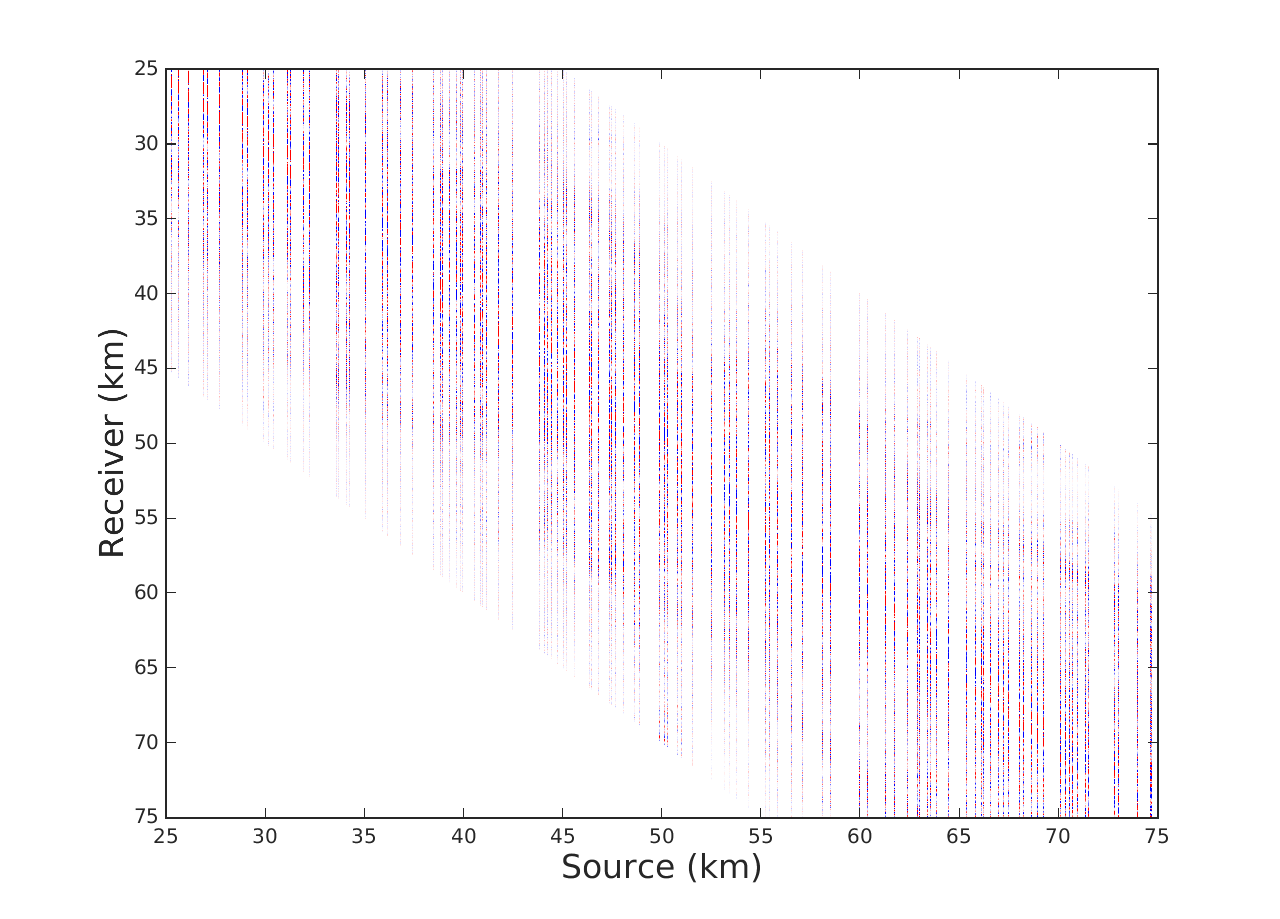
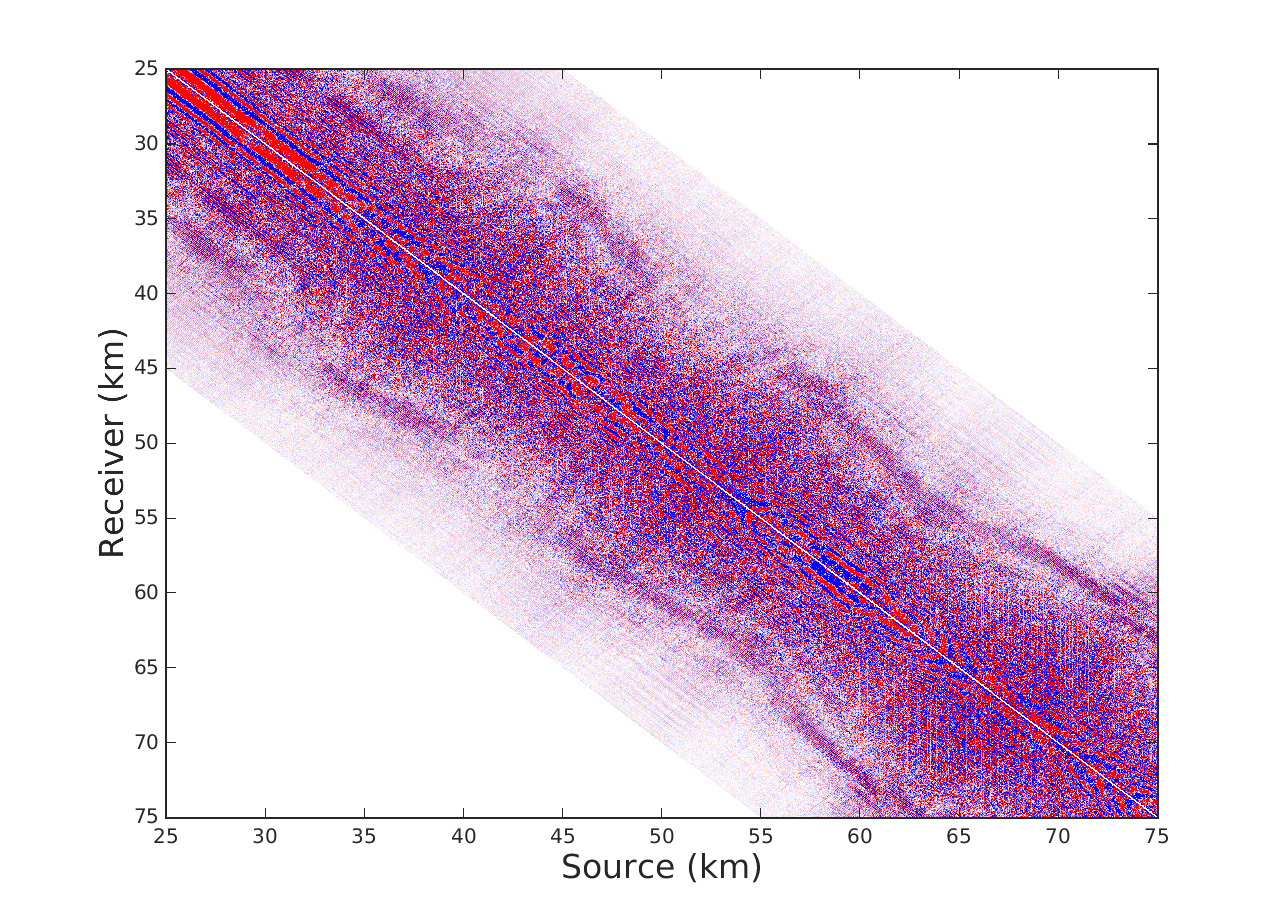
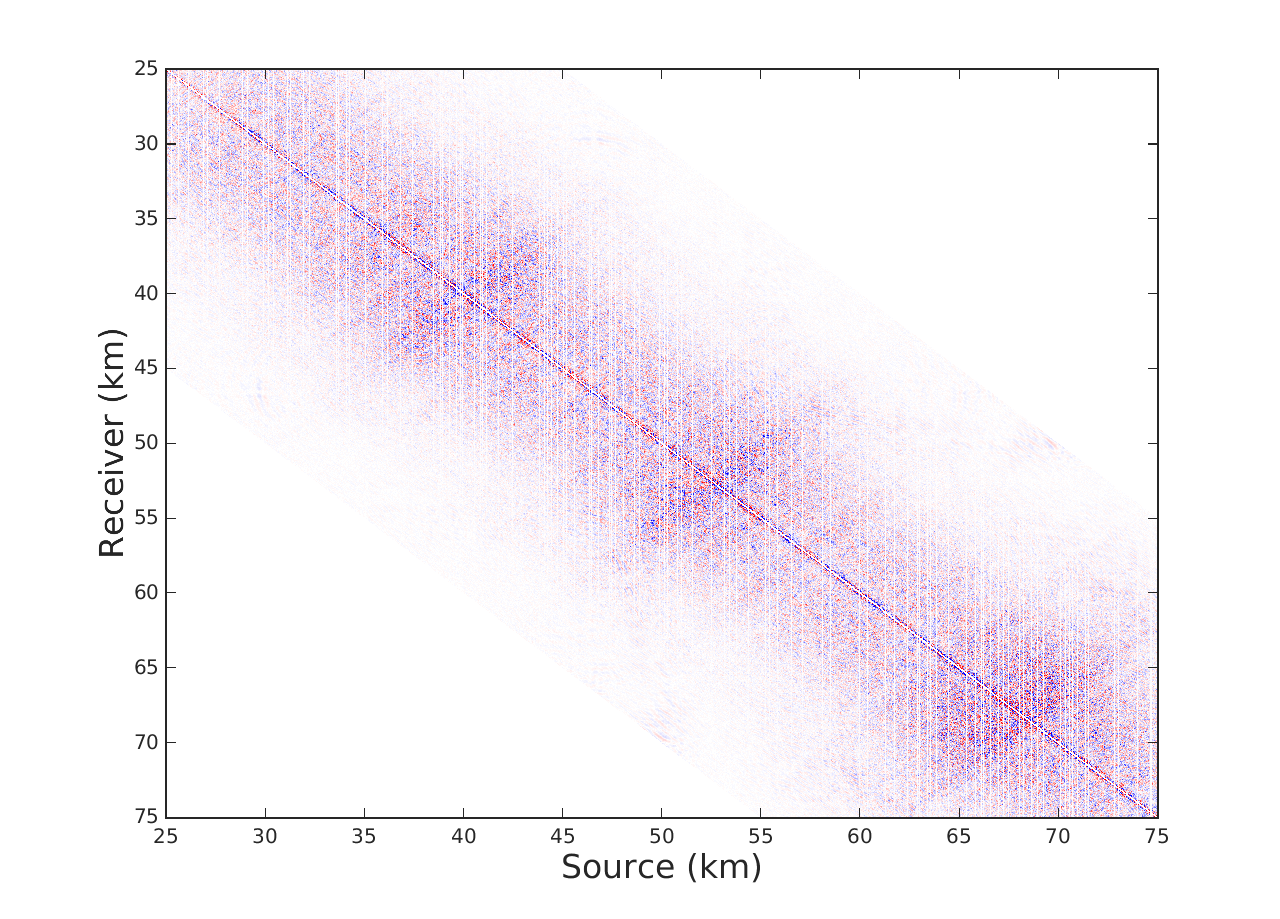
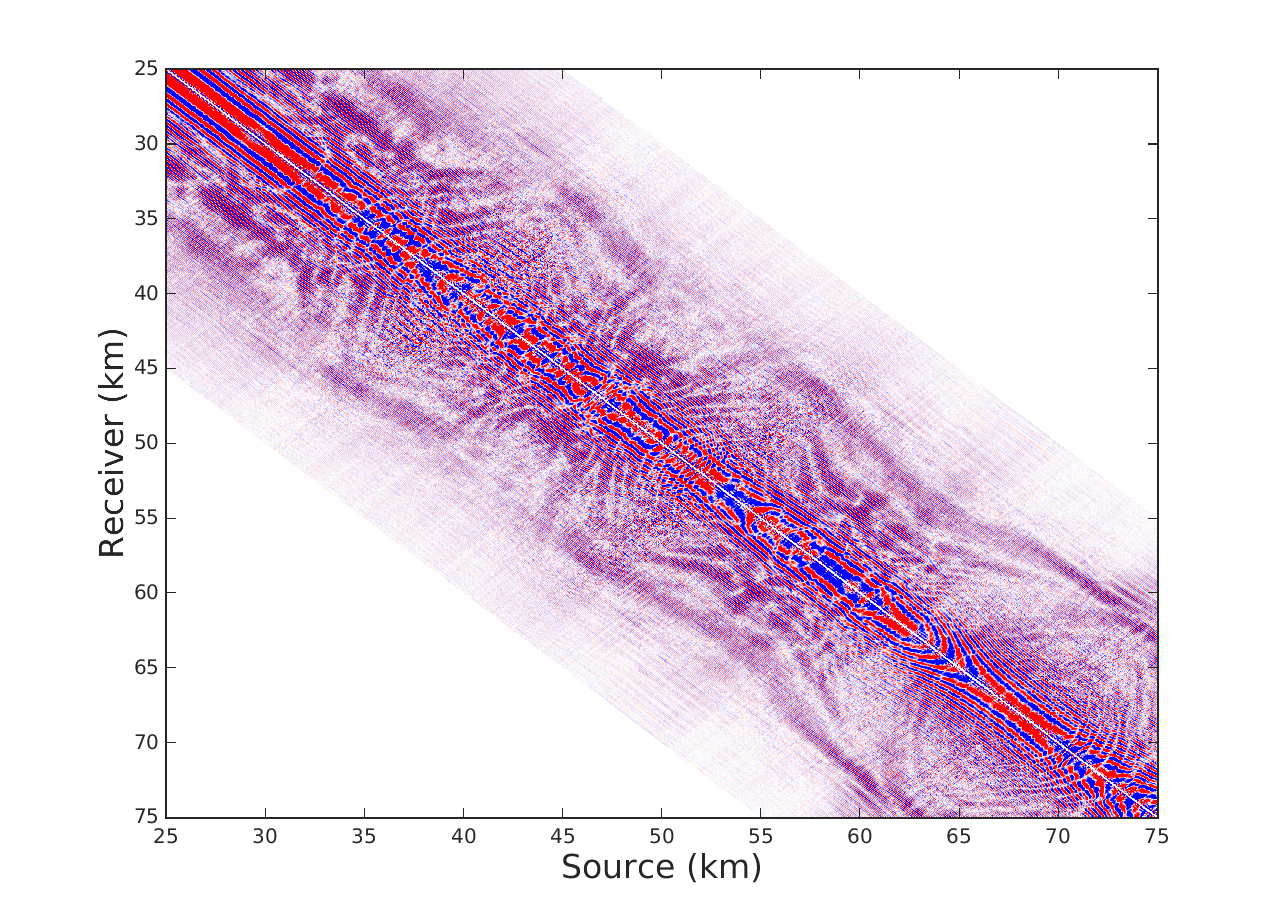
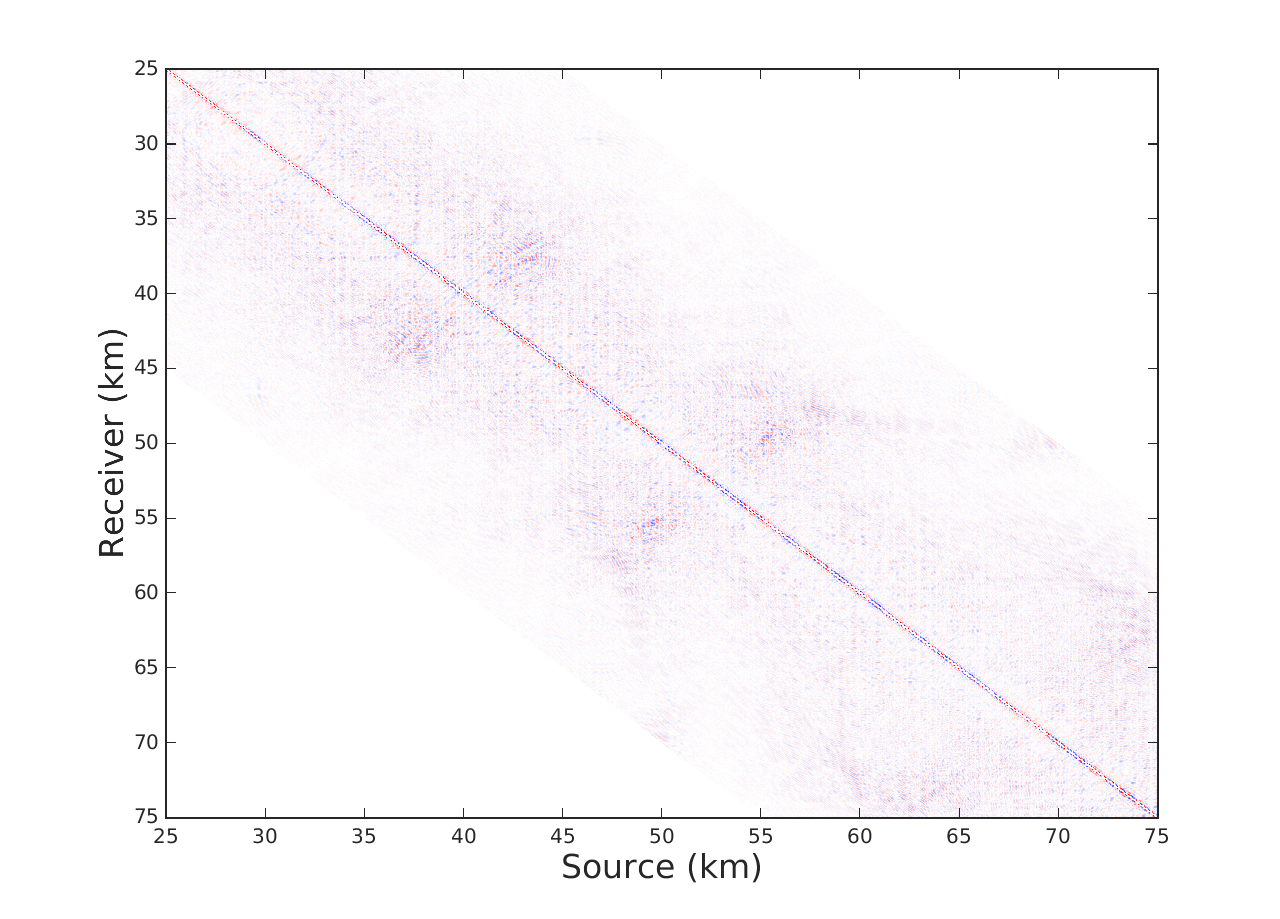
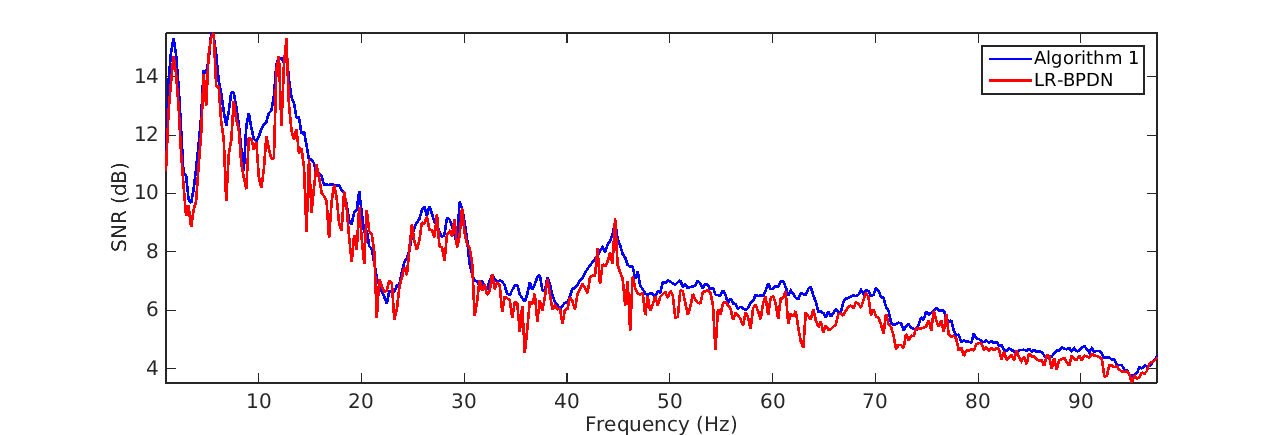
Conclusions

We proposed a modified optimization workflow for seismic data interpolation via low-rank matrix completion. In order to implement the nuclear norm minimization problem (\(\ref{eq:NN}\)), we proceed as (Aravkin et al., 2014 )but offer a different rank minimization approach. By allowing our optimization scheme to alternate between matrix factors and implementing the Pareto curve approach (SPG\(\ell_1\)) we are left with a sequence of tractable convex problems that do not require expensive SVD computations and effectively penalize the rank. This results in a more robust procedure, where the experimental results clearly highlight the reconstruction SNR improvements in cases where our data matrix is large, highly oscillatory and critically subsampled when compared to the LR-BPDN implementation.

Acknowledgements

This work was in part financially supported by the Natural Sciences and Engineering Research Council of Canada Discovery Grant (22R81254) and the Collaborative Research and Development Grant DNOISE II (375142-08). This research was carried out as part of the SINBAD II project with support from the following organizations\(:\) BG Group, BGP, CGG, Chevron, ConocoPhillips, ION, Petrobras, PGS, Statoil, Total SA, Sub Salt Solutions, WesternGeco, and Woodside.