3D time-domain acoustic isotropic modelling and linearized modelling demo

The modeling operator is based on a star 1D stencil of order 2,4 or 6. It solves the system in parallel over sources . Source injection and receiver sampling is done via cubic interpolation and exponential damping over a 3x3 square around the source location. The Jacobian is derived by linearizing the discretized system and its forward and adjoint action is calculated via the adjoint-state method.

The basic syntax of the modeling operator is data = Gen_data(m,Q,model,density,anisotropy)|, where

• m is a vector with a gridded slowness-squared model [km^2/s^2],
• Q is a vectorof that defines the source,
• model is a struct with various other parameters,
• data is a vectorized data-cube (receiver x source x time),
• density is the density
• anisotropy are the thompsen parameters

ANISOTROPY IS NOT YET SUPPORTED IN 3D, ONLY ISOTROPIC.

We illustrate the basic modeling capabilities on a simple layered model.

Contents

medium parameterss

o = [0 0 0]; % Origin
n = [50 50 50]; % Dimension
N = prod(n);
d = [15 15 15]; % Grid size
v = ones(n)*1.400; % velocity [m/s]
v(20:35,:,:) = 2.000;
v(36:end,:,:) = 3.000;
v = v(:);

m=1./v.^2;

Model containing acquisition geometry and modelling parameters

model.o=o; %Origins of the axes [m]
model.n=n; %Number of grid points  for each dimension (excluding boundaries)
model.d=d;
model.ddcompx=2; % Domain decomposition x direction
model.ddcompy=1; % Domain decomposition y direction
model.ddcompz=1; % Domain decomposition z direction
model.f0=0.010; % in [kHz]
model.xsrc =375;
model.zsrc= 10*ones(size(model.xsrc)); %Source coordinates along z axis [m]
model.ysrc=375*ones(size(model.xsrc));
model.xrec = 0:15:750;
model.zrec=10; %Receivers coordinates along z axis [m]
model.yrec=0:30:750; %Receivers coordinates along y axis [m]
model.T=1000; %Acquisition duration [ms]
model.freesurface=0; % Freesurface ( 0 : no freesurface, 1 : freesurface)
model.space_order=2; % Space discretization order (2 or 4 only for now)
model.type='full';
model.gppwl = 5;    % grid points per wave length (only for anisotropy)

parpool(model.ddcompx*model.ddcompy*model.ddcompz); % Open parrallel pool for multiple domains
%parpool(model.ddcompx*model.ddcompy*model.ddcompz+1); % Open parrallel pool for multiple domains in non-interactive session (one master + N domains)

Starting parallel pool (parpool) using the 'local' profile ... connected to 2 workers.

Acoustic isotropic modeling

[m1,model1]=Setup_CFL(m,model);
model1.NyqT=0:4:model1.T;
q=sp_RickerWavelet(model1.f0,1/model1.f0,model1.dt,model1.T);

tic;
dataT1=Gen_data(m1,model1,q);
toc

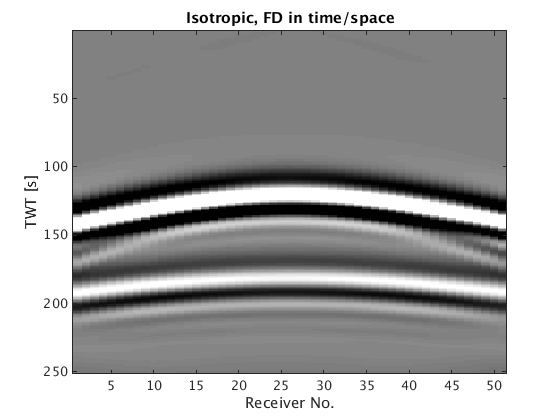
CFL conditions gives dt = 2.4249ms and d = 14  14  14 m 
Velocity interpolated on new grid
Lab 1: 
  shot = 375
  Acoustic isotropic
Elapsed time is 32.938270 seconds.

Reshape and display results

dataT1=reshape(dataT1,length(model1.NyqT),length(model1.xrec),length(model1.yrec),length(model1.xsrc));
rec = 1:length(model1.xrec); tt = 1:model1.T/1000;
figure(3); imagesc(rec,tt,dataT1(:,:,floor(length(model1.yrec)/2))); caxis([-1 1]);colormap(gray);
title('Isotropic, FD in time/space'); xlabel('Receiver No.'); ylabel('TWT [s]')

Born modelling

The basic syntax of the Born modeling operator is du = Born(m,Q,model,din,mode,density,anisotropy)|, A more detailed documentation of the function will be added in a Time imaging section where

Smooth model

S  = opKron(opSmooth(n(3),20),opSmooth(n(2),20),opSmooth(n(1),20));  %smoothing operator
v0=S*v(:);
m0=1./v0.^2;
% Model perturbations
dm=m-m0;

Linearized acoustic isotropic

You need to put dm in the Setup_CFL to project it on the new grid as well

[m1,model1,dm1]=Setup_CFL(m0,model,dm);
model1.NyqT=0:4:model1.T;
q=sp_RickerWavelet(model1.f0,1/model1.f0,model1.dt,model1.T);
du1=Born(m1,model1,q,dm1,1);

delete(gcp);

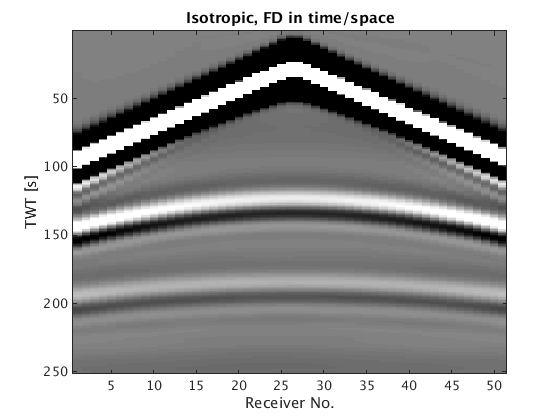
CFL conditions gives dt = 2.4249ms and d = 14  14  14 m 
Velocity interpolated on new grid
Lab 1: 
  J for shot  1 over 1 at position 375
  Acoustic isotropic
Parallel pool using the 'local' profile is shutting down.

Reshape and display results

du1=reshape(du1,length(model1.NyqT),length(model1.xrec),length(model1.yrec),length(model1.xsrc));
rec = 1:length(model1.xrec); tt = 1:model1.T/1000;
figure(4); imagesc(rec,tt,du1(:,:,floor(length(model1.yrec)/2))); caxis([-5 5]*1e-1);colormap(gray);
title('Isotropic, FD in time/space'); xlabel('Receiver No.'); ylabel('TWT [s]')