WISE: full-Waveform variational Inference via Subsurface Extensions

Introduction

Full-waveform inversion (FWI) plays a pivotal role in exploration, primarily focusing on estimating Earth’s subsurface properties from observed seismic data. The inherent complexity of FWI stems from its nonlinearity, further complicated by ill-posedness and computational intensiveness of the wave modeling. To address these challenges, we introduce a computationally cost-effective probabilistic framework that generates multiple migration-velocity models conditioned on observed seismic data. By combining deep learning with physics, our approach harnesses advancements in variational inference (VI, Jordan et al., 1999) and generative artificial intelligence (AI, Diederik P Kingma and Welling, 2013; Goodfellow et al., 2014; D. J. Rezende et al., 2014). We achieve this by forming common-image gathers (CIGs), followed by training conditional normalizing flows (CNFs) that quantify uncertainties in migration-velocity models.

Our paper is organized as follows. First, we delineate the FWI problem and its inherent challenges. Subsequently, we explore VI to quantify FWI’s uncertainty. To reduce VI’s computational costs, we introduce physics-informed summary statistics and justify the use of CIGs as these statistics. Our framework’s capabilities are validated through two case studies, which include studying the effects of uncertainty in the generated migration-velocity models on migration.

Methodology

We present a Bayesian inference approach to FWI by briefly introducing FWI and VI used as a framework for uncertainty quantification (UQ).

Full-waveform inversion

Estimation of unknown migration-velocity models, \(\mathbf{x}\), from noisy seismic data, \(\mathbf{y}\) involves inverting nonlinear forward operator, \(\mathcal{F}\), which links \(\mathbf{x}\) to \(\mathbf{y}\) via \(\mathbf{y} = \mathcal{F}(\mathbf{x}) + \boldsymbol{\epsilon}\) with \(\boldsymbol{\epsilon}\) measurement noise. Source/receiver signatures are assumed known and absorbed into \(\mathcal{F}\). Solving this nonlinear inverse problem is challenging because of the noise, the non-convexity of the objective function, and the non-trivial null-space of the modeling (Tarantola, 1984). As a result, multiple migration-velocity models fit the data, necessitating a Bayesian framework for UQ.

Full-waveform inference

Rather than seeking a single migration-velocity model, our goal is to invert for a range of models compatible with the data, termed “full-waveform inference”. From a Bayesian perspective, this involves determining the posterior distribution of migration-velocity models given the data, \(p(\mathbf{x}|\mathbf{y})\). We focus on amortized VI, which exchanges the computational cost of posterior sampling for neural network training (Rizzuti et al., 2020; Ren et al., 2021; Siahkoohi and Herrmann, 2021; X. Zhang et al., 2021, 2023; Gahlot et al., 2023). Specifically, we employ amortized VI, which incurs offline computational training cost but enables cheap online posterior inference on many datasets \(\mathbf{y}\) (Kruse et al., 2021). Next, we discuss how to use CNFs for amortized VI.

Amortized variational inference with conditional normalizing flows

During VI, the posterior distribution \(p(\mathbf{x}|\mathbf{y})\) is approximated by the surrogate, \(p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{y})\), with learnable parameters, \(\boldsymbol{\theta}\). Given the sample pairs \(\{(\mathbf{x}^{(i)}, \mathbf{y}^{(i)})\}_{i=1}^N\), CNFs are suitable to act as surrogates for the posterior because of their low-cost training and rapid sampling (D. Rezende and Mohamed, 2015; Louboutin et al., 2023). Their training involves minimization of the Kullback-Leibler divergence between the true and surrogate posterior distribution. In practice, this requires access to \(N\) training pairs of migration-velocity model and observed data to minimize the following objective: \[ \begin{equation} \underset{\boldsymbol{\theta}}{\operatorname{minimize}} \quad \frac{1}{N}\sum_{i=1}^{N} \left(\frac{1}{2}\|f_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)};\mathbf{y}^{(i)}\right)\|_2^2-\log\left|\det\mathbf{J}_{f_{\boldsymbol{\theta}}}\right|\right). \label{eq-cnf} \end{equation} \] Here, \(f_{\boldsymbol{\theta}}\) is the CNF with network parameters, \(\boldsymbol{\theta}\), and Jacobian, \(\mathbf{J}_{f_{\boldsymbol{\theta}}}\). It transforms each velocity model, \(\mathbf{x}^{(i)}\), into white noise (as indicated by the \(\ell_2\)-norm), conditioned on the observation, \(\mathbf{y}^{(i)}\). After training, the inverse of CNF turns random realizations of the standard Gaussian distribution into posterior samples (migration-velocity models) conditioned on any seismic observation that is in the same statistical distribution as the training data.

Physics-informed summary statistics

While CNFs are capable of approximating the posterior distribution, training the CNFs on pairs \(\left(\mathbf{x},\,\mathbf{y}\right)\) presents challenges when changes in the acquisition occur or when physical principles simplifying the mapping between model and data are lacking, both of which lead to increasing training costs. To tackle these challenges, S. T. Radev et al. (2022) introduced fixed reduced-size summary statistics that encapsulate observed data and inform the posterior distribution. Building on this concept, Orozco et al. (2023a) uses the gradient as the set of physics-informed summary statistics, partially reversing the forward map and therefore accelerating CNF training. For linear inverse problems with Gaussian noise, these statistics are unbiased — maintaining the same posterior distribution, whether conditioned on original shot data or on the gradient. Based on this principle, Siahkoohi et al. (2023) used reverse-time migration (RTM), given by the action of the adjoint of the linearized Born modeling, to summarize data and quantify imaging uncertainties for a fixed accurate migration-velocity model.

We aim to extend this approach to the nonlinear FWI problems. While RTM transfers information from the data to the image domain, its performance diminishes for incorrect migration velocities. Hou and Symes (2016) showed that least-squares migration can perfectly fit the data for correct migration-velocity models, but this fit fails for inaccurate velocity models. This highlights a fundamental limitation in cases where the velocity model is inaccurate and RTM does not correctly summarize the original shot data, which leads to a biased posterior. For an inaccurate initial FWI-velocity model \(\mathbf{x}_0\), \(p\left(\mathbf{x}\middle|\mathbf{y}\right) \neq p\left(\mathbf{x}\middle|\nabla\mathcal{F}\left(\mathbf{x}_0\right)^\top \mathbf{y}\right)\) with \(\nabla\mathcal{F}\) Born modeling and \(^\top\) the adjoint. To avoid this problem, more robust physics-informed summary statistics are needed to preserve information.

Common-image gathers as summary statistics

Migration-velocity analysis has a rich history in the literature (W. W. Symes, 2008). Following Hou and Symes (2016), we employ relatively artifact-free subsurface-offset extended Born modeling to calculate summary statistics. Because it is closer to an isometry—i.e, the adjoint of extended Born modeling is closer to its inverse (Yang et al., 2021; Kroode, 2023) and therefore preserves information — its adjoint can nullify residuals even when the FWI-velocity model is incorrect as shown by Hou and Symes (2016). Geng et al. (2022) further demonstrate that neural networks can be used to map CIGs to velocity models. Both these findings shed important light on the role of CIGs during VI because CIGs preserve more information than the gradient, which leads to less biased physics-informed summary statistics when given an inaccurate initial FWI-velocity model. Formally, this means \(p\left(\mathbf{x}\middle|\mathbf{y}\right) \approx p\left(\mathbf{x}\middle|\overline{\nabla\mathcal{F}}\left(\mathbf{x}_0\right)^\top \mathbf{y}\right)\), where \(\overline{\nabla\mathcal{F}}\) is extended Born modeling. Leveraging this mathematical observation, we propose WISE, short for full-Waveform variational Inference via Subsurface Extensions. The core of this technique is to train CNFs with pairs of velocity models, \(\mathbf{x}\), and CIGs, \(\overline{\nabla\mathcal{F}}\left(\mathbf{x}_0\right)^\top \mathbf{y}\), guided by the objective of Equation \(\ref{eq-cnf}\). Our case studies will demonstrate that even with inaccurate initial FWI-velocity models, CIGs encapsulate more information, enabling the trained CNFs to generate accurate migration-velocity models consistent with the observed shot data.

Synthetic case studies

Our study evaluates the performance of WISE through synthetic case studies on 2D slices of the Compass dataset (Jones et al., 2012), known for its “velocity kickback” challenge for FWI algorithms. For a poor initial FWI-velocity model, we aim to compare the quality of posterior samples informed by RTM alone versus those informed by CIGs to verify the superior information content of CIGs. We also illustrate how uncertainty in migration-velocity models can be converted into uncertainties in amplitude and positioning of imaged reflectors.

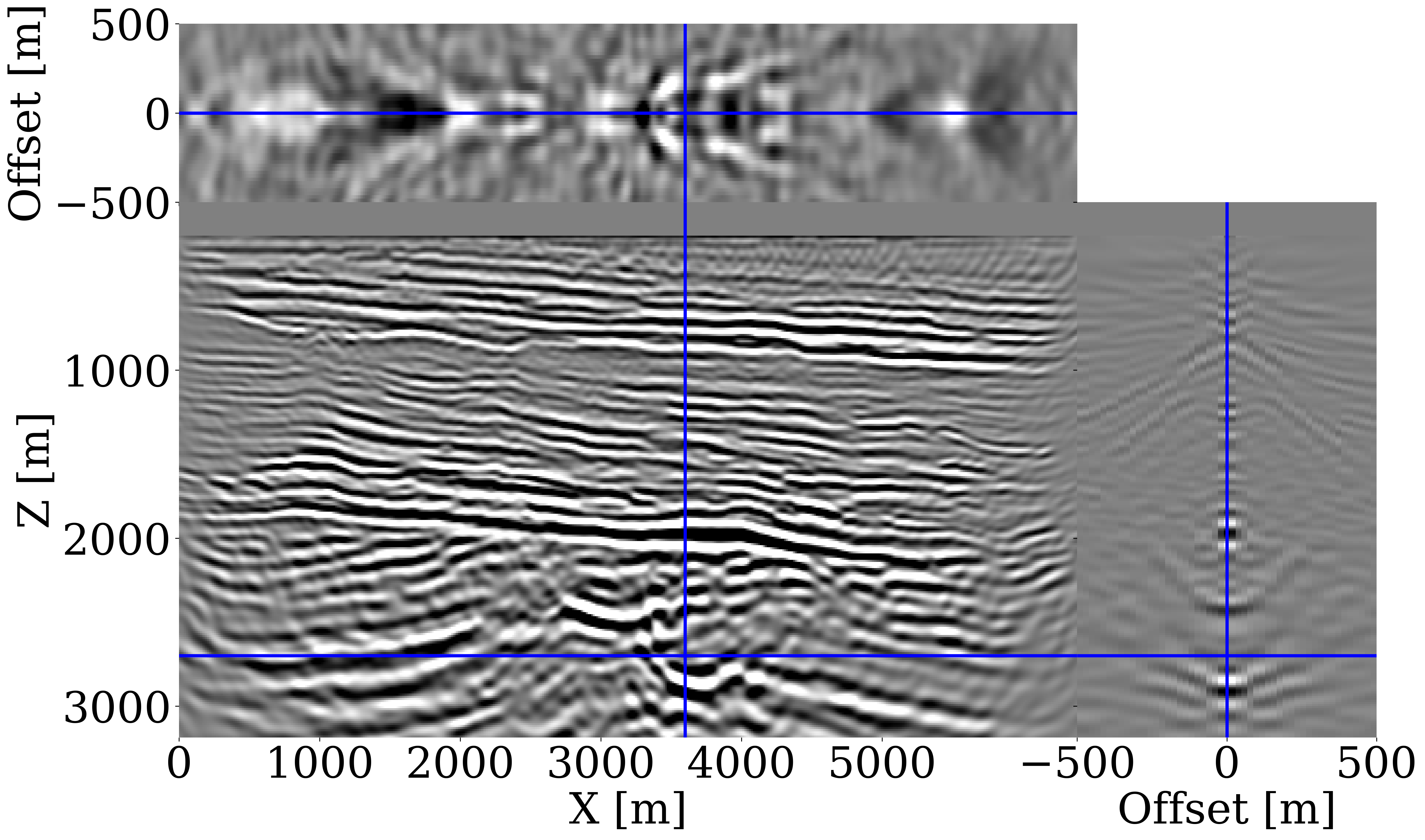
Dataset generation and network training. We take \(800\) 2D slices of the Compass model of \(6.4\) km by \(3.2\) km, with \(512\) equally spaced sources towed at \(12.5\mathrm{m}\) depth and \(64\) ocean-bottom nodes (OBNs) located at jittered sampled horizontal positions (Hennenfent and Herrmann, 2008; Herrmann, 2010). This sampling scheme utilizes compressive sensing techniques to improve acquisition productivity in various situations (Wason and Herrmann, 2013; Oghenekohwo et al., 2017; Wason et al., 2017; Yin et al., 2023). The surface is assumed absorbing. Using a \(15\mathrm{Hz}\) central frequency Ricker wavelet with energy below \(3\mathrm{Hz}\) removed for realism, acoustic data is simulated with Devito (M. Louboutin et al., 2019; F. Luporini et al., 2020) and JUDI.jl (Witte et al., 2019). Uncorrelated band-limited Gaussian noise is added (S/N \(12\mathrm{dB}\)). The arithmetic mean over all velocity models is used as the 1D initial FWI-velocity model (shown in Figure 1(b)). \(51\) horizontal subsurface offsets ranging from \(-500\mathrm{m}\) to \(+500\mathrm{m}\) are used to compute CIGs (shown in Figure 1(e)). Each offset is input to the network as a separate channel. We use the conditional glow network structure (Orozco et al., 2023b) for the CNFs because of its capability to generate superior natural (Durk P Kingma and Dhariwal, 2018) and seismic (Louboutin et al., 2023) images.

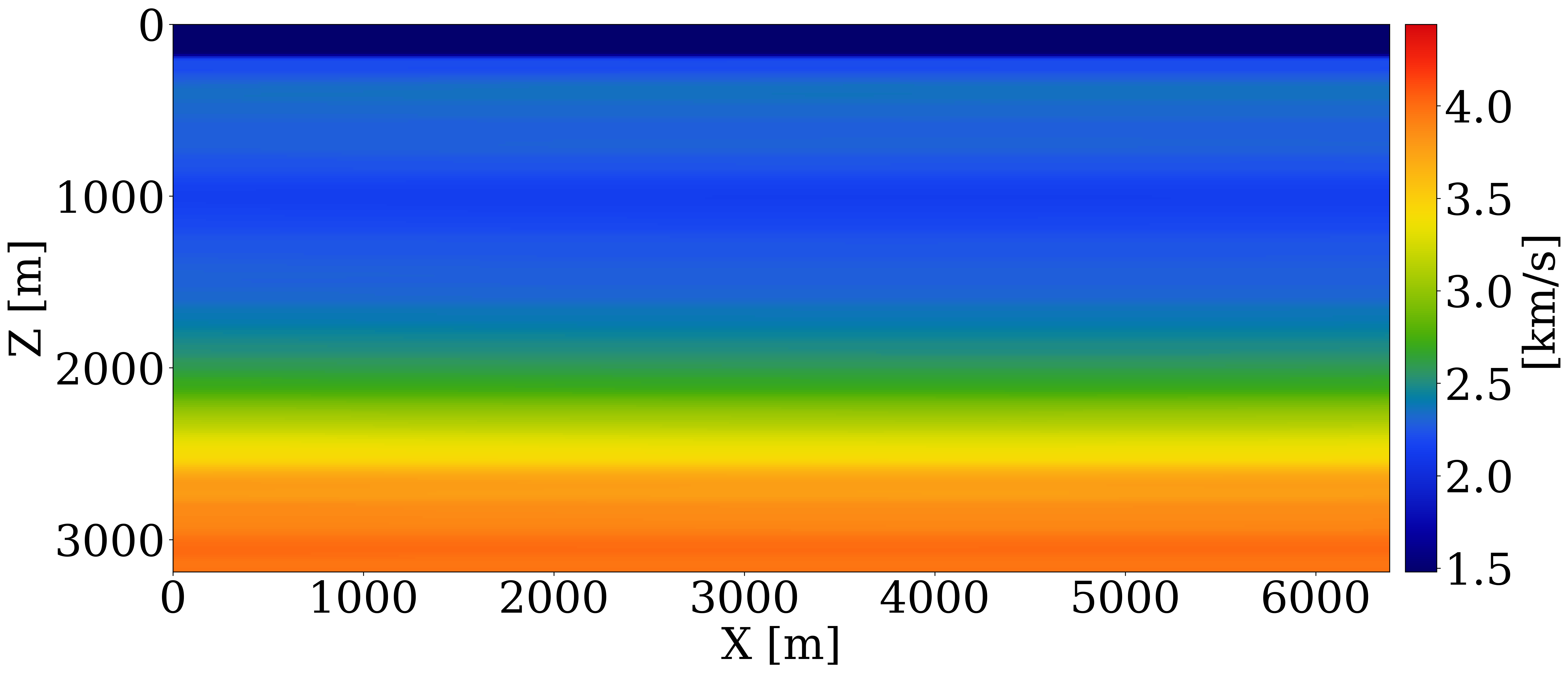
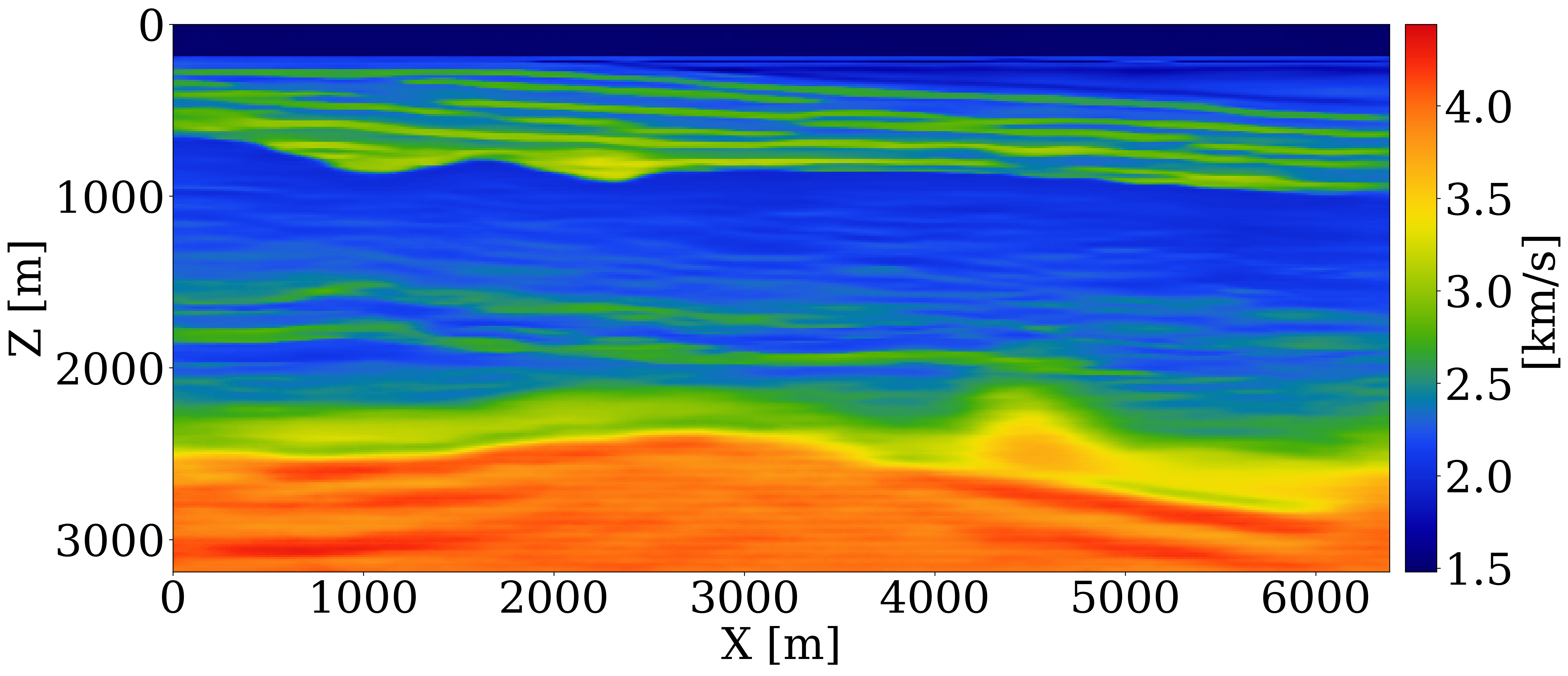
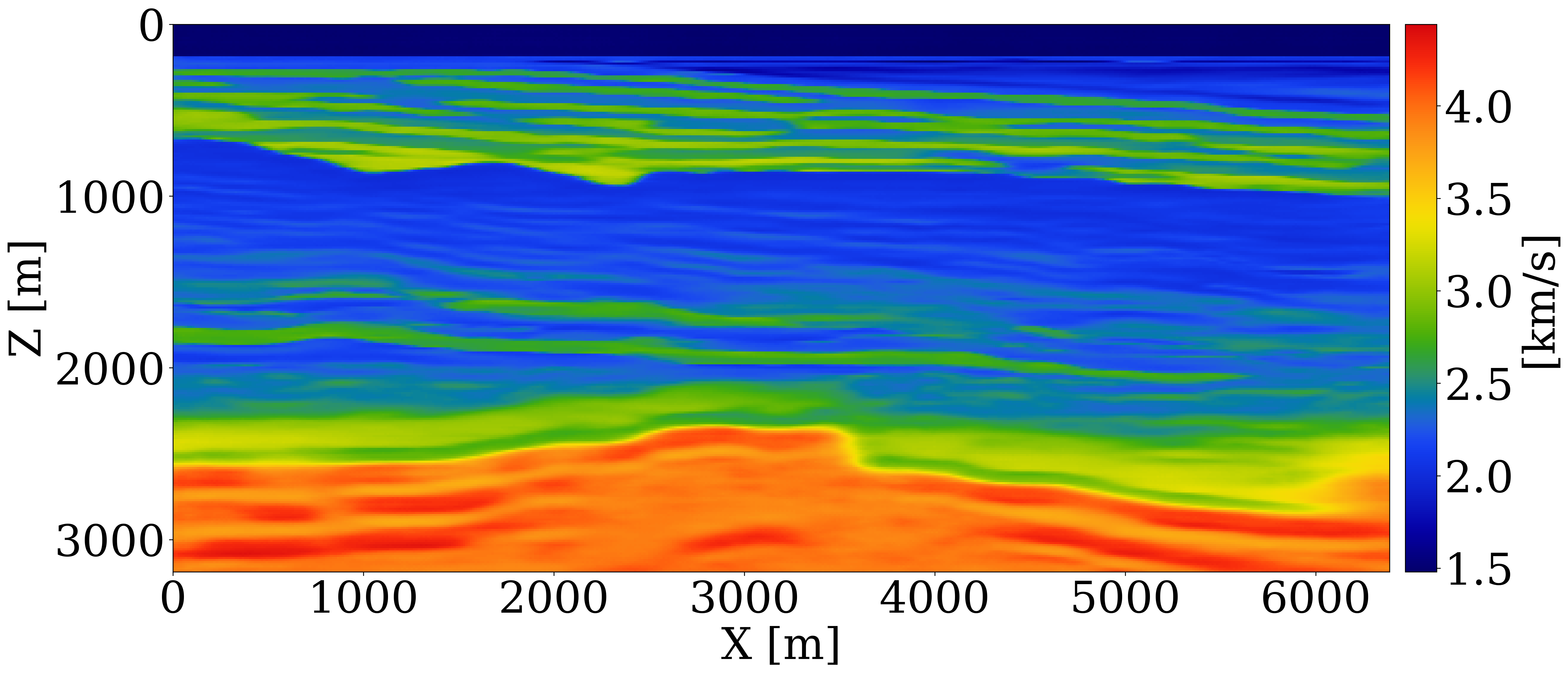
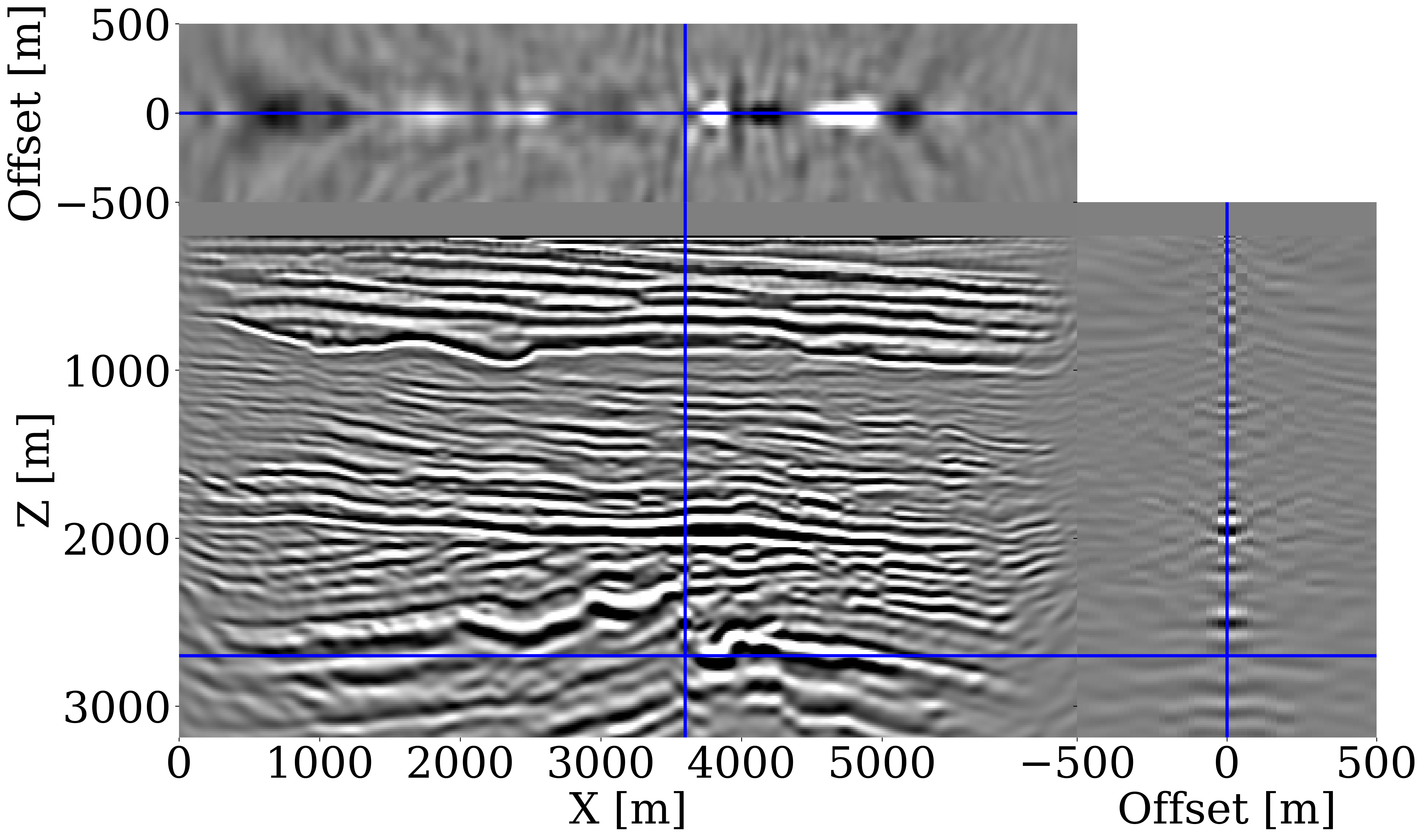
Results. After CNF training, our method’s performance is evaluated on an unseen 2D Compass slice shown in Figure 1(a). When RTM is used to summarize the data, the conditional mean estimate (Figure 1(c)) does not capture the shape of the unconformity. Thanks to the CIGs, WISE captures more information and as a result produces a more accurate conditional mean (Figure 1(d)). For the \(50\) test samples, the structural similarity index measure (SSIM) with CIGs yields a mean of \(0.63\), outperforming RTM-based statistics with a mean SSIM of \(0.52\).

Quality control. To verify the inferred migration-velocity model as the conditional mean of the posterior, CIGs calculated for the initial FWI-velocity model (Figure 1(b)), plotted in Figure 1(e), are juxtaposed against CIGs calculated for the inferred migration-velocity model (Figure 1(d)), plotted in Figure 1(f). Significant improvement in near-offset focused energy is observed in the CIGs for the inferred migration-velocity model. A similar focusing behavior is noted for the posterior samples themselves, as shown in the ancillary material.

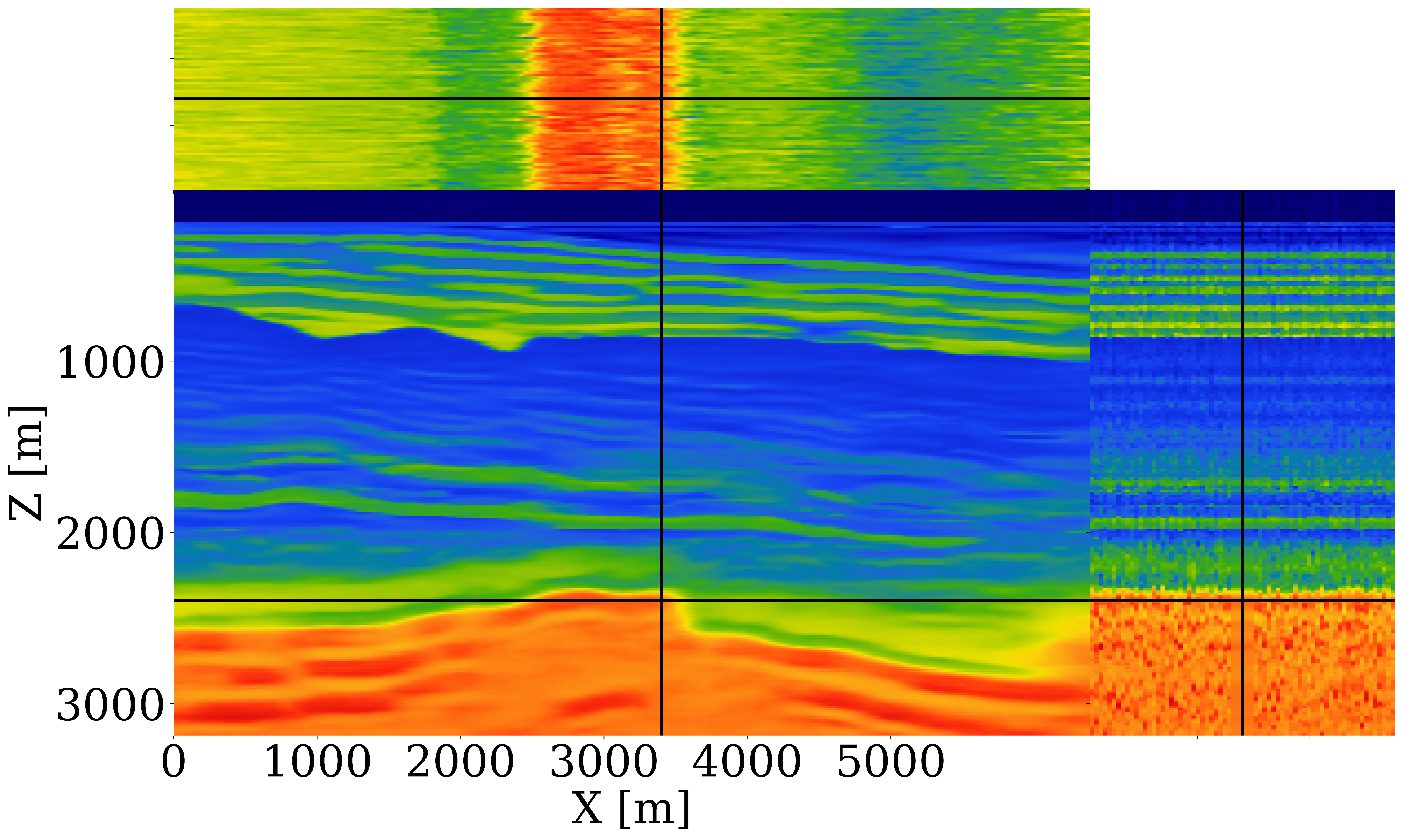
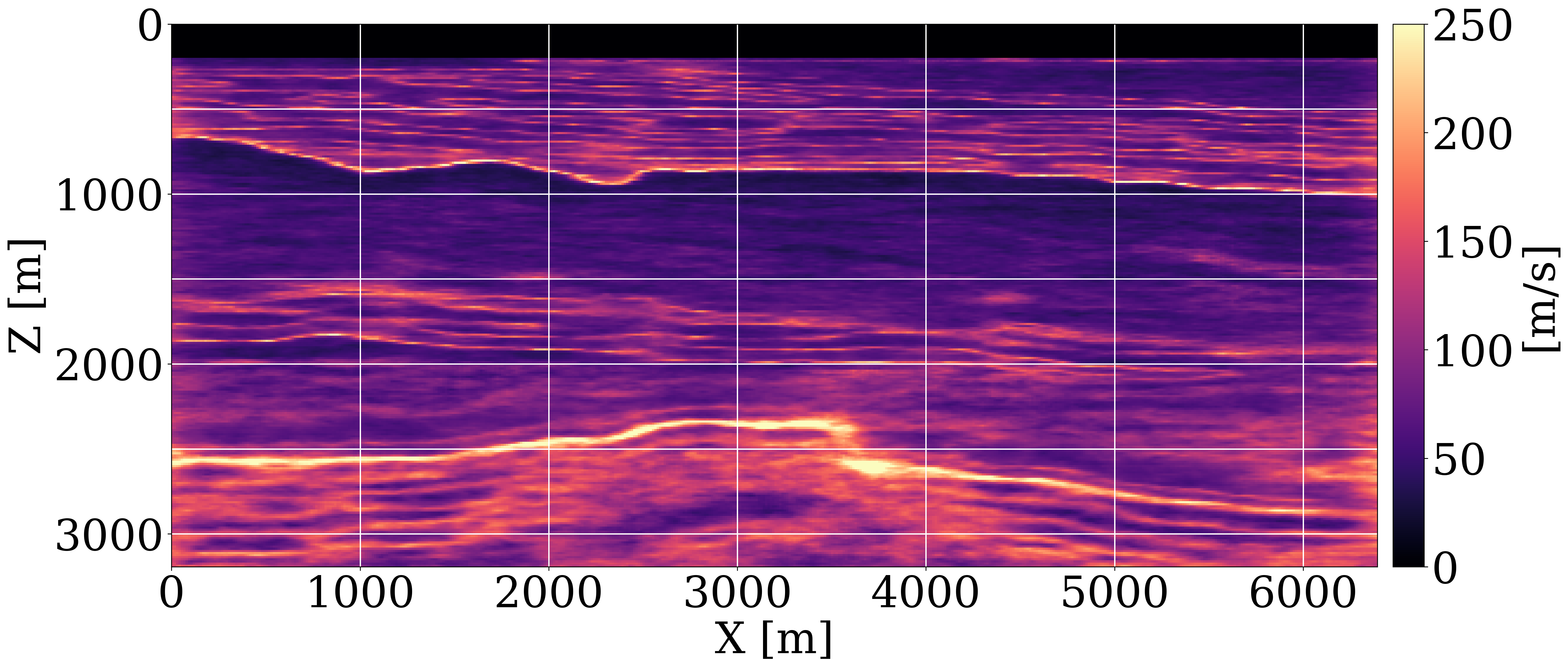
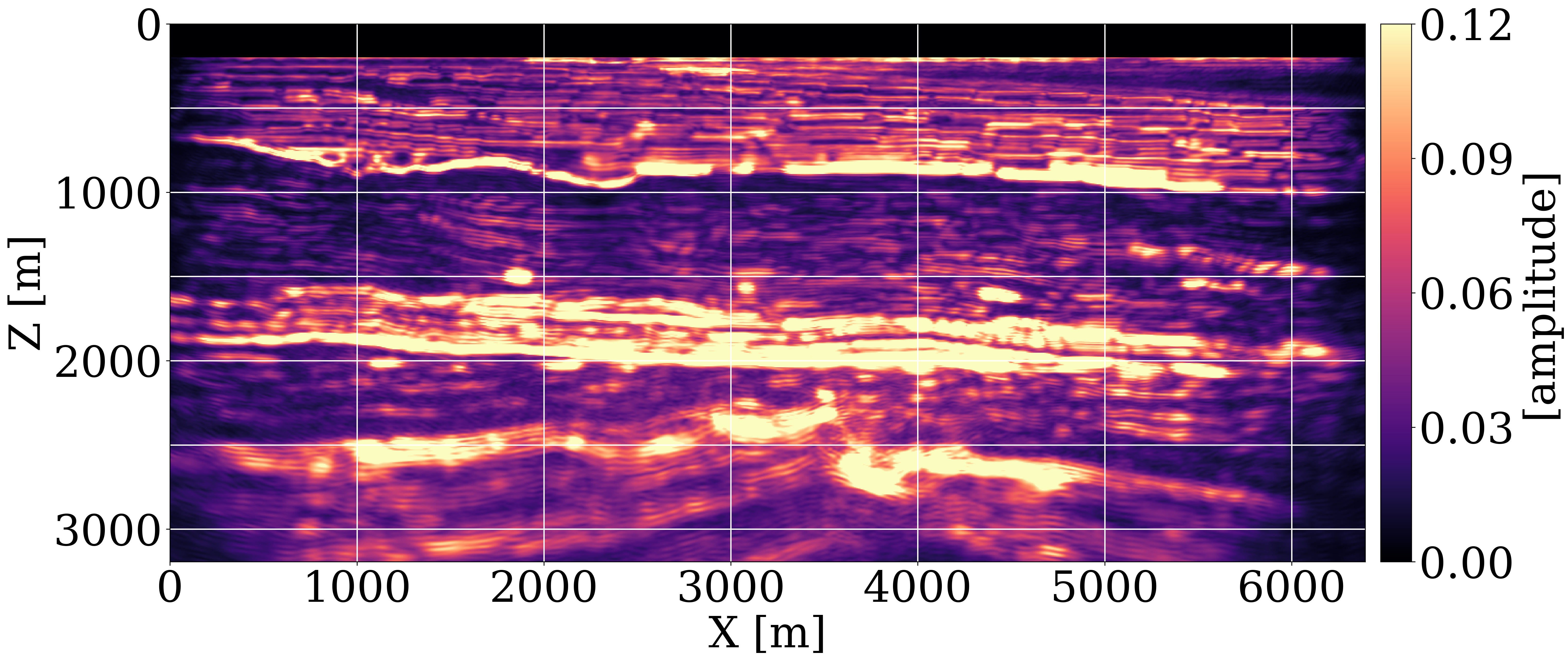
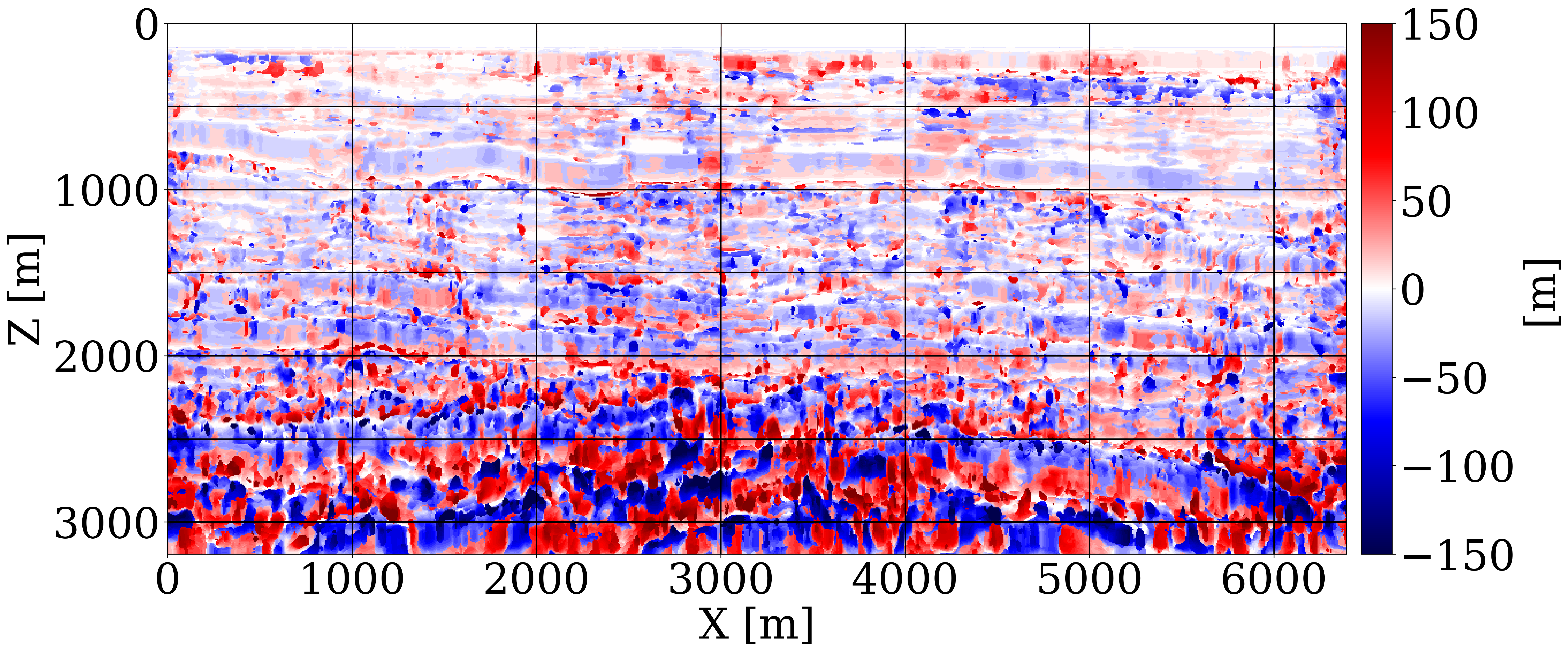
Uncertainty quantification and downstream imaging. While access to the posterior represents an important step towards grasping uncertainty, understanding its impact on imaging with (\(30\mathrm{Hz}\)) RTMs is more relevant because it concerns uncertainty in the final product. For this purpose, we display the posterior velocity samples in Figure 2(a) and the point-wise standard deviation in Figure 2(b). These deviations increase with depth and correlate with complex geology where the RTM-based inference struggled. To understand how this uncertainty propagates to imaged reflectors, forward uncertainty is assessed by carrying out RTMs for different posterior samples with results shown in Figure 2(c) and the standard deviations plotted in Figure 2(d). These amplitude deviations are different because mapping migration-velocities to RTMs is highly nonlinear, leading to large areas of intense amplitude variation and dimming at the edges caused by the Born modeling’s null-space. While these amplitude sensitivities are useful, deviations in the migration velocities also leads to differences in reflector positioning. Vertical shifts between the envelope of the reference image (central image in Figure 2(c)) and the envelopes of RTMs for different posterior samples are calculated with a local cross-correlation technique and included in Figure 2(d) where blue/red areas correspond to up/down shifts. As expected, these shifts are most notable in the deeper regions and at the edges where velocity variations are the largest.

Discussion

Once the offline costs of computing 800 CIGs and network training are covered, WISE enables generation of velocity models for unseen seismic data at the low computational cost of a single set of CIGs for a poor initial FWI-velocity model. The Open FWI (Deng et al., 2022) case study in the ancillary material demonstrates WISE’s capability to produce realistic posterior samples and conditional means for a broad range of unseen velocity models. In the case of the Compass model, the initial FWI-velocity model was poor. Still, CIGs obtained from a single 1D initial model capture relevant information from the non-zero offsets. From this information, the network learns to produce migration-velocity models that focus CIGs. WISE also produced two types of uncertainty, namely (i) inverse uncertainty in migration-velocity model estimation, which arises from both the non-trivial null-space of FWI and the measurement noise, and (ii) forward uncertainty where uncertainty in migration-velocity models is propagated to uncertainty in amplitude and positioning of imaged reflectors.

Opportunities for future research remain. One area concerns dealing with the “amortization gap” where CNFs tend to maximize performance across multiple datasets rather than excelling at a single observation (Marino et al., 2018). While we discovered that training CNFs on a diverse set of samples enhances generalization, applying AI techniques to unseen, out-of-distribution samples remains a challenge. However, our WISE framework is compatible with several fine-tuning approaches. To improve single-observation performance, particularly for out-of-distribution samples, computationally more expensive latent space corrections (Siahkoohi et al., 2023) can be employed that incorporate the physics. Recent studies also have indicated that trained CNFs can act as preconditioners or regularizers for physics-based, non-amortized inference (Rizzuti et al., 2020; Siahkoohi et al., 2021). These correction methods can enhance the fit of posterior samples to observed data, as shown in Siahkoohi et al. (2023), or enable the generation of more focused CIGs through migration velocity analysis. Moreover, velocity continuation methods (Fomel, 2003) could be used including recent advances in neural operators (Siahkoohi et al., 2022). These could offset the cost of running RTMs for each posterior sample, thus accelerating forward uncertainty propagation. While we observed that providing more offsets can enhance the quality of the inference, we recognize the resulting increase in CIG computation costs and CNF memory consumption. This necessitates cost-effective frameworks for determining optimal offset numbers or sampling strategies for CIGs. In this context, recent work on using CNFs for Bayesian optimal experimental design (Orozco et al., 2024) seamlessly integrates as an advancement to the WISE framework. Considering low-rank approximations of CIGs (Yang et al., 2021) may reduce computational demands. Additionally, exploring other conditional generative models like diffusion models (Baldassari et al., 2024) may be worthwhile. Our case studies have yet to account for inverse uncertainty due to modeling errors, such as attenuation effects, multiples, or residual shear wave energy, which could be addressed through Bayesian model misspecification techniques (Schmitt et al., 2023). Recent advances suggest that transfer learning could correct these modeling inaccuracies (Siahkoohi et al., 2019; Yao et al., 2023), a solution that our approach is amenable to.

Incurred computational cost on an NVIDIA A100 GPU can be broken down as follows: generating training pairs requires generation of 64 OBN datasets and corresponding CIGs for 800 models, totaling approximately 80 hours of runtime. After generating the training set, training the CNF takes around 16 hours. With these initial runtime investments, the cost for a single inference involves only a single CIG computation, which takes about 6 minutes. For context, running a single FWI starting from the velocity model included in Figure 1(b) requires 12.5 data passes taking roughly 50 minutes to complete (the final result is shown in the ancillary material). Traditional UQ methods require the compute equivalent to hundreds of FWI runs (X. Zhang et al., 2023), but here we estimate at least 50 FWI runs. Based on these numbers, the computational savings from employing CNF surrogates offset the upfront costs after inference on approximately 3 datasets. We emphasize that as long as the statistics of the underlying geology remains similar, our amortized network can be applied to different observed datasets in the complete basin without retraining. Furthermore, the parallel execution of training pair generation on clusters can significantly reduce initial computational time. Although our study primarily demonstrates a proof of concept on a realistic 2D experiment, the WISE software tool chain is designed for large-scale 3D problems. CNFs, favored for their memory efficiency through invertibility (Orozco et al., 2023b), are well-suited for 3D problems. In addition, memory consumption of CIG computation can be reduced significantly with random trace estimation techniques (Louboutin and Herrmann, 2024). Since our work requires training samples of Earth models, we envision these samples coming from legacy proxy models and future work will explore automatic workflows for generating these from field observations.

Conclusions

We present WISE, full-Waveform variational Inference via Subsurface Extensions, for computationally efficient uncertainty quantification of FWI. This framework underscores the potential of generative AI to address FWI challenges, paving the way for a new seismic inversion and imaging paradigm that is uncertainty-aware. By having common-image gathers act as information-preserving summary statistics, a principled approach to UQ is achieved where generative AI is successfully combined with wave physics. Because WISE automatically produces distributions for migration-velocity models conditioned by the data, it moves well beyond traditional velocity model building. It was shown that this distributional information can be employed to quantify uncertainties in the migration-velocity models that can be used to better understand amplitude and positioning uncertainty in migration.

Acknowledgements

This research was carried out with the support of Georgia Research Alliance and partners of the ML4Seismic Center. The authors would like to thank Charles Jones (Osokey) for the constructive discussion.

Declaration of generative AI and AI-assisted technologies in the writing process

During the preparation of this work, the authors used ChatGPT to improve readability and language. After using this service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.