Source separation for simultaneous towed-streamer marine acquisition—a compressed sensing approach

Rajiv Kumar^*, Haneet Wason^* and Felix J. Herrmann
Seismic Laboratory for Imaging and Modeling (SLIM), The University of British Columbia, Canada
^* Equal contributors

Introduction

The benefits of simultaneous source marine acquisition are manifold—it allows the acquisition of improved-quality seismic data at standard (conventional) acquisition turnaround, or a reduced turnaround time while maintaining similar quality, or a combination of both advantages. In simultaneous marine acquisition, a single and/or multiple source vessels fire sources at near-simultaneous or slightly random times resulting in overlapping shot records (Kok and Gillespie, 2002; Beasley, 2008; Berkhout, 2008; Hampson et al., 2008; N Moldoveanu and Quigley, 2011; Abma et al., 2013), as opposed to non-overlapping shot records in conventional marine acquisition. Variety of simultaneous source survey designs have been proposed for towed-streamer and ocean bottom acquisitions, where small-to-large random time delays between multiple sources have been used (Beasley, 2008; Nicolae Moldoveanu and Fealy, 2010; Mansour et al., 2012; Abma et al., 2013; Wason and Herrmann, 2013b; Mosher et al., 2014).

An instance of low-variability in source firing times—e.g., \(\leq\) 1 (or 2) second, is the over/under (or multi-level) source acquisition (Hill et al., 2006; Nick Moldoveanu et al., 2007; Lansley et al., 2007; A. Long, 2009; Hegna and Parkes, 2012; Torben Hoy, 2013). The benefits of acquiring and processing over/under data are clear, the recorded bandwidth is extended at both low and high ends of the spectrum since the depths of the sources produce complementary ghost functions, avoiding deep notches in the spectrum. The over/under acquisition allows separation of the up- and down-going wavefields at the source (or receiver) using a vertical pair of sources (or receivers) to determine wave direction. Simultaneous long offset acquisition (SLO) is another variation of simultaneous towed-streamer acquisition, where an extra source vessel is deployed, sailing one spread-length ahead of the main seismic vessel (A. S. Long et al., 2013, and the references therein). The SLO technique is better in comparison to conventional acquisition since it provides longer coverage in offsets, less equipment downtime (doubling the vessel count inherently reduces the streamer length by half), easier maneuvering, and shorter line turns.

Simultaneous acquisition (e.g., over/under and SLO) results in seismic interferences or source crosstalk that degrades quality of the migrated images. Therefore, effective (simultaneous) source separation techniques are required, which aim to recover unblended interference-free data—as acquired during conventional acquisition—from simultaneous data. The challenge of source separation (or deblending) has been addressed by many researchers (Stefani et al., 2007; Moore et al., 2008; Akerberg et al., 2008; Huo et al., 2009), wherein the key observation has been that as long as the sources are fired at suitably randomly dithered times, the resulting interferences (or source crosstalk) will appear noise-like in specific gather domains such as common-offset and common-receiver, turning the separation problem into a (random) noise removal procedure. Inversion-type algorithms (Moore, 2010; Abma et al., 2010; Mahdad et al., 2011; Doulgeris et al., 2012; Baardman and Borselen, 2013) take advantage of sparse representations of coherent seismic signals. Wason and Herrmann (2013a); Wason and Herrmann (2013b) proposed an alternate sampling strategy for simultaneous acquisition (time-jittered marine) that leverages ideas from compressed sensing (CS), addressing the deblending problem through a combination of tailored (blended) acquisition design and sparsity-promoting recovery via convex optimization using \(\ell_1\) constraints. This represents a scenario of high-variability in source firing times—e.g., \(>\) 1 second, resulting in irregular shot locations.

One of the source separation techniques is the normal moveout based median filtering, where the key idea is as follows: \(i)\) transform the blended data into the midpoint-offset domain, \(ii)\) perform semblance analysis on common-midpoint gathers to pick the normal moveout (NMO) velocities followed by NMO corrections, \(iii)\) perform median filtering along the offset directions and then apply inverse NMO corrections. One of the major assumptions in the described workflow is that the seismic events become flat after NMO corrections, however, this can be challenging when the geology is complex and/or with the presence of noise in the data. Therefore, the above process along with the velocity analysis is repeated a couple of times to get a good velocity model to eventually separate simultaneous data.

Recently, rank-minimization based techniques have been used for source separation by Maraschini et al. (2012) and Cheng and Sacchi (2013). The general idea is to exploit the low-rank structure of seismic data when it is organized in a matrix. Low-rank structure refers to the small number of nonzero singular values, or quickly decaying singular values. Maraschini et al. (2012) followed the rank-minimization based approach proposed by Oropeza and Sacchi (2011), who identified that seismic temporal frequency slices organized into a block Hankel matrix, in ideal conditions, is a matrix of rank \(k\), where \(k\) is the number of different plane waves in the window of analysis. Oropeza and Sacchi (2011) showed that additive random noise increase the rank of the block Hankel matrix and presented an iterative algorithm that resembles seismic data reconstruction with the method of projection onto convex sets, where they use a low-rank approximation of the Hankel matrix via the randomized singular value decomposition (Liberty et al., 2007; Halko et al., 2011a) to interpolate seismic temporal frequency slices. While this technique may be effective the approach requires embedding the data into an even larger space where each dimension of size \(n\) is mapped to a matrix of size \(n \times n\). Consequently, these approaches are applied on small data windows, where one has to choose the size of these windows. Although mathematically desirable due to the seismic signal being stationary in sufficiently small windows, Kumar et al. (2014) showed that the act of windowing from a matrix-rank point of view degrades the quality of reconstruction in the case of missing-trace interpolation. Choosing window sizes apriori is also a difficult task, as it is not altogether obvious how to ensure that the resulting sub-volume is approximately a plane-wave.

Motivation

The success of CS hinges on randomization of the acquisition, as presented in our previous work on simultaneous source acquisition (Mansour et al., 2012; Wason and Herrmann, 2013b), which represents a case of high-variability in source firing times—e.g., within a range of 1-20 seconds, resulting in overlapping shot records that lie on irregular spatial grids. Consequently, this made our method applicable to marine acquisition with ocean bottom cables/nodes. Successful separation of simultaneous data by sparse inversion via one-norm minimization, in this high-variability scenario, motivated us to analyze the performance of our separation algorithm for the low-variability, simultaneous towed-streamer acquisitions. In this paper, we address the challenge of source separation for two types of simultaneous towed-streamer marine acquisition—over/under and simultaneous long offset. We also compare the sparsity-promoting separation technique with separation via rank-minimization based technique, since the latter is relatively computationally faster and memory efficient, as shown by Kumar et al. (2014) for missing-trace interpolation.

Contributions

Our contributions in this work are the following: first, we propose a practical framework for source separation based upon the compressed sensing (CS) theory, where we outline the necessary conditions for separating the simultaneous towed-streamer data using sparsity-promoting and rank-minimization techniques. Second, we show that source separation using the rank-minimization based framework includes a “transform domain” where we exploit the low-rank structure of seismic data. We further establish that in simultaneous towed-streamer acquisition each monochromatic frequency slice of the fully sampled blended data matrix with periodic firing times has low-rank structure in the proposed transform domain. However, uniformly random firing-time delays increase the rank of the resulting frequency slice in this transform domain, which is a necessary condition for successful recovery via rank-minimization based techniques.

Third, we show that seismic frequency slices in the proposed transform domain exhibit low-rank structure at low frequencies, but not at high frequencies. Therefore, in order to exploit the low-rank structure at higher frequencies we adopt the Hierarchical Semi-Separable matrix representation (HSS) method proposed by Chandrasekaran et al. (2006) to represent frequency slices. Finally, we combine the (SVD-free) matrix factorization approach recently developed by Lee et al. (2010) with the Pareto curve approach proposed by Berg and Friedlander (2008). This renders the framework suitable for large-scale seismic data since it avoids the computation of the singular value decomposition (SVD), a necessary step in traditional rank-minimization based methods, which is prohibitively expensive for large matrices.

We simulate two simultaneous towed-streamer acquisitions—over/under and simultaneous long offset, and compare the recovery in terms of the separation quality, computational time and memory usage. In addition, we also make comparisons with the NMO-based median filtering type technique proposed by Y. Chen et al. (2014).

Theory

Compressed sensing is a signal processing technique that allows a signal to be sampled at sub-Nyquist rate and offers three fundamental principles for successful reconstruction of the original signal from relatively few measurements. The first principle utilizes the prior knowledge that the underlying signal of interest is sparse or compressible in some transform domain—i.e., if only a small number \(k\) of the transform coefficients are nonzero or if the signal can be well approximated by the \(k\) largest-in-magnitude transform coefficients. The second principle is based upon a sampling scheme that breaks the underlying structure—i.e., decreases the sparsity of the original signal in the transform domain. Once the above two principles hold, a sparsity-promoting optimization problem can be solved in order to recover the fully sampled signal. It is well known that seismic data admit sparse representations by curvelets that capture “wavefront sets” efficiently (see e.g., Smith (1998), Candès and Demanet (2005), Hennenfent and Herrmann (2006) and the references therein).

For high resolution data represented by the \(N\)-dimensional vector \(\mathbf{f}_0 \in \mathbb{R}^N\), which admits a sparse representation \(\mathbf{x}_0 \in \mathbb{C}^P\) in some transform domain characterized by the operator \(\mathbf{S} \in \mathbb{C}^{P\times N}\) with \(P \geq N\), the sparse recovery problem involves solving an underdetermined system of equations: \[ \begin{equation} \label{eq:linsystem} \mathbf{b} = \mathbf{Ax}_0, \end{equation} \] where \(\mathbf{b} \in \mathbb{C}^n\), \(n \ll N \leq P\), represents the compressively sampled data of \(n\) measurements, and \(\mathbf{A} \in \mathbb{C}^{n \times P}\) represents the measurement matrix. We denote by \(\mathbf{x}_0\) a sparse synthesis coefficient vector of \(\mathbf{f}_0\). When \(\mathbf{x}_0\) is strictly sparse—i.e., only \(k < n\) nonzero entries in \(\mathbf{x}_0\), sparsity-promoting recovery can be achieved by solving the \(\ell_0\) minimization problem, which is a combinatorial problem and quickly becomes intractable as the dimension increases. Instead, the basis pursuit denoise (BPDN\(_\epsilon\)) convex optimization problem: \[ \begin{equation} \label{eq:BPDN} \underset{\mathbf{x} \in \mathbb{C}^P}{\text{minimize}} \quad \|\mathbf{x}\|_1 \quad \textrm{subject to} \quad \|\mathbf{b} - \mathbf{Ax}\|_2 \leq \epsilon, \tag{BPDN$_\epsilon$} \end{equation} \] can be used to recover \(\mathbf{\tilde{x}}\), which is an estimate of \(\mathbf{x}_0\). Here, \(\epsilon\) represents the error-bound in the least-squares misfit and the \(\ell_1\) norm \(\|\mathbf{x}\|_1\) is the sum of absolute values of the elements of a vector \(\mathbf{x}\). The matrix \(\mathbf{A}\) can be composed of the product of an \(n \times N\) sampling (or acquisition) matrix \(\mathbf{M}\) and the sparsifying operator \(\mathbf{S}\) such that \(\mathbf{A} := \mathbf{MS}^H\), here \(^H\) denotes the Hermitian transpose. Consequently, the measurements are given by \(\mathbf{b} = \mathbf{A}\mathbf{x}_0 = \mathbf{Mf}_0.\) A seismic line with \(N_s\) sources, \(N_r\) receivers, and \(N_t\) time samples can be reshaped into an \(N\) dimensional vector \(\mathbf{f}\), where \(N = N_s \times N_r \times N_t\). For simultaneous towed-streamer acquisition, given two unblended data vectors \({{\mathbf{x}}_1}\) and \({{\mathbf{x}}_2}\) and (blended) measurements \(\mathbf{b}\), we can redefine Equation \(\ref{eq:linsystem}\) as \[ \begin{equation} \label{matrix} \begin{aligned} \overbrace{ \begin{bmatrix} {{\mathbf{MT_1}}}{\bf{\mathbf{S}}}^H & {{\mathbf{MT_2}}}{\bf{\mathbf{S}}}^H \end{bmatrix} }^{\mathbf{A}} \overbrace{ \begin{bmatrix} {\mathbf{x}}_1 \\ {\mathbf{x}}_2 \end{bmatrix} }^{\mathbf{x}} = {\mathbf{b}}, \end{aligned} \end{equation} \]
where \({\mathbf{T}}_1\) and \({\mathbf{T}}_2\) are defined as the firing-time delay operators which apply uniformly random time delays to the first and second source, respectively. Note that accurate knowledge of the firing times is essential for successful recovery by the proposed source separation techniques. We wish to recover a sparse approximation \({\mathbf{\tilde{f}}}\) of the discretized wavefield \(\mathbf{f}\) (corresponding to each source) from the measurements \(\mathbf{b}\). This is done by solving the BPDN\(_\epsilon\) sparsity-promoting program, using the SPG\(\ell_1\) solver (see Berg and Friedlander, 2008 for details), yielding \({\mathbf{\tilde{f}}}=\mathbf{S}^H \mathbb{\tilde{\mathbf{x}}}\) for each source.

Sparsity is not the only structure seismic data exhibits where three- or five-dimensional seismic data is organized as a vector. High-dimensional seismic data volumes can also be represented as matrices or tensors, where the low-rank structure of seismic data can be exploited (Trickett and Burroughs, 2009; Oropeza and Sacchi, 2011; Kreimer and Sacchi, 2012; Silva and Herrmann, 2013; Aravkin et al., 2014). This low-rank property of seismic data leads to the notion of matrix completion theory which offers a reconstruction strategy for an unknown matrix \(\mathbf{X}\) from its known subsets of entries (Candès and Recht, 2009; Recht et al., 2010a). The success of matrix completion framework hinges on the fact that regularly sampled target dataset should exhibit a low-rank structure in the rank-revealing “transform domain” while subsampling should destroy the low-rank structure of seismic data in the transform domain.

Rank-revealing “transform domain”

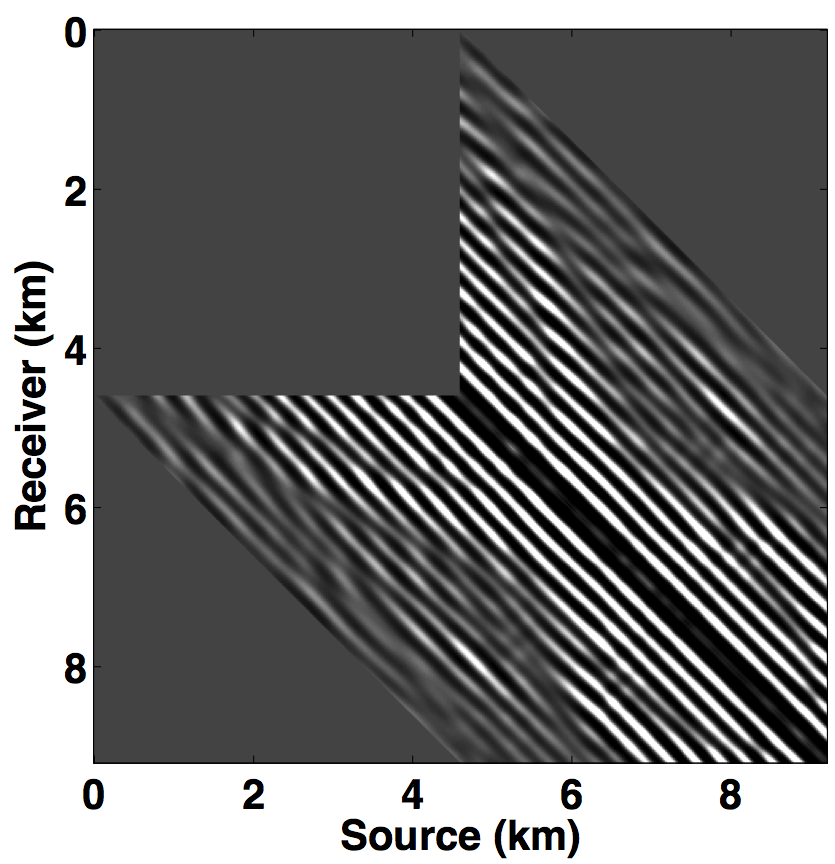
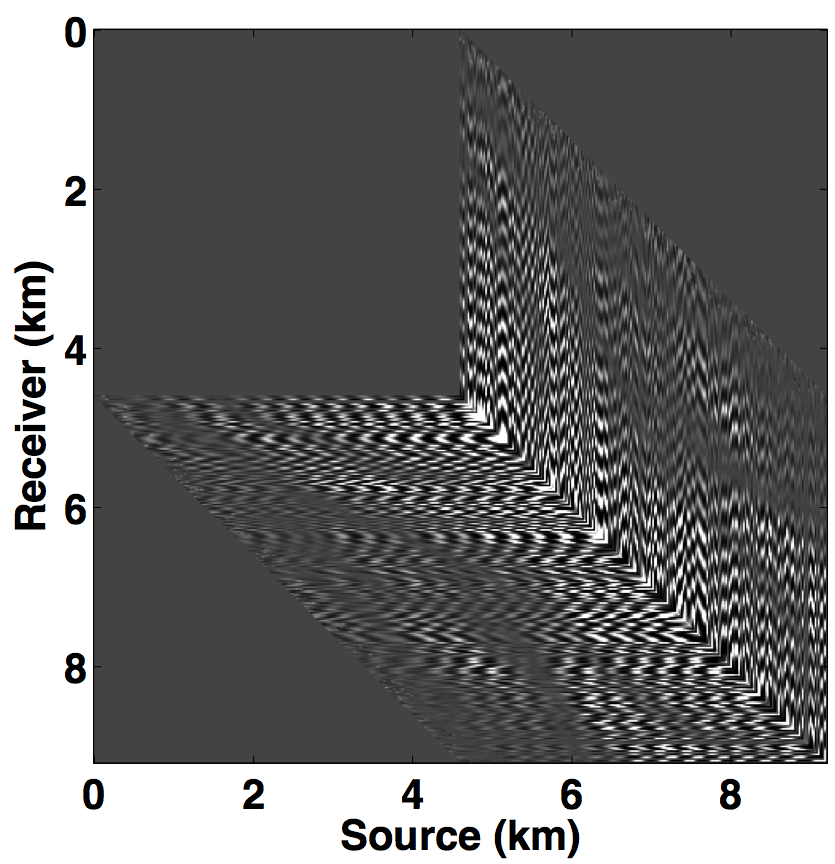
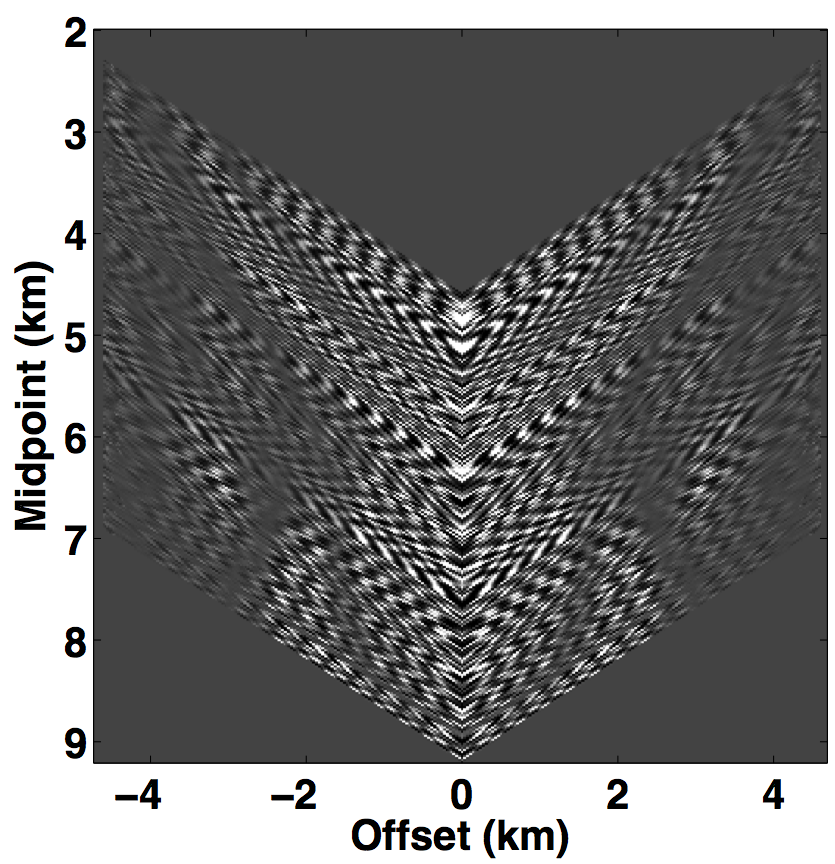
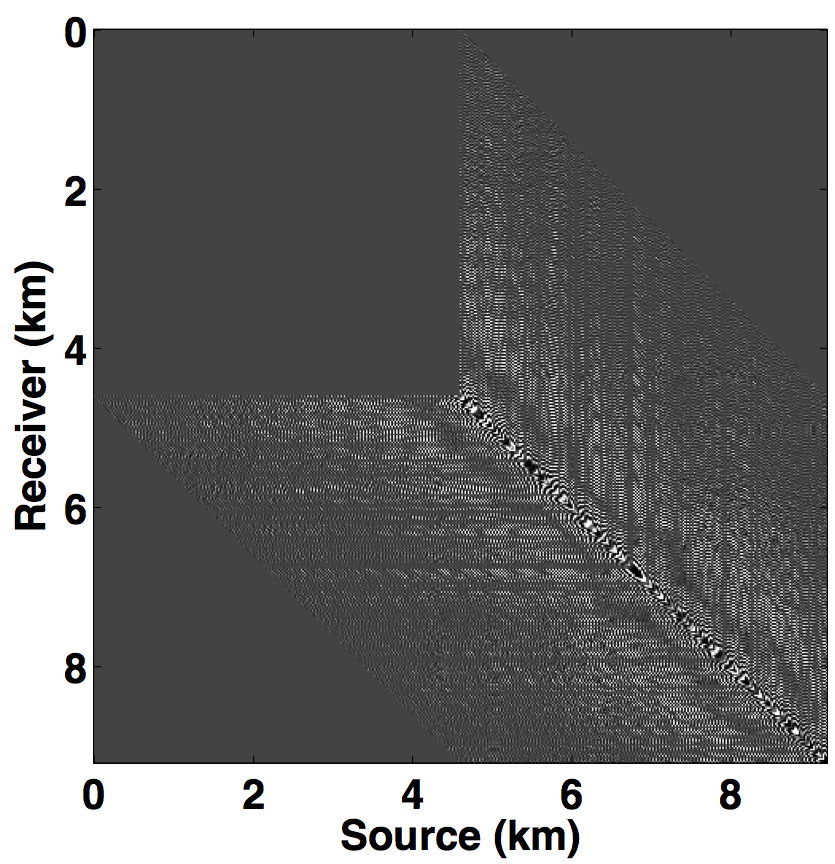
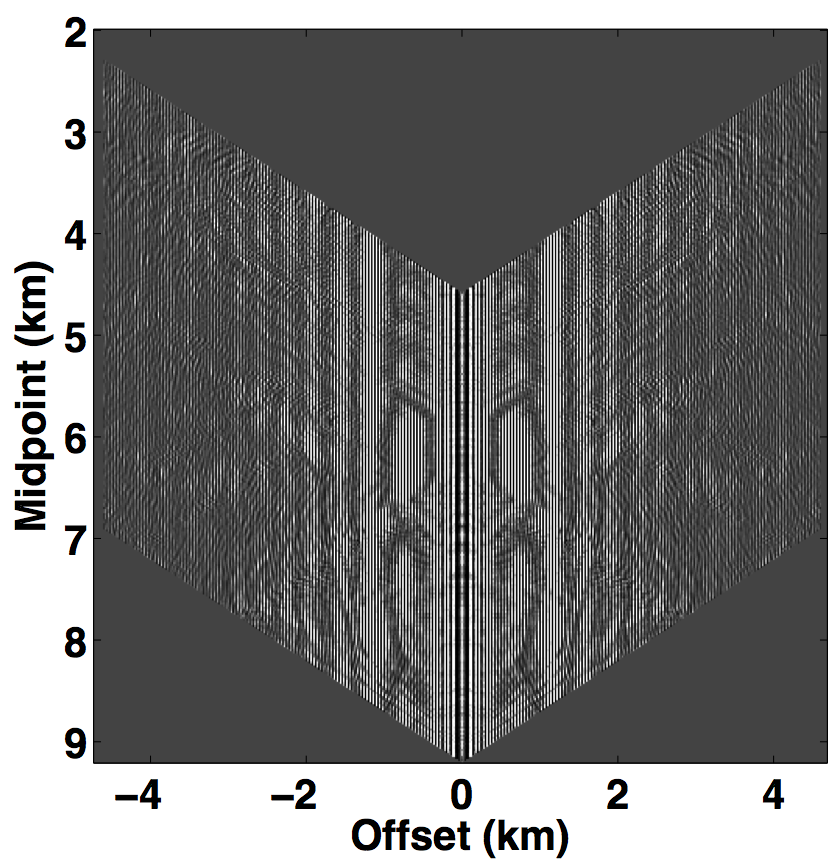
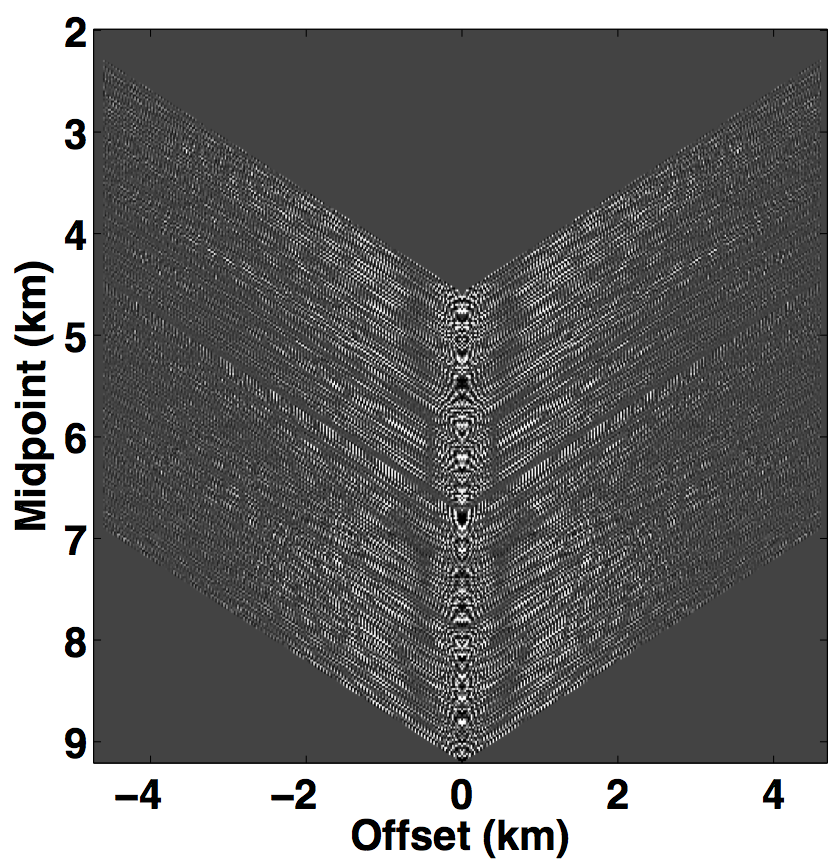
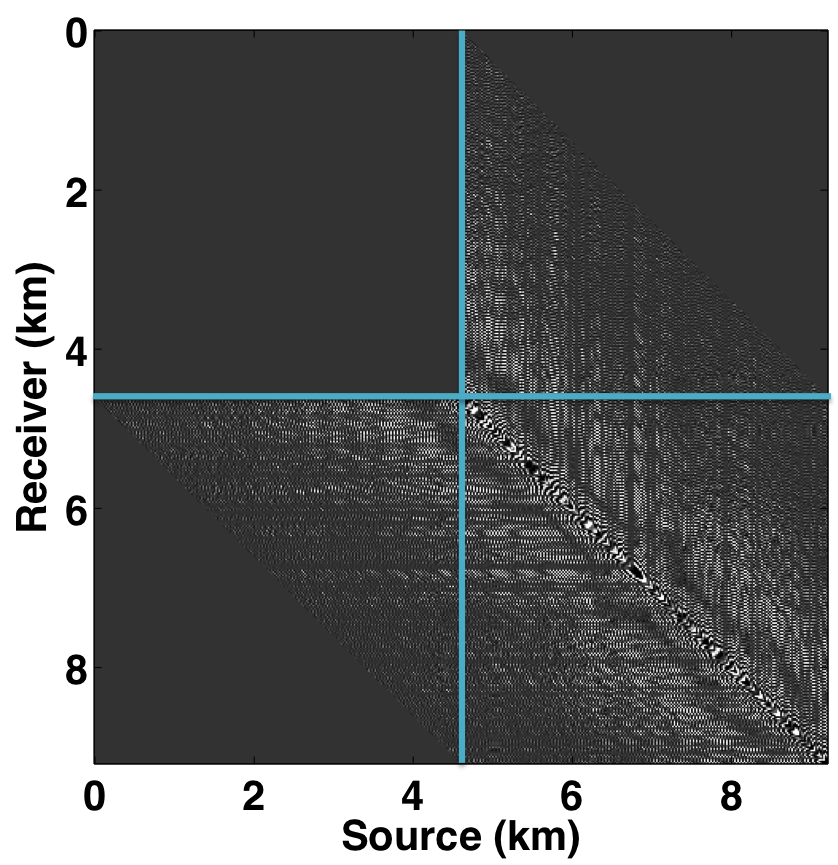
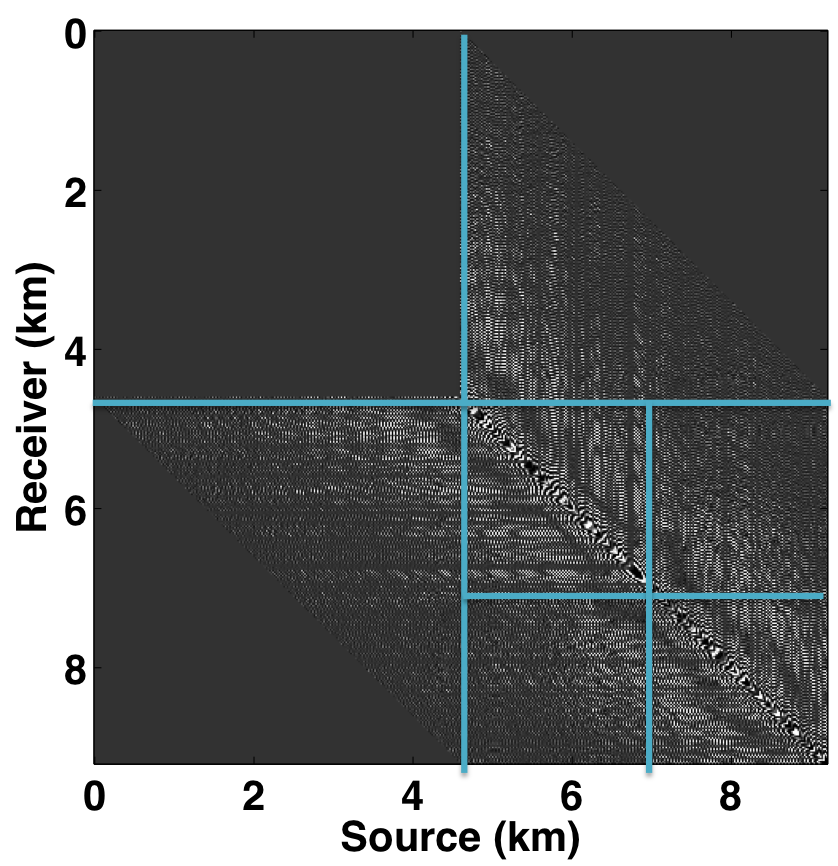
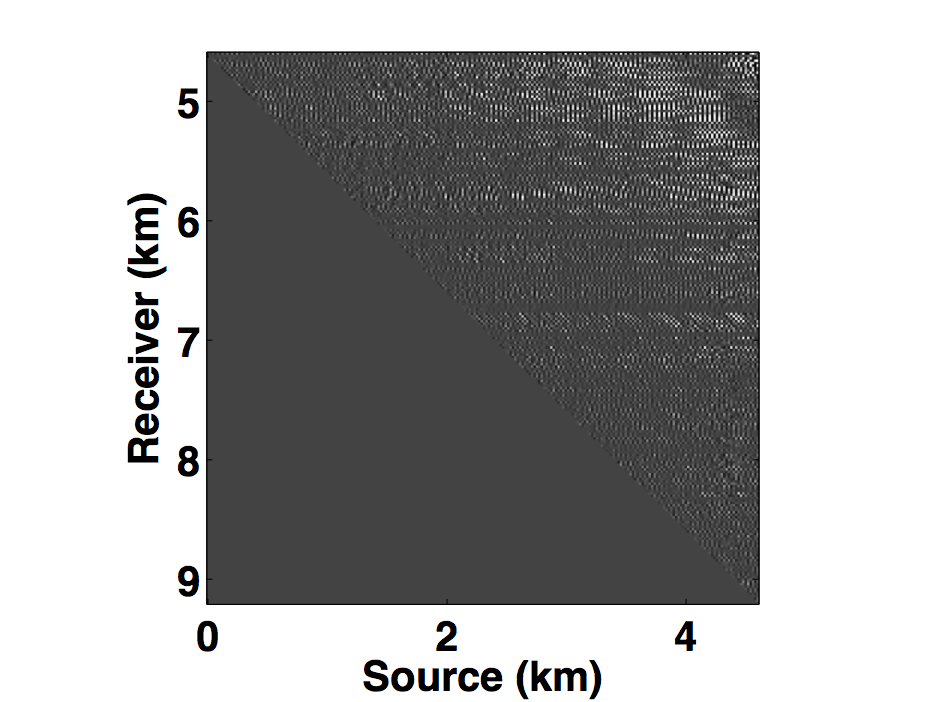
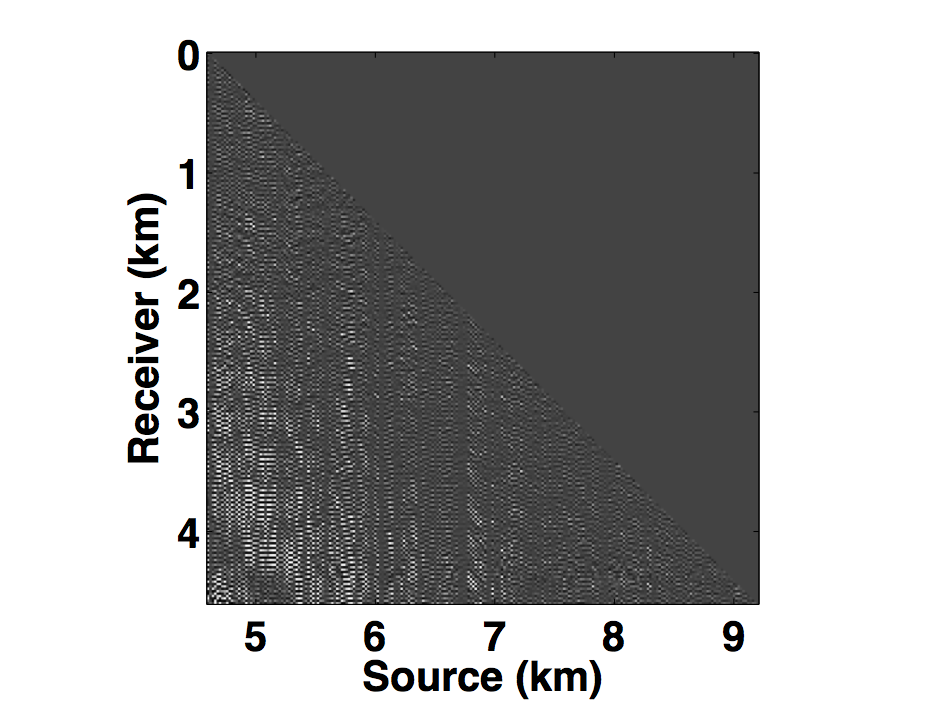
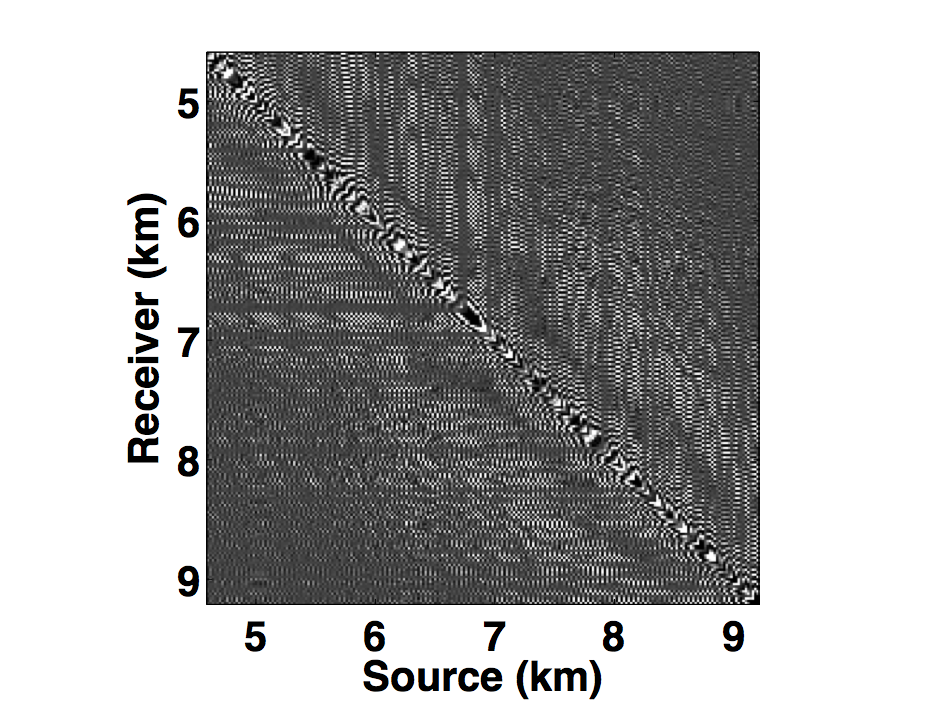
Following the same analogy of CS, the main challenge in applying matrix completion techniques to the source separation problem is to find a “transform domain” wherein: \(i)\) fully sampled conventional (or unblended) seismic data have low-rank structure—i.e., quickly decaying singular values; \(ii)\) blended seismic data have high-rank structure—i.e., slowly decaying singular values. When these properties hold, rank-minimization techniques (used in matrix completion) can be used to recover the deblended signal. Kumar et al. (2013) showed that the frequency slices of unblended seismic data do not exhibit low-rank structure in the source-receiver (s-r) domain since strong wavefronts extend diagonally across the s-r plane. However, transforming the data into the midpoint-offset (m-h) domain results in a vertical alignment of the wavefronts, thereby reducing the rank of the frequency slice matrix. The midpoint-offset domain is a coordinate transformation defined as: \[ \begin{equation*} \begin{split} x_{midpoint} = \frac{1}{2} (x_{source} + x_{receiver}),\\ x_{offset} = \frac{1}{2} (x_{source} - x_{receiver}).\\ \end{split} \end{equation*} \] These observations motivate us to exploit the low-rank structure of seismic data in the midpoint-offset domain for simultaneous towed-streamer acquisition. Figures 1a and 1c show a monochromatic frequency slice (at 5 Hz) for simultaneous acquisition with periodic firing times in the source-receiver (s-r) and midpoint-offset (m-h) domains, while Figures 1b and 1d show the same for simultaneous acquisition with random firing-time delays. Note that we use the source-receiver reciprocity to convert each monochromatic frequency slice of the towed-streamer acquisition to split-spread type acquisition, which is required by our current implementation of rank-minimization based techniques.

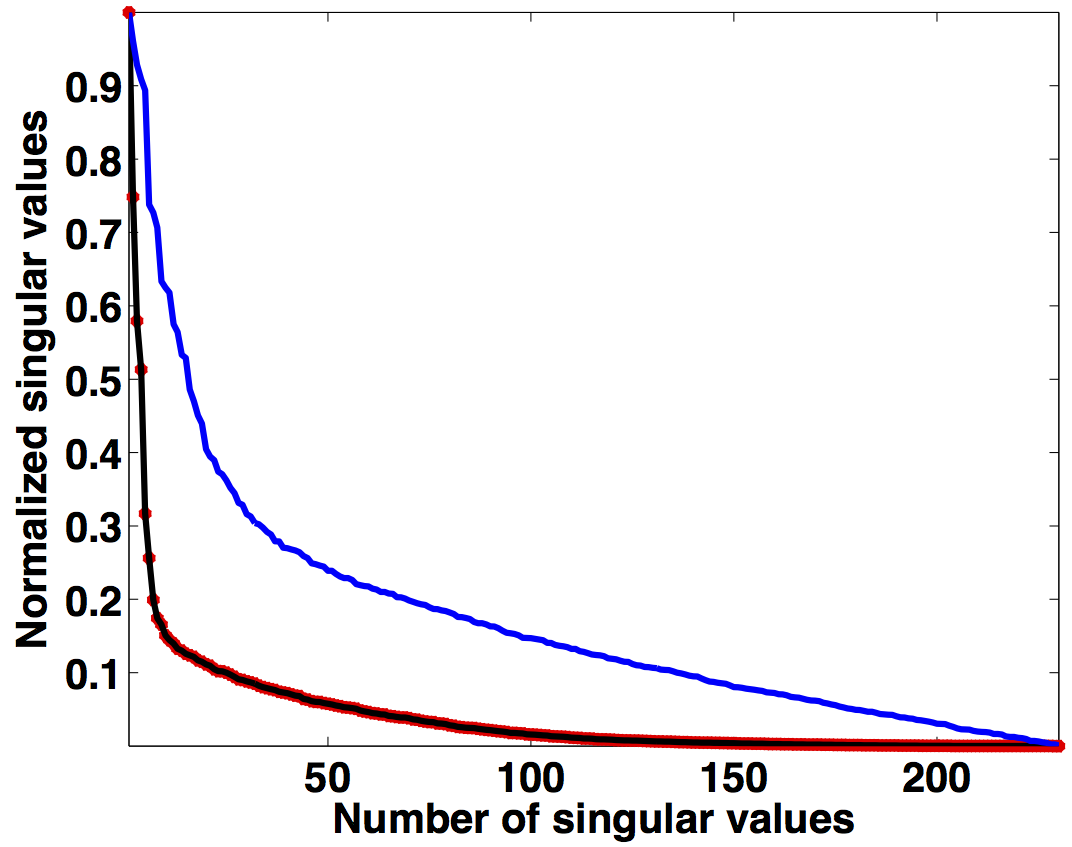
As illustrated in Figure 1, simultaneously acquired data with periodic firing times preserves continuity of the waveforms in the s-r and m-h domains, which inherently do not change the rank of blended data compared to unblended data. Introducing random time delays destroys continuity of the waveforms in the s-r and m-h domains, thus increasing the rank of the blended data matrix drastically, which is a necessary condition for rank-minimization based algorithms to work effectively. To illustrate this behaviour, we plot the decay of the singular values of a 5 Hz monochromatic frequency slice extracted from the periodically and randomized simultaneous acquisition in the s-r and m-h domains, respectively in Figure 2a. Note that uniformly random firing-time delays do not noticeably change the decay of the singular values in the source-receiver (s-r) domain, as expected, but significantly slow down the decay rate in the m-h domain.

Similar trends are observed for a monochromatic frequency slice at 40 Hz in Figure 2b. Following the same analogy, Figures 2c and 2d show how randomization in acquisition destroys the sparse structure of seismic data in the source-channel (or source-offset) domain—i.e., slow decay of the curvelet coefficients, hence, favouring recovery via sparsity-promotion in this domain. Similarly, for simultaneous long offset acquisition, we exploit the low-rank structure of seismic data in the m-h domain, and the sparse structure in the source-channel domain.

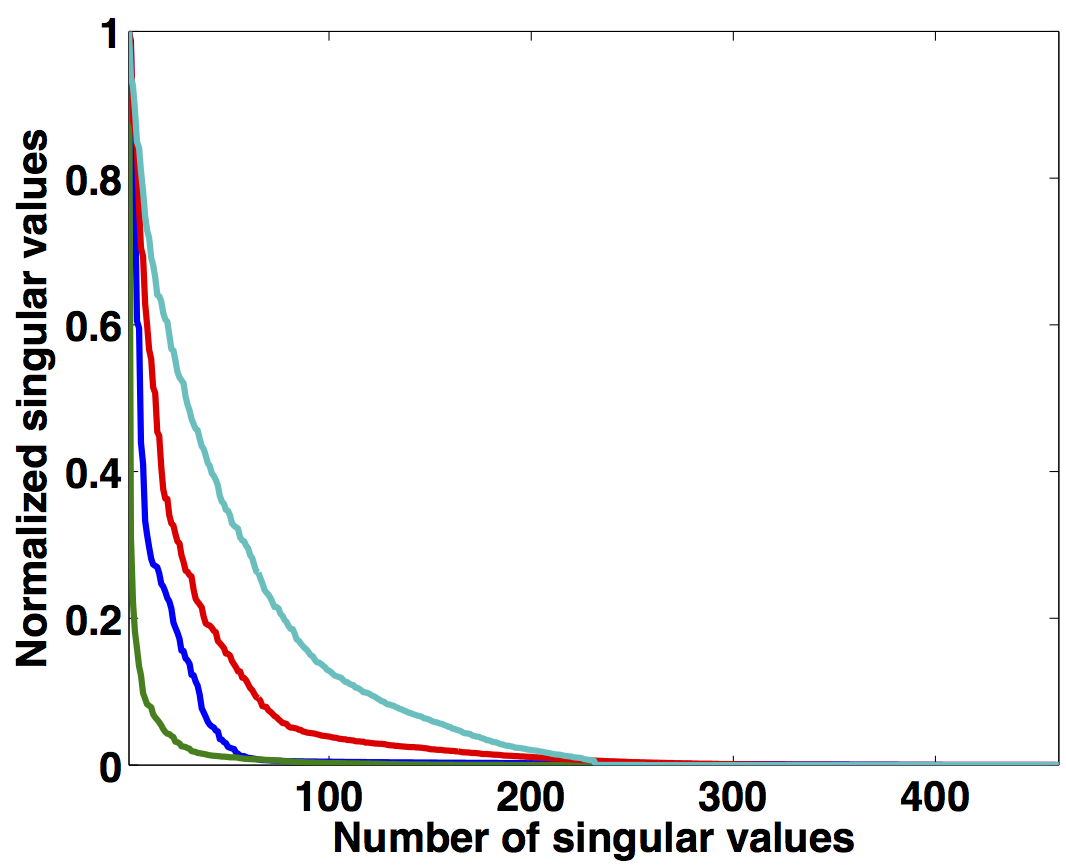
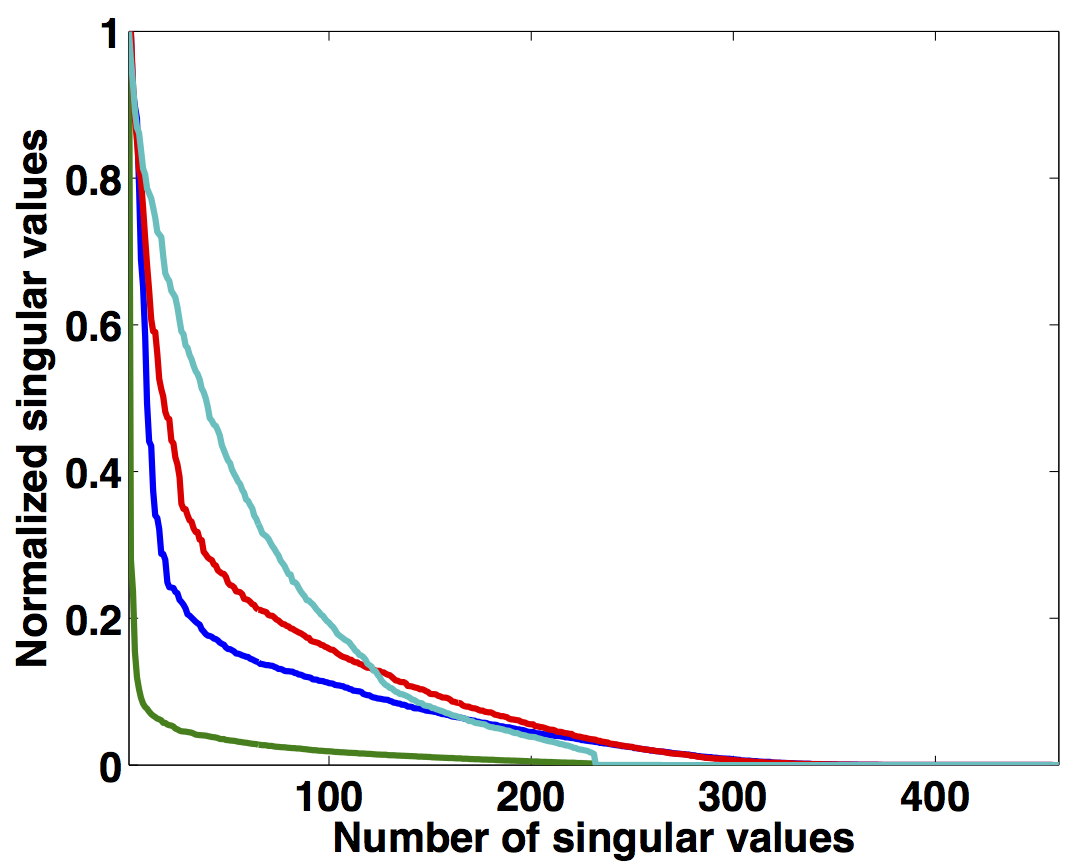
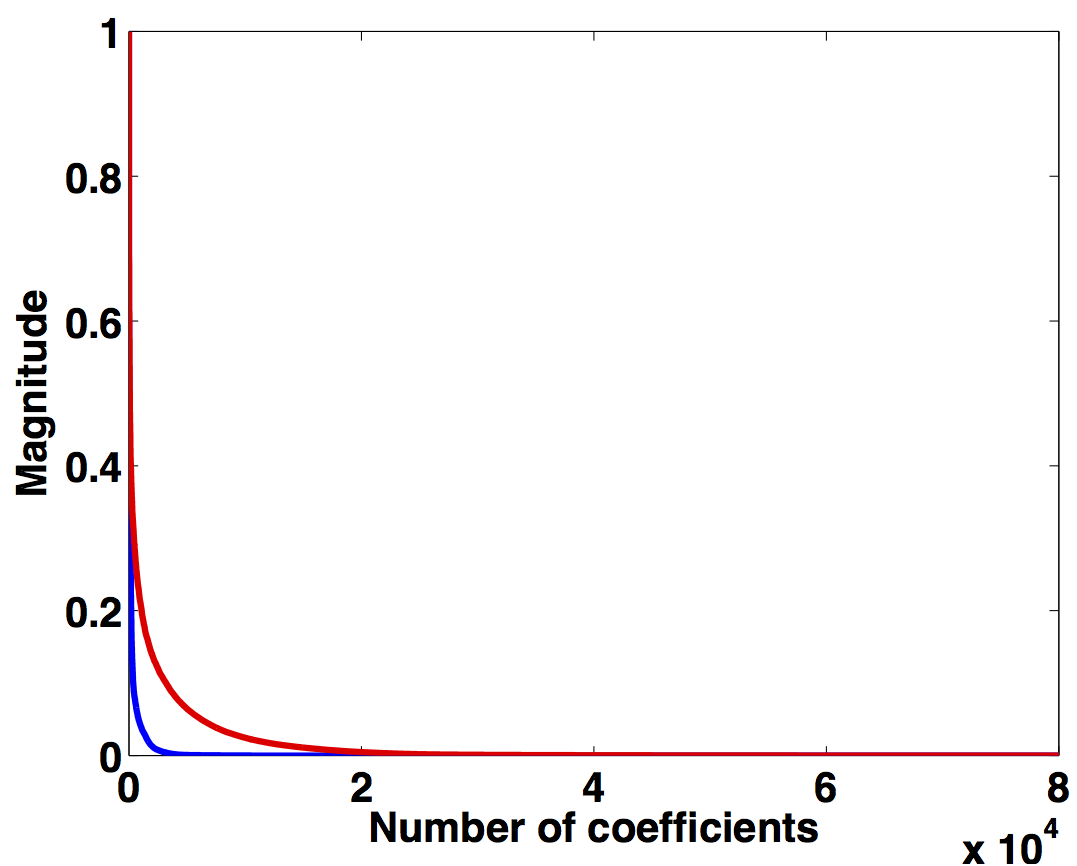
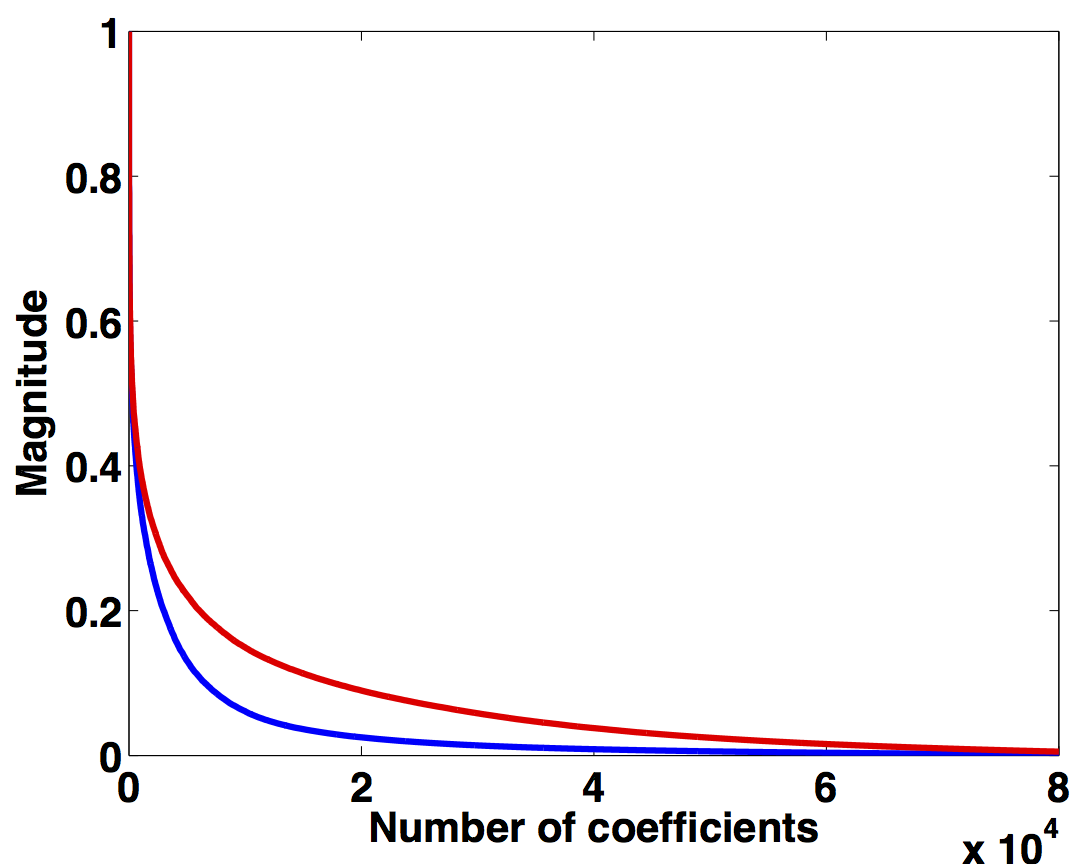
Seismic frequency slices exhibit low-rank structure in the m-h domain at low frequencies, but the same is not true for data at high frequencies. This is because in the low-frequency slices, the vertical alignment of the wavefronts can be accurately approximated by a low-rank representation. On the other hand, high-frequency slices include a variety of wave oscillations that increase the rank, even though the energy remains focused around the diagonal (Kumar et al., 2013). To illustrate this phenomenon, we plot a monochromatic frequency slice at 40 Hz in the s-r domain and the m-h domain for over/under acquisition in Figure 3. When analyzing the decay of the singular values for high-frequency slices in the s-r domain and the m-h domain (Figure 2b), we observe that the singular value decay is slower for the high-frequency slice than for the low-frequency slice. Therefore, rank-minimization in the high-frequency range requires extended formulations that incorporate the low-rank structure.

To exploit the low-rank structure of high-frequency data, we rely on the Hierarchical Semi-Separable matrix representation (HSS) method proposed by Chandrasekaran et al. (2006) to represent frequency slices. The key idea in the HSS representation is that certain full-rank matrices, e.g., matrices that are diagonally dominant with energy decaying along the off-diagonals, can be represented by a collection of low-rank sub-matrices. Kumar et al. (2013) showed the possibility of finding accurate low-rank approximations of sub-matrices of the high-frequency slices by partitioning the data into the HSS structure for missing-trace interpolation. Jumah and Herrmann (2014) showed that HSS representations can be used to reduce the storage and computational cost for the estimation of primaries by sparse inversions. They combined the HSS representation with the randomized SVD proposed by Halko et al. (2011b) to accelerate matrix-vector multiplications that are required for sparse inversion.

Hierarchical Semi-Separable matrix representation (HSS)

The HSS structure first partitions a matrix into diagonal and off-diagonal sub-matrices. The same partitioning structure is then applied recursively to the diagonal sub-matrices only. To illustrate the HSS partitioning, we consider a 2-D monochromatic high-frequency data matrix at 40 Hz in the s-r domain. We show the first-level of partitioning in Figure 4a and the second-level partitioning in Figure 4b in their corresponding source-receiver domains. Figures 5a and 5b display the first-level off-diagonal sub-blocks, Figure 5c is the diagonal sub-block, and the corresponding decay of the singular values is displayed in Figure 6. We can clearly see that the off-diagonal sub-matrices have low-rank structure, while the diagonal sub-matrices have higher rank. Further partitioning of the diagonal sub-blocks (Figure 4b) allows us to find better low-rank approximations. The same argument holds for the simultaneous long offset acquisition. Therefore, for low-variability acquisition scenarios, each frequency slice is first partitioned using HSS and then deblended in its respective m-h domain, as showed for missing-trace interpolation by Kumar et al. (2013).

One of the limitations of matrix completion type approaches for large-scale seismic data is the nuclear-norm projection, which inherently involves the computation of singular value decompositions (SVD). Aravkin et al. (2014) showed that the computation of SVD is prohibitively expensive for large-scale data such as seismic, therefore, we propose a matrix-factorization based approach to avoid the need for expensive computation of SVDs (see Aravkin et al., 2014 for details). In the next section, we introduce the matrix completion framework and explore its necessary extension to separate large-scale simultaneous seismic data.

Large-scale seismic data: SPG-LR framework

Let \({\mathbf{X}}_0\) be a low-rank matrix in \(\mathbb{C}^{n \times m}\) and \(\mathcal{A}\) be a linear measurement operator that maps from \(\mathbb{C}^{n\times m} \rightarrow \mathbb{C}^p\) with \(p \ll {n\times m}\). Under the assumption that the blending process increases the rank of the matrix \({\mathbf{X}}_0\), the source separation problem is to find the matrix of lowest possible rank that agrees with the above observations. The rank-minimization problem involves solving the following problem for \(\mathcal{A}\), up to a given tolerance \(\epsilon\): \[ \begin{equation*} \underset{\mathbf{X}}{\text{minimize}} \quad \text{rank}({\mathbf{X}}) \quad \text{subject to} \quad \|\mathcal{A} ({\mathbf{X}}) - {\mathbf{b}}\|_2 \leq \epsilon, \end{equation*} \] where \(\text{rank}\) is defined as the maximum number of linearly independent rows or column of a matrix, \(\mathbf{b}\) is a set of blended measurements. For simultaneous towed-streamer acquisition, we follow equation \(\ref{matrix}\) and redefine our system of equations as \[ \begin{equation*} \begin{aligned} \overbrace{ \begin{bmatrix} {{\mathbf{M}}{\mathbf{T}}_1}{\bf{\mathcal{S}}}^H & {{\mathbf{M}}{\mathbf{T}}_2}{\bf{\mathcal{S}}}^H \end{bmatrix} }^{\mathcal{A}} \overbrace{ \begin{bmatrix} {{\mathbf{X}}}_1 \\ {{\mathbf{X}}}_2 \end{bmatrix} }^{{\mathbf{X}}} = {{\mathbf{b}}} , \end{aligned} \end{equation*} \] where \(\mathcal{S}\) is the transformation operator from the s-r domain to the m-h domain. Recht et al. (2010b) showed that under certain general conditions on the operator \(\mathcal{A}\), the solution to the rank-minimization problem can be found by solving the following nuclear-norm minimization problem: \[ \begin{equation} \label{BPDNepsilon} \underset{\mathbf{X}}{\text{minimize}} \quad \|\mathbf{X}\|_* \quad \text{subject to} \quad \|\mathcal{A} ({\mathbf{X}}) - {\mathbf{b}}\|_2 \leq \epsilon, \tag{BPDN$_\epsilon$} \end{equation} \] where \(\left\| {\mathbf{X}}\right\|_* = \|\sigma\|_1\), and \(\sigma\) is a vector of singular values. Unfortunately, for large-scale data, solving the \(\ref{BPDNepsilon}\) problem is difficult since it requires repeated projections onto the set \(\left\| {\mathbf{X}}\right\|_* \le \tau\), which means repeated SVD or partial SVD computations. Therefore, in this paper, we avoid computing singular value decompositions (SVD) of the matrices and use an extension of the SPG\(\ell_1\) solver (Berg and Friedlander, 2008) developed for the \(\ref{BPDNepsilon}\) problem in (Aravkin et al., 2013). We refer to this extension as SPG-LR in the rest of the paper. The SPG-LR algorithm finds the solution to the \(\ref{BPDNepsilon}\) problem by solving a sequence of LASSO subproblems: \[ \begin{equation} \label{LASSO} \underset{\mathbf{X}}{\text{minimize}} \quad \|\mathcal{A} ({\mathbf{X}}) - {\mathbf{b}}\|_2 \quad \text{subject to} \quad ||{\mathbf{X}}||_* \leq \tau, \tag{LASSO$_\tau$} \end{equation} \] where \(\tau\) is updated by traversing the Pareto curve. Solving each LASSO subproblem requires a projection onto the nuclear-norm ball \(\left\| {\mathbf{X}}\right\|_* \leq \tau\) in every iteration by performing a singular value decomposition and then thresholding the singular values. For large-scale seismic problems, it becomes prohibitively expensive to carry out such a large number of SVDs. Instead, we adopt a recent factorization-based approach to nuclear-norm minimization (Rennie and Srebro, 2005; Lee et al., 2010; Recht and Re, 2011). The factorization approach parametrizes the matrix (\({\mathbf{X}}_1\), \({\mathbf{X}}_2\)) \(\in \mathbb{C}^{n\times m}\) as the product of two low-rank factors (\({\mathbf{L}}_1\), \({\mathbf{L}}_2\)) \(\in \mathbb{C}^{n\times k}\) and (\({\mathbf{R}}_1\), \({\mathbf{R}}_2\)) \(\in \mathbb{C}^{m\times k}\) such that, \[ \begin{equation} \label{product} \begin{split} {\mathbf{X}} = \begin{bmatrix} {{\mathbf{L}}_1{\mathbf{R}}_1^H} \\ {{\mathbf{L}}_2{\mathbf{R}}_2^H} \\ \end{bmatrix}. \end{split} \end{equation} \] Here, \(k\) represents the rank of the \({\mathbf{L}}\) and \({\mathbf{R}}\) factors. The optimization scheme can then be carried out using the factors (\({\mathbf{L}}_1, {\mathbf{L}}_2\)) and (\({\mathbf{R}}_1, {\mathbf{R}}_2\)) instead of (\({\mathbf{X}}_1, {\mathbf{X}}_2\)), thereby significantly reducing the size of the decision variable from \(2nm\) to \(2k(n+m)\) when \(k \ll m,n\). Rennie and Srebro (2005) showed that the nuclear-norm obeys the relationship: \[ \begin{equation} \label{nucInequality} \begin{split} \|{\mathbf{X}}\|_* \quad \leq \quad \frac{1}{2}\left\|\begin{bmatrix}{\mathbf{L}}_1 \\ {\mathbf{R}}_1 \end{bmatrix}\right\|_F^2 + \frac{1}{2} \left\|\begin{bmatrix}{\mathbf{L}}_2 \\ {\mathbf{R}}_2 \end{bmatrix}\right\|_F^2 \quad =: \quad \Phi({\mathbf{L}}_1,{\mathbf{R}}_1,{\mathbf{L}}_2,{\mathbf{R}}_2), \end{split} \end{equation} \] where \(\|\cdot\|_F^2\) is the Frobenius norm of the matrix—i.e., sum of the squared entires. Consequently, the LASSO subproblem can be replaced by \[ \begin{equation} \label{subproblem} \underset{{\mathbf{L}}_1,{\mathbf{R}}_1,{\mathbf{L}}_2,{\mathbf{R}}_2}{\text{minimize}} \quad \|\mathcal{A}({\mathbf{X}}) - {\mathbf{b}}\|_2 \quad \text{subject to} \quad \Phi({\mathbf{L}}_1,{\mathbf{R}}_1,{\mathbf{L}}_2,{\mathbf{R}}_2) \leq \tau\;, \end{equation} \] where the projection onto \(\Phi({\mathbf{L}}_1,{\mathbf{R}}_1,{\mathbf{L}}_2,{\mathbf{R}}_2) \leq \tau\) is easily achieved by multiplying each factor (\({\mathbf{L}}_1, {\mathbf{L}}_2\)) and (\({\mathbf{R}}_1, {\mathbf{R}}_2\)) by the scalar \(\sqrt{2\tau/\Phi({\mathbf{L}}_1,{\mathbf{R}}_1,{\mathbf{L}}_2,{\mathbf{R}}_2)}\). Equation \(\ref{nucInequality}\), for each HSS sub-matrix in the m-h domain, guarantees that \(\|{\mathbf{X}}\|_* \leq \tau\) for any solution of \(\ref{subproblem}\). Once the optimization problem is solved, each sub-matrix in the the m-h domain is transformed back into the s-r domain, where we concatenate all the sub-matrices to get the deblended monochromatic frequency data matrices. One of the advantages of the HSS representation is that it works with recursive partitioning of a matrix and sub-matrices can be solved in parallel, speeding up the optimization formulation.

Experiments

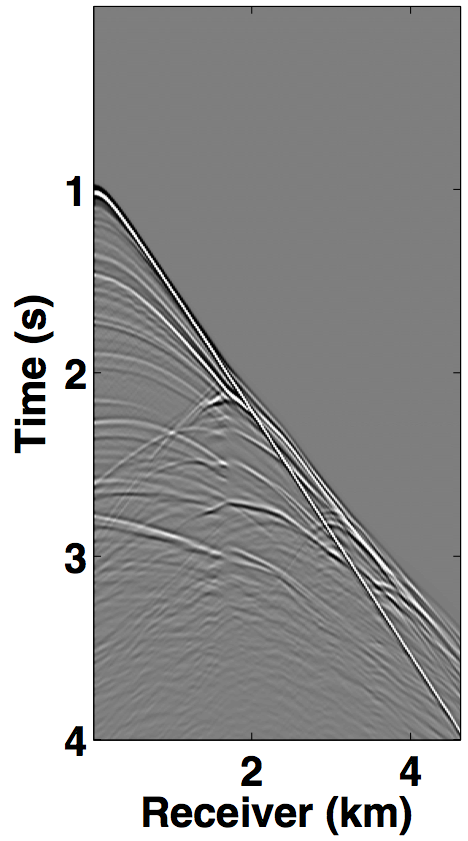
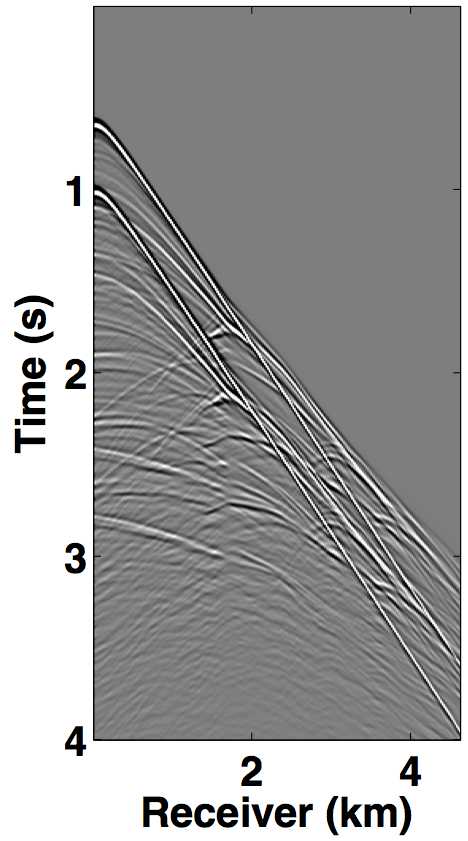
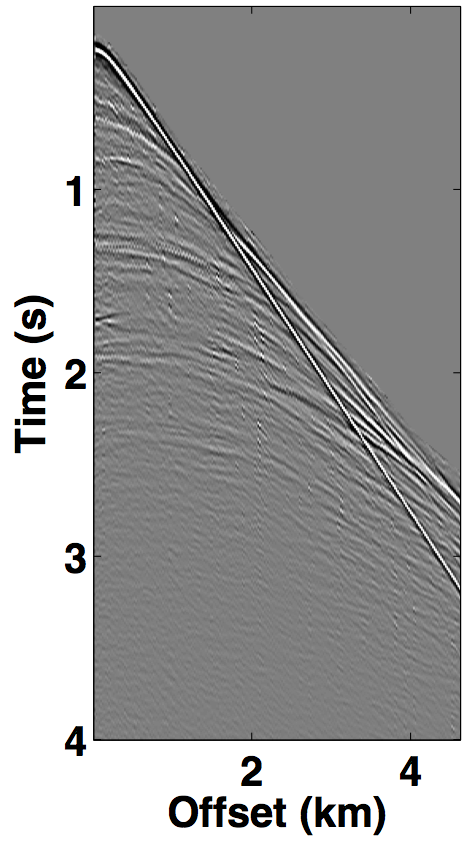
We perform source separation for two simultaneous towed-streamer acquisition scenarios—over/under and simultaneous long offset, by generating synthetic datasets on complex geological models using the IWAVE (Symes et al., 2011) time-stepping acoustic simulation software. The over/under acquisition is simulated on the Marmousi model (Bourgeois et al., 1991), which represents a complex-layer model with steeply dipping reflectors that make the data challenging. With a source (and receiver) sampling of 20.0 m, one dataset is generated with a source-depth of 8.0 m (Figure 7a), while the other dataset has the source at 12.0 m depth (Figure 7b), resulting in 231 sources and 231 receivers. The temporal length of each dataset is 4.0 s with a sampling interval of 0.004 s.

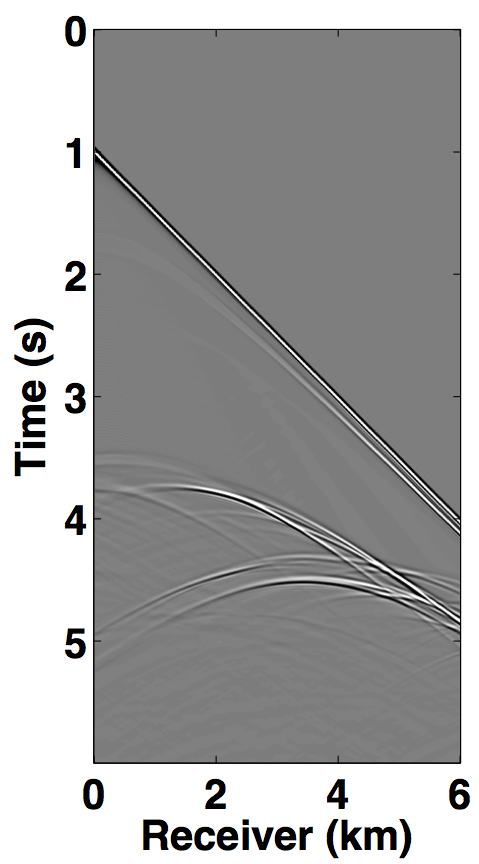
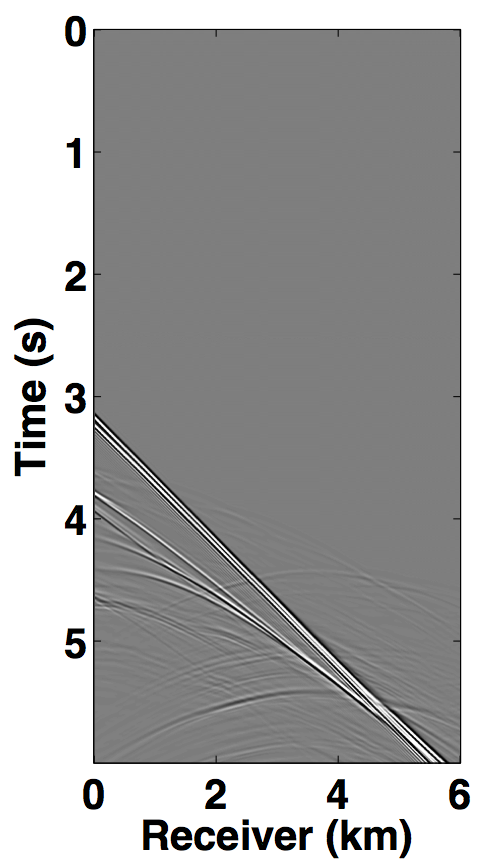
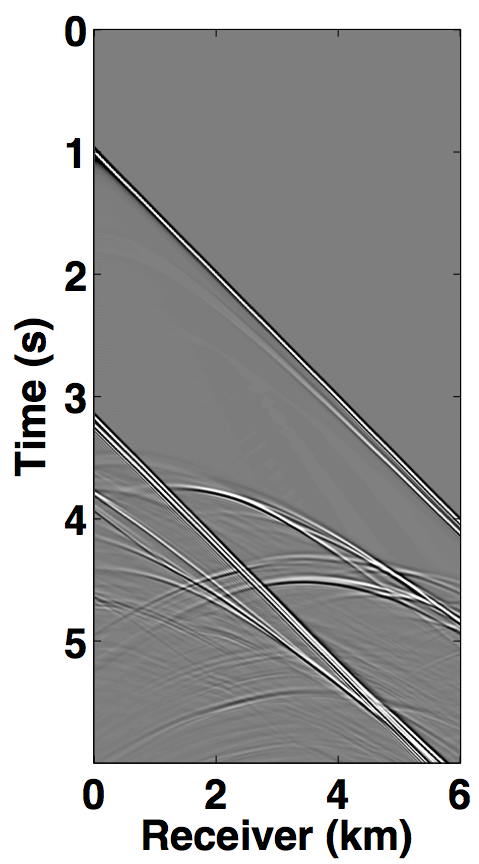
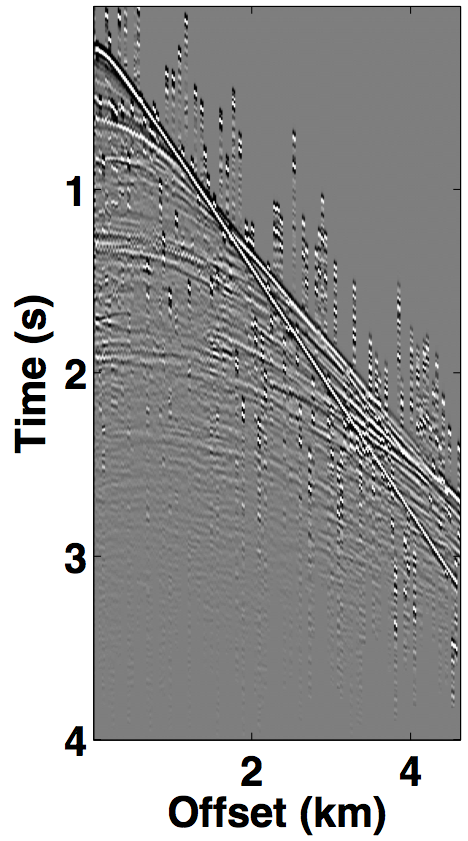
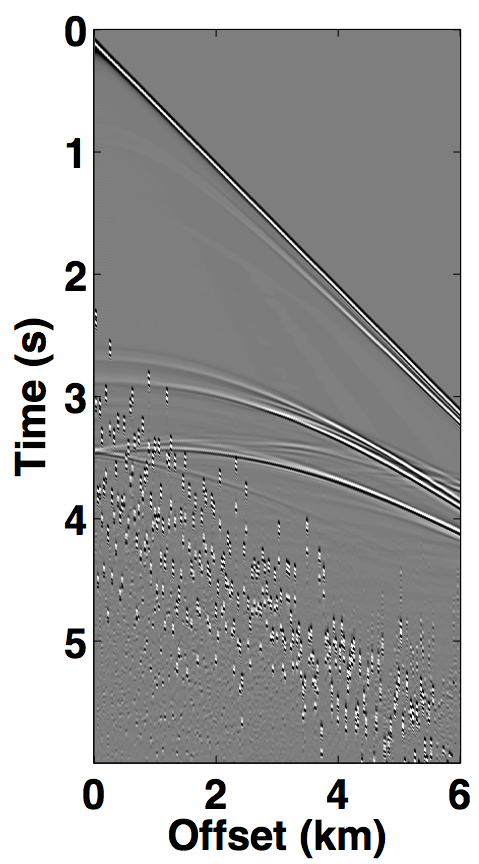
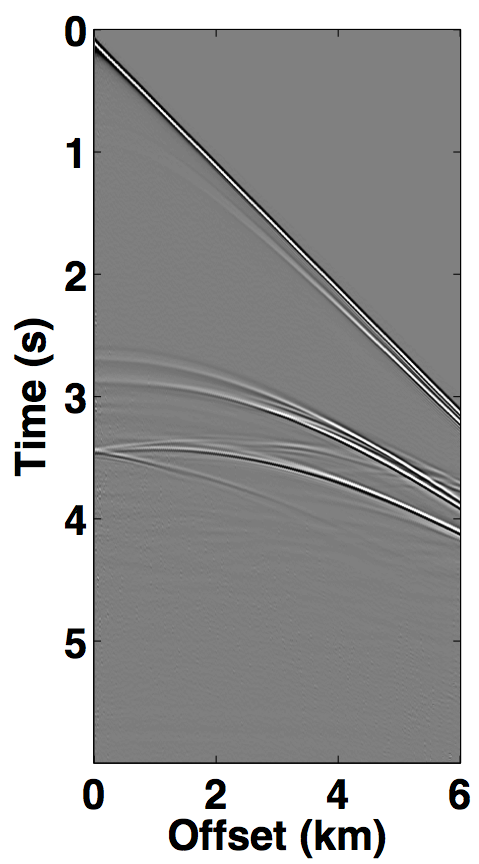
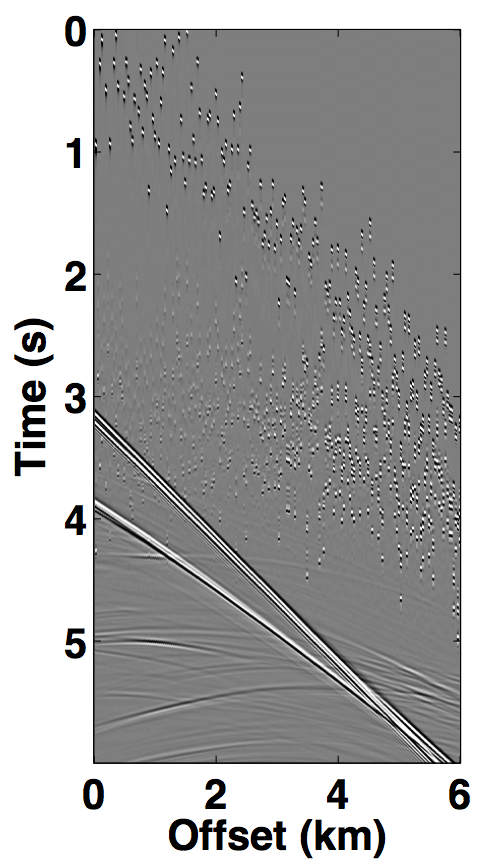
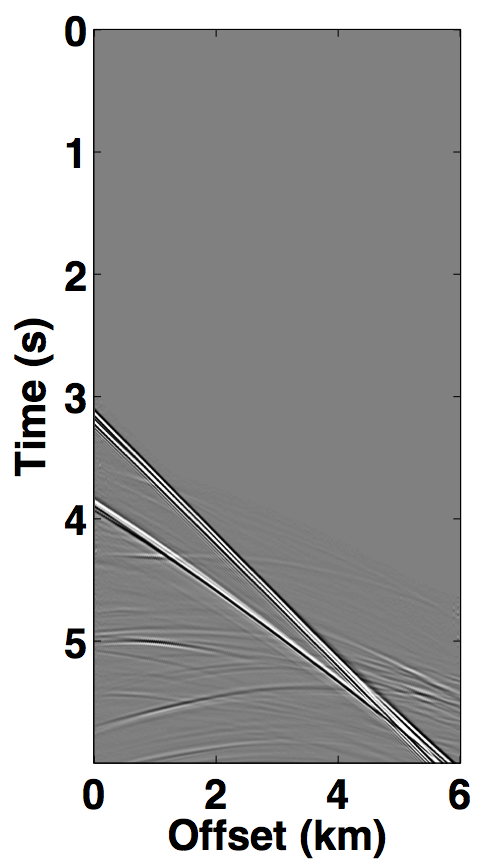
The simultaneous long offset acquisition is simulated on the BP salt model (Billette and Brandsberg-Dahl, 2004), where the presence of salt-bodies make the data challenging. The two source vessels are 6 km apart and the streamer length is 6 km. Both the datasets (for source 1 and source 2) contain 361 sources and 361 receivers with a spatial interval of 12.5 m, where the source and receiver depth is 6.25 m. The temporal length of each dataset is 6.0 s with a sampling interval of 0.006 s. A single shot gather from each dataset is shown in Figures 8a and 8b. The two datasets in both the acquisition scenarios are (simply) summed for simultaneous acquisition with periodic firing times, while uniformly random time delays between 0-1 second are applied to each source for the randomized simultaneous acquisition. The corresponding randomized blended shot gathers are shown in Figures 7c and 8c.

For deblending via rank-minimization, second-level of HSS partitioning, on each frequency slice in the s-r domain, was sufficient for successful recovery in both the acquisition scenarios. After transforming each sub-block into the m-h domain, deblending is then performed by solving the nuclear-norm minimization formulation (\(\ref{BPDNepsilon}\)) on each sub-block, using 250 iterations of SPG-LR. In order to choose an appropriate rank value, we first perform deblending for frequency slices at 2 Hz and 50 Hz. For the over/under acquisition, the best rank value is 10 and 40 for each slice, respectively. For simultaneous long offset acquisition, the best rank value is 10 and 60, respectively. Hence, we adjust the rank linearly within these ranges when moving from low to high frequencies, for each acquisition scenario. For deblending via sparsity-promotion, we use the \(\ref{eq:BPDN}\) formulation to minimize the \({\ell}_1\) norm (instead of the nuclear-norm) where the transformation operator \(\mathcal{S}\) is the 2-D curvelet operator. Here, we run 250 iterations of SPG\(\ell_1\).

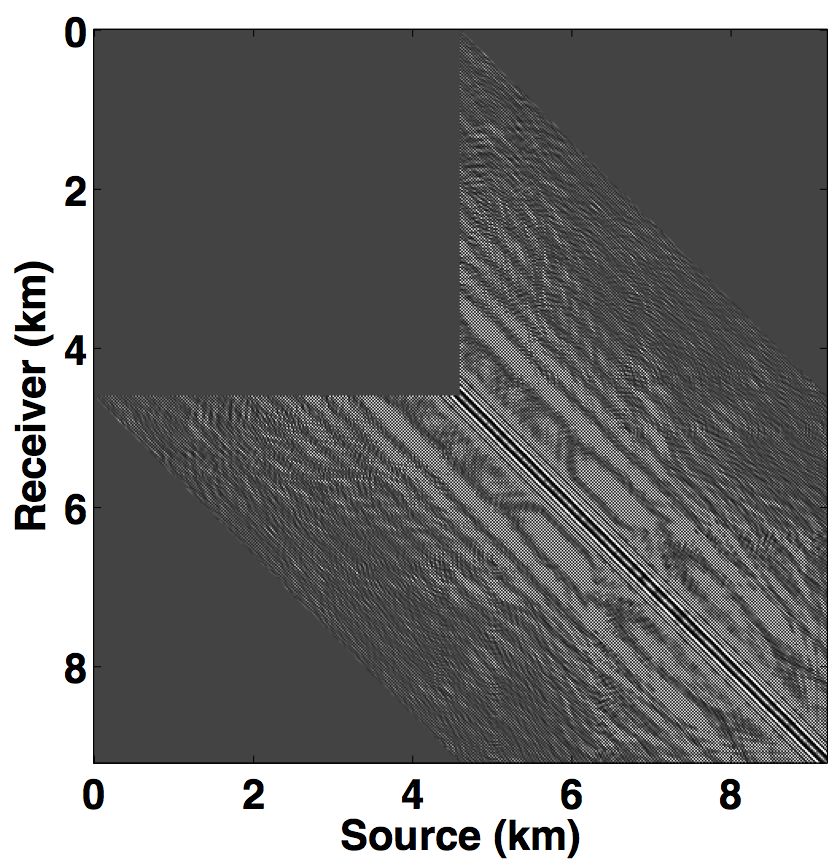
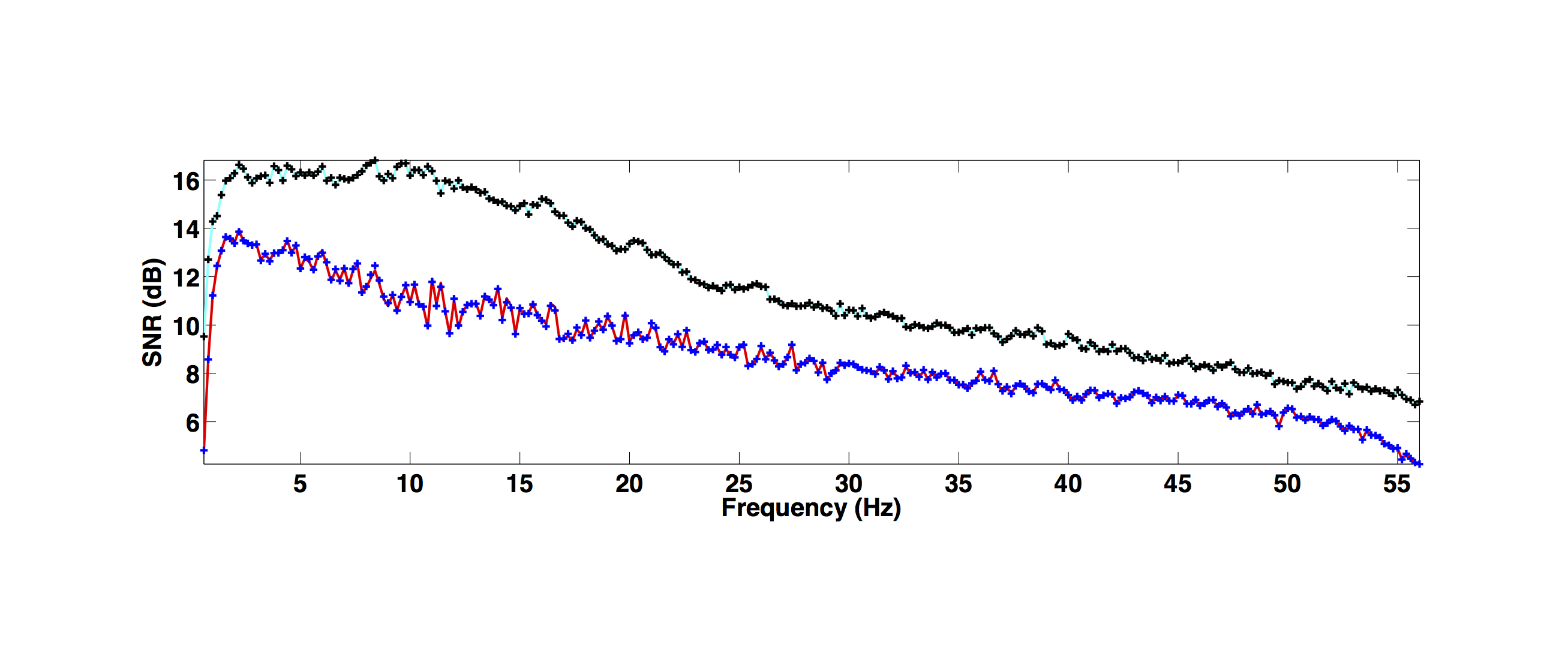
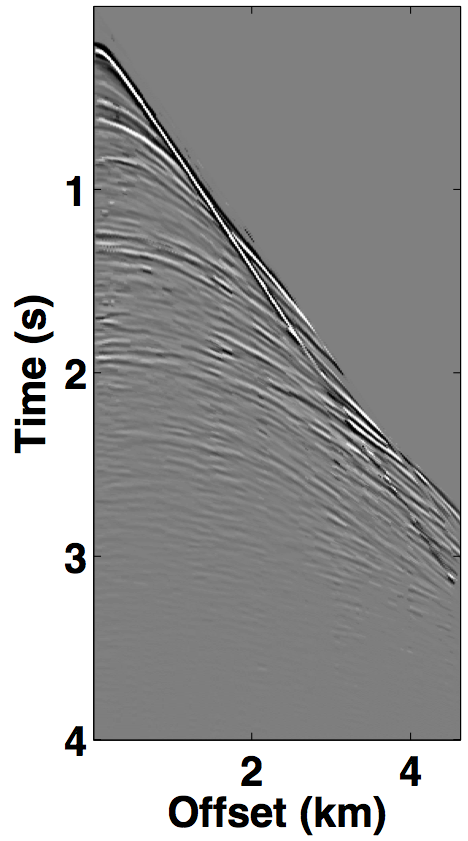
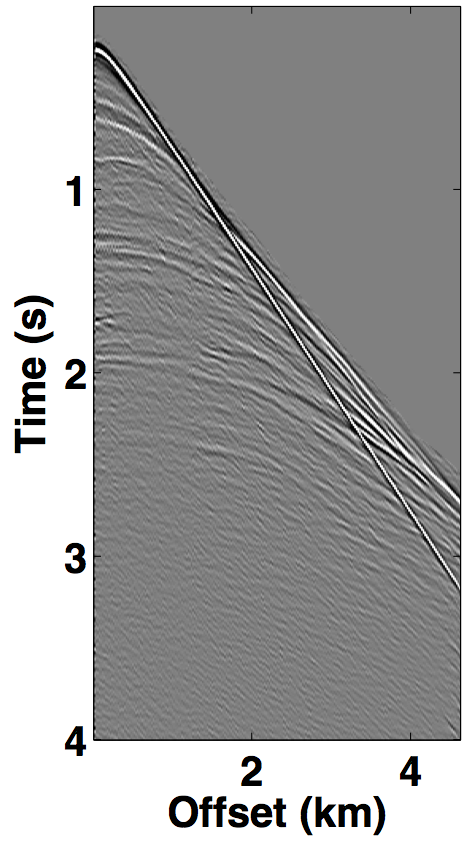
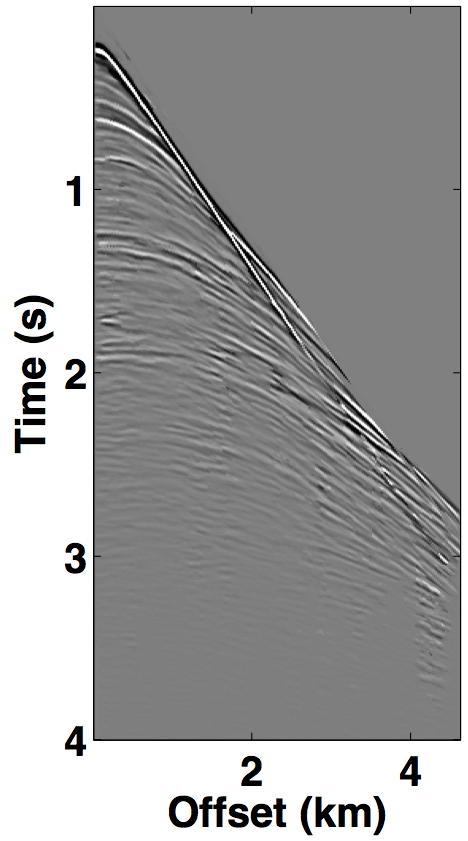
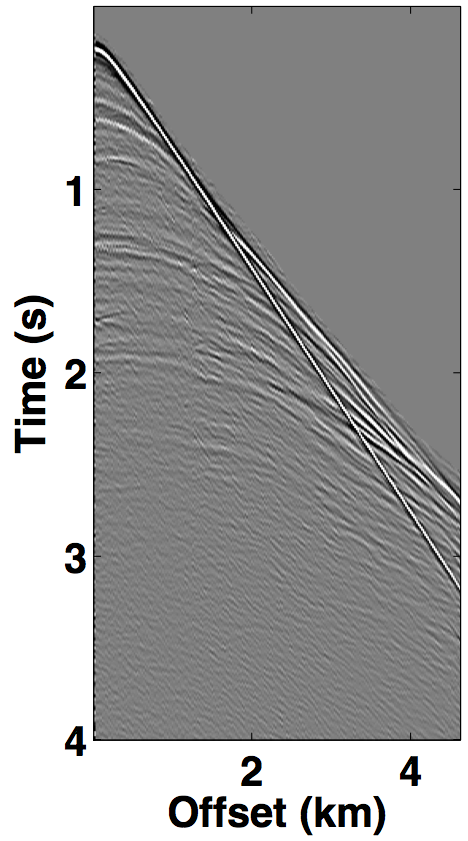
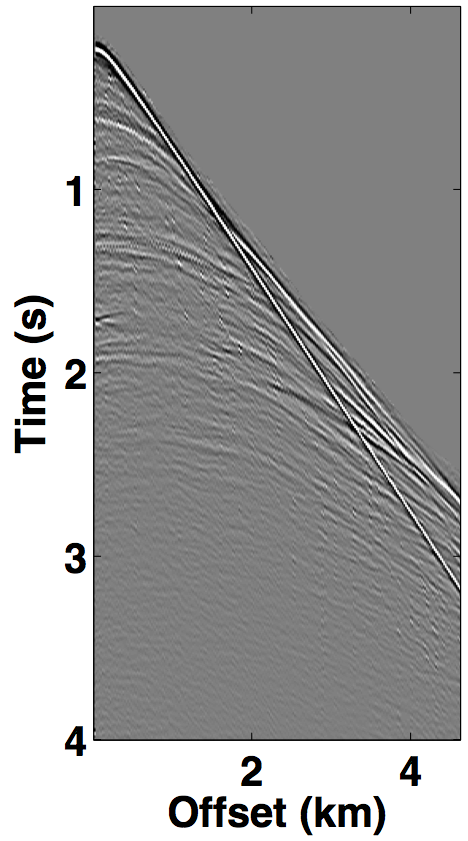
For the over/under acquisition scenario, Figures 9a and 9c show the deblended shot gathers via rank-minimization, and Figures 9b and 9d show the deblended shot gathers via sparsity-promotion, respectively. The corresponding deblended shot gathers for the simultaneous long offset acquisition scenario are shown in Figure 10. As illustrated by the results, both the CS-based approaches of rank-minimization and sparsity-promotion are able to deblend the data for the low-variability acquisition scenarios fairly well. For over/under acquisition, recovery quality of the separated sources is similar with an average signal-to-noise ratio (SNR) of 15.7 dB. For simultaneous long offset acquisition, however, the average SNRs for separation via sparsity-promotion is slightly better than rank-minimization, but recoveries from both these techniques are better than the recoveries from the over/under acquisition scenario. A possible explanation for this improvement is the long offset distance that increases randomization in the simultaneous acquisition, which is a more favourable scenario for recovery by CS-based approaches. The computational time and memory usage for sparsity-based techniques, however, is greater than the rank-minimization based techniques, as represented in Table 1. Figure 11 demonstrates the advantage of the HSS partitioning, where the SNRs of the deblended data are significantly improved.

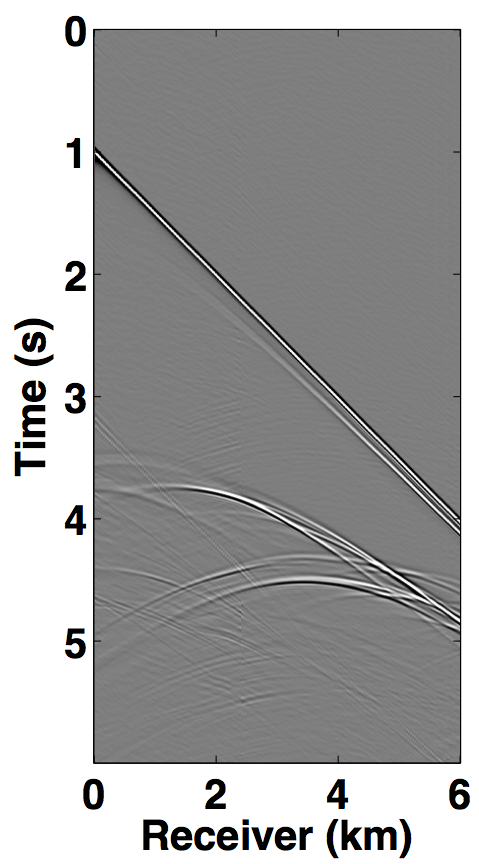
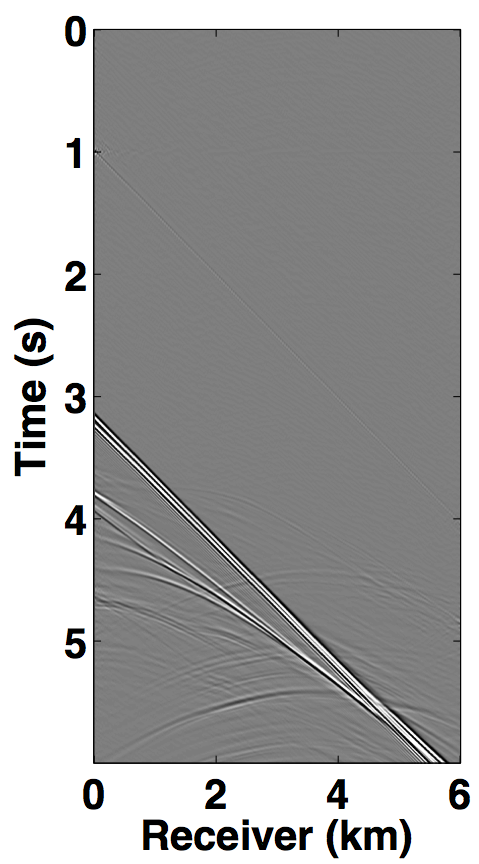
We also compare the performance of our CS-based deblending techniques with deblending using the NMO-based median filtering technique proposed by Y. Chen et al. (2014), where we work on a common-midpoint gather from each acquisition scenario. For the over/under acquisition, Figures 12a and 12e show the blended common-midpoint gathers and deblending using the median filtering technique is shown in Figures 12b and 12f. The corresponding deblended common-midpoint gathers from the two CS-based techniques are shown in Figures 12(c,d,g,h). We observe that recoveries via the proposed CS-based approaches are comparable to the recovery from the median filtering technique. Similarly, Figure 13 shows the results for the simultaneous long offset acquisition simulated on the BP salt model. Here, the CS-based techniques result in slightly improved recoveries. Although, the median filtering method is effective, however, it may suffer if applied to data with large offsets since NMO corrections result in stretching of the data.

		Marmousi model			BP salt model
	time	memory	SNR	time	memory	SNR
Sparsity	62	7.0	15.7	183	12.0	30.8, 25.0
Rank	5	2.8	15.7	19	6.0	27.0, 20.0

Discussion

The above experiments demonstrate the successful implementation of the proposed CS-based approaches of rank-minimization and sparsity-promotion for source separation in the low-variability, simultaneous towed-streamer acquisitions. The recovery is comparable for both approaches, however, separation via rank-minimization is significantly faster and memory efficient. This is further enhanced by incorporating the HSS partitioning since it allows the exploitation of the low-rank structure in the high-frequency regime, and renders its extension to large-scale data feasible.

The success of CS hinges on randomization of the acquisition. Although, the low degree of randomization (e.g., \(\leq\) 1 second) in simultaneous towed-streamer acquisitions seems favourable for source separation via CS-based techniques, however, high-variability in the firing times enhances the recovery quality of separated seismic data volumes, as shown in Wason and Herrmann (2013a); Wason and Herrmann (2013b) for ocean-bottom cable/node acquisition with continuous recording. One of the advantages of the proposed CS-based techniques is that it does not require velocity estimation, which can be a challenge for data with complex geologies. However, the proposed techniques require accurate knowledge of the random firing times.

So far, we have not considered the case of missing traces (sources and/or receivers), however, incorporating this scenario in the current framework is straightforward. This makes the problem a joint deblending and interpolation problem. In reality, seismic data are typically irregularly sampled along spatial axes, therefore, future work includes working with non-uniform sampling grids. Finally, we envisage that our methods can, in principle, be extended to separate 3-D blended seismic data volumes.

Conclusions

We have presented two compressed sensing based methods for source separation for simultaneous towed-streamer type acquisitions, such as the over/under and the simultaneous long offset acquisition. Both the compressed sensing based approaches of rank-minimization and sparsity-promotion give comparable deblending results, however, the former approach is readily scalable to large-scale blended seismic data volumes and is computationally faster. This can be further enhanced by incorporating the HSS structure with factorization-based rank-regularized optimization formulations, along with improved recovery quality of the separated seismic data. We have combined the Pareto curve approach for optimizing \(\ref{BPDNepsilon}\) formulations with the SVD-free matrix factorization methods to solve the nuclear-norm optimization formulation, which avoids the expensive computation of the singular value decomposition (SVD), a necessary step in traditional rank-minimization based methods. We find that our proposed techniques are comparable to the commonly used NMO-based median filtering techniques.

Acknowledgments

We would like to thank the authors of IWAVE (a framework for wave simulation). We would also like to thank Aleksandr Y. Aravkin for useful discussions on the implementation of the rank-minimization framework. This work was financially supported in part by the Natural Sciences and Engineering Research Council of Canada Discovery Grant (22R81254) and the Collaborative Research and Development Grant DNOISE II (375142-08). This research was carried out as part of the SINBAD II project with support from the following organizations: BG Group, BGP, CGG, Chevron, ConocoPhillips, ION, Petrobras, PGS, Statoil, Sub Salt Solutions, Total SA, WesternGeco, and Woodside.