 |
 |
 |
 | Bayesian wavefield separation by transform-domain sparsity
promotion |  |
![[pdf]](icons/pdf.png) |
Next: Bayesian signal separation
Up: Theory
Previous: Theory
The forward model
The primary-multiple separation problem is cast into a probabilistic
framework where the recorded total data vector
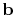 ,
,
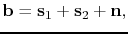 |
(1) |
is assumed to consist of a superposition of primaries,
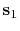 ,
multiples,
,
multiples,
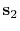 , and white Gaussian noise
, and white Gaussian noise
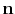 , each
component of which is
, each
component of which is
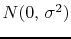 --i.e., zero-mean Gaussian with
standard deviation
--i.e., zero-mean Gaussian with
standard deviation 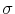 . We denote by
. We denote by
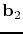 the vector
that consists of the SRME-predicted multiples. As the SRME predictions
contain errors, we assume
the vector
that consists of the SRME-predicted multiples. As the SRME predictions
contain errors, we assume
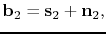 |
(2) |
where
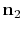 , the error in the predicted multiples is also
assumed white Gaussian; each component of
, the error in the predicted multiples is also
assumed white Gaussian; each component of
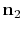 is
is
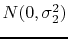 . Moreover we assume that
. Moreover we assume that
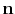 and
and
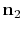 are independent.
are independent.
Following earlier work (Herrmann et al., 2007a), we write the two unknown
signal components as a superposition of curvelets--i.e.,
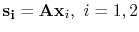 , where
, where
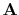 is the curvelet-synthesis matrix (Candes et al., 2006), and obtain
the system of equations
is the curvelet-synthesis matrix (Candes et al., 2006), and obtain
the system of equations
![\begin{displaymath}\begin{array}[l]{ccccc} \mathbf{b}_1&=& \tensor{A}\mathbf{x}_...
...thbf{b}_2&=& \tensor{A}\mathbf{x}_2 + \mathbf{n}_2. \end{array}\end{displaymath}](img36.png) |
(3) |
Here,
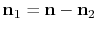 . Moreover, the unknown
curvelet coefficients for the primaries,
. Moreover, the unknown
curvelet coefficients for the primaries,
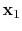 , and
multiples,
, and
multiples,
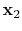 , are related to the SRME-predicted
primaries,
, are related to the SRME-predicted
primaries,
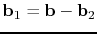 , and SRME-predicted
multiples,
, and SRME-predicted
multiples,
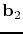 . With this formulation, we are in a
position to exploit the sparsity of the curvelet coefficient vectors
. With this formulation, we are in a
position to exploit the sparsity of the curvelet coefficient vectors
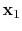 and
and
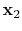 for separating the two signal
components.
for separating the two signal
components.
Remark: Note that our assumption that
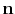 in
Equation 1 is white Gaussian noise is consistent with the
assumptions underlying the matched filter used in the SRME-multiple
prediction, see (Verschuur et al., 1992). Furthermore, our formulation
can be extended to the case where both noise contributions
in
Equation 1 is white Gaussian noise is consistent with the
assumptions underlying the matched filter used in the SRME-multiple
prediction, see (Verschuur et al., 1992). Furthermore, our formulation
can be extended to the case where both noise contributions
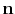 and
and
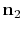 are colored Gaussian as long as the
corresponding covariance matrices are known. In the absence of an
accurate probabilistic model for the prior distribution of the error
in the predicted multiples, we make the simplifying assumption that
this error is Gaussian. As we will show in the next section, this
assumption leads to an optimization problem with a
are colored Gaussian as long as the
corresponding covariance matrices are known. In the absence of an
accurate probabilistic model for the prior distribution of the error
in the predicted multiples, we make the simplifying assumption that
this error is Gaussian. As we will show in the next section, this
assumption leads to an optimization problem with a 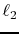 -norm
penalty for the error. In this way, we merely assign a cost function
that penalizes the
-norm
penalty for the error. In this way, we merely assign a cost function
that penalizes the 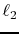 misfit between the predicted multiples
and the estimates produced by our algorithm. In addition, the
fidelity of the predicted multiples can be incorporated by choosing
the parameters in this optimization procedure appropriately.
misfit between the predicted multiples
and the estimates produced by our algorithm. In addition, the
fidelity of the predicted multiples can be incorporated by choosing
the parameters in this optimization procedure appropriately.
 |
 |
 |
 | Bayesian wavefield separation by transform-domain sparsity
promotion |  |
![[pdf]](icons/pdf.png) |
Next: Bayesian signal separation
Up: Theory
Previous: Theory
2008-03-13
![]() , where
, where
![]() is the curvelet-synthesis matrix (Candes et al., 2006), and obtain
the system of equations
is the curvelet-synthesis matrix (Candes et al., 2006), and obtain
the system of equations
![]() in
Equation 1 is white Gaussian noise is consistent with the
assumptions underlying the matched filter used in the SRME-multiple
prediction, see (Verschuur et al., 1992). Furthermore, our formulation
can be extended to the case where both noise contributions
in
Equation 1 is white Gaussian noise is consistent with the
assumptions underlying the matched filter used in the SRME-multiple
prediction, see (Verschuur et al., 1992). Furthermore, our formulation
can be extended to the case where both noise contributions
![]() and
and
![]() are colored Gaussian as long as the
corresponding covariance matrices are known. In the absence of an
accurate probabilistic model for the prior distribution of the error
in the predicted multiples, we make the simplifying assumption that
this error is Gaussian. As we will show in the next section, this
assumption leads to an optimization problem with a
are colored Gaussian as long as the
corresponding covariance matrices are known. In the absence of an
accurate probabilistic model for the prior distribution of the error
in the predicted multiples, we make the simplifying assumption that
this error is Gaussian. As we will show in the next section, this
assumption leads to an optimization problem with a ![]() -norm
penalty for the error. In this way, we merely assign a cost function
that penalizes the
-norm
penalty for the error. In this way, we merely assign a cost function
that penalizes the ![]() misfit between the predicted multiples
and the estimates produced by our algorithm. In addition, the
fidelity of the predicted multiples can be incorporated by choosing
the parameters in this optimization procedure appropriately.
misfit between the predicted multiples
and the estimates produced by our algorithm. In addition, the
fidelity of the predicted multiples can be incorporated by choosing
the parameters in this optimization procedure appropriately.