 |
 |
 |
 | Bayesian wavefield separation by transform-domain sparsity
promotion |  |
![[pdf]](icons/pdf.png) |
Next: Theory
Up: Wang et. al.: Curvelet-based
Previous: Wang et. al.: Curvelet-based
Introduction
Successful separation of coherent signal components constitutes an
important step in the seismic processing flow. Coherent noise
separation, such as primary-multiple separation as part of
Surface-Related Multiple Elimination (SRME)
(Verschuur et al., 1992; Weglein et al., 1997; Fokkema and van den Berg, 1993; Berkhout and Verschuur, 1997) or
interferometric ground-roll removal (Dong and Schuster, 2006), typically
involves two stages: a noise-prediction stage and a primary-reflection
noise separation stage. During the second stage, measures need to be
taken to compensate for moderate kinematic and dynamic errors in the
predictions of the noise components (see
e.g. Verschuur et al., 1992; Ikelle et al., 1997). For instance, 3-D complexity in the
Earth produces these types of errors during SRME
(Verschuur, 2006; Verschuur et al., 1992; Ikelle et al., 1997; Ross et al., 1999; Dragoset and Jericevic, 1998),
while multiple (van Borselen et al., 2004; Moore and Dragoset, 2004; van Dedem and Berkhout, 2005; Lin et al., 2004) and
interferometric ground-roll predictions (Dong and Schuster, 2006) become
unreliable for incomplete data acquisitions. As a result, separation
methods based on conventional (windowed) convolutional matched
filtering may not compensate adequately for these errors, rendering
noise removal ineffective.
Our main concern in this letter is the construction of an iterative
separation algorithm that is stable with respect to moderate errors in
the noise predictions. The traditional ``separation by subtraction
after matching'' approach yields predictions of signal components with
residual amplitude, timing, dip, phase, and wavelet errors. The
separation obtained via such methods can be
improved via an additional curvelet-domain nonlinear matching
procedure that can handle significant amplitude errors provided they
vary smoothly as a function of the location and dips of the noise
predictions (Herrmann et al., 2007b). Assuming that the resulting
predictions (possibly after this additional matched filtering stage)
have moderate residual errors, the algorithm proposed in this paper
complements such 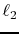 -matched-filtering techniques where noise in
the total data and errors in the noise predictions lead to residual
noise energy, high-frequency clutter, and deterioration of primary
energy (Herrmann et al., 2007a; Abma et al., 1005; Chen et al., 2004). In particular, our
algorithm takes the predictions obtained using the traditional methods
as input, and produces improved estimates of the primaries and
multiples. (For simplicity, we will refer to such predictions as the
``SRME-predictions'' although our algorithm is generic and the
predictions could be obtained using any method appropriate for the
type of wavefield-separation problem.) This is achieved by exploiting
the wavefront detection and hence separation capability of curvelets
(Herrmann et al., 2007a,2008) while offering additional
control over the energy mismatch between the SRME-predicted noise
components (the input) and the estimated signal components (the
output). Previous separation algorithms based on curvelet-domain
sparsity lack this type of control
(Herrmann et al., 2007a,2008). This letter builds
explicitly on more general results on transform-based signal
separation that will be reported
elsewhere.
-matched-filtering techniques where noise in
the total data and errors in the noise predictions lead to residual
noise energy, high-frequency clutter, and deterioration of primary
energy (Herrmann et al., 2007a; Abma et al., 1005; Chen et al., 2004). In particular, our
algorithm takes the predictions obtained using the traditional methods
as input, and produces improved estimates of the primaries and
multiples. (For simplicity, we will refer to such predictions as the
``SRME-predictions'' although our algorithm is generic and the
predictions could be obtained using any method appropriate for the
type of wavefield-separation problem.) This is achieved by exploiting
the wavefront detection and hence separation capability of curvelets
(Herrmann et al., 2007a,2008) while offering additional
control over the energy mismatch between the SRME-predicted noise
components (the input) and the estimated signal components (the
output). Previous separation algorithms based on curvelet-domain
sparsity lack this type of control
(Herrmann et al., 2007a,2008). This letter builds
explicitly on more general results on transform-based signal
separation that will be reported
elsewhere.
 |
 |
 |
 | Bayesian wavefield separation by transform-domain sparsity
promotion |  |
![[pdf]](icons/pdf.png) |
Next: Theory
Up: Wang et. al.: Curvelet-based
Previous: Wang et. al.: Curvelet-based
2008-03-13
![]() -matched-filtering techniques where noise in
the total data and errors in the noise predictions lead to residual
noise energy, high-frequency clutter, and deterioration of primary
energy (Herrmann et al., 2007a; Abma et al., 1005; Chen et al., 2004). In particular, our
algorithm takes the predictions obtained using the traditional methods
as input, and produces improved estimates of the primaries and
multiples. (For simplicity, we will refer to such predictions as the
``SRME-predictions'' although our algorithm is generic and the
predictions could be obtained using any method appropriate for the
type of wavefield-separation problem.) This is achieved by exploiting
the wavefront detection and hence separation capability of curvelets
(Herrmann et al., 2007a,2008) while offering additional
control over the energy mismatch between the SRME-predicted noise
components (the input) and the estimated signal components (the
output). Previous separation algorithms based on curvelet-domain
sparsity lack this type of control
(Herrmann et al., 2007a,2008). This letter builds
explicitly on more general results on transform-based signal
separation that will be reported
elsewhere.
-matched-filtering techniques where noise in
the total data and errors in the noise predictions lead to residual
noise energy, high-frequency clutter, and deterioration of primary
energy (Herrmann et al., 2007a; Abma et al., 1005; Chen et al., 2004). In particular, our
algorithm takes the predictions obtained using the traditional methods
as input, and produces improved estimates of the primaries and
multiples. (For simplicity, we will refer to such predictions as the
``SRME-predictions'' although our algorithm is generic and the
predictions could be obtained using any method appropriate for the
type of wavefield-separation problem.) This is achieved by exploiting
the wavefront detection and hence separation capability of curvelets
(Herrmann et al., 2007a,2008) while offering additional
control over the energy mismatch between the SRME-predicted noise
components (the input) and the estimated signal components (the
output). Previous separation algorithms based on curvelet-domain
sparsity lack this type of control
(Herrmann et al., 2007a,2008). This letter builds
explicitly on more general results on transform-based signal
separation that will be reported
elsewhere.