 |
 |
 |
 | Adaptive curvelet-domain primary-multiple separation |  |
![[pdf]](icons/pdf.png) |
Next: Our contribution:
Up: Adaptive curvelet-domain primary-multiple separation
Previous: Adaptive curvelet-domain primary-multiple separation
Surface-Related Multiple Elimination (SRME)
(Verschuur et al., 1992; Weglein et al., 1997; Fokkema and van den Berg, 1993; Berkhout and Verschuur, 1997) involves two
stages, namely multiple prediction and primary-multiple separation.
During the second stage, measures are taken to compensate for
imperfections in the multiple predictions. For SRME, predicted
multiples often include source signatures and directivity patterns
that differ from those present in the data (see
e.g. Verschuur et al., 1992; Ikelle et al., 1997). Moreover, 2D SRME produces errors in
the predicted multiples due to 3D complexity of the Earth
(Verschuur, 2006; Ross et al., 1999; Dragoset and Jericevic, 1998), while recently-developed
full 3D-SRME algorithms may suffer from imperfections related to
incomplete acquisitions (see
e.g. van Borselen et al., 2004; Moore and Dragoset, 2004; van Dedem and Verschuur, 2005; Lin et al., 2004), including erroneous
reconstructions of missing near offsets (Dragoset and Jericevic, 1998). For field
data, these factors preclude iterative SRME, resulting in amplitude
errors that vary for different multiple orders (see
e.g. Pfaffenholz et al., 2002; Verschuur and Berkhout, 1997).
In practice, the second separation stage appears particularly
challenging since adaptive 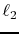 -matched-filtering techniques are
known to lead to residual multiple energy, high-frequency clutter and
deterioration of the primaries
(Herrmann et al., 2007b; Abma et al., 2005; Chen et al., 2004). By employing the curvelet
transform's ability (Candes et al., 2006; Hennenfent and Herrmann, 2006) to
detect wavefronts with conflicting dips (e.g. caustics),
Herrmann et al. (2007b,d) were able to derive a
non-adaptive (independent of the total data) separation scheme that
uses the original data and SRME-predicted multiples as input and
produces an estimate for the primaries. This threshold-based method
proved robust with respect to moderate errors (sign, phase and
timing) in the predicted multiples, and derived its success from the
sparsifying property of curvelets for data with wavefronts.
Despite recent advances in thresholding, by a Bayesian formulation
(Saab et al., 2007; Wang et al., 2007), and mitigation of the effects of missing
data (Herrmann et al., 2007a; Hennenfent and Herrmann, 2007), curvelet-domain
separation deteriorates when the predicted multiples have significant
amplitude errors. Thresholding in these cases may give rise to
inadvertent removal of primary energy or to remnant multiple energy.
-matched-filtering techniques are
known to lead to residual multiple energy, high-frequency clutter and
deterioration of the primaries
(Herrmann et al., 2007b; Abma et al., 2005; Chen et al., 2004). By employing the curvelet
transform's ability (Candes et al., 2006; Hennenfent and Herrmann, 2006) to
detect wavefronts with conflicting dips (e.g. caustics),
Herrmann et al. (2007b,d) were able to derive a
non-adaptive (independent of the total data) separation scheme that
uses the original data and SRME-predicted multiples as input and
produces an estimate for the primaries. This threshold-based method
proved robust with respect to moderate errors (sign, phase and
timing) in the predicted multiples, and derived its success from the
sparsifying property of curvelets for data with wavefronts.
Despite recent advances in thresholding, by a Bayesian formulation
(Saab et al., 2007; Wang et al., 2007), and mitigation of the effects of missing
data (Herrmann et al., 2007a; Hennenfent and Herrmann, 2007), curvelet-domain
separation deteriorates when the predicted multiples have significant
amplitude errors. Thresholding in these cases may give rise to
inadvertent removal of primary energy or to remnant multiple energy.
Subsections
 |
 |
 |
 | Adaptive curvelet-domain primary-multiple separation |  |
![[pdf]](icons/pdf.png) |
Next: Our contribution:
Up: Adaptive curvelet-domain primary-multiple separation
Previous: Adaptive curvelet-domain primary-multiple separation
2008-01-18
![]() -matched-filtering techniques are
known to lead to residual multiple energy, high-frequency clutter and
deterioration of the primaries
(Herrmann et al., 2007b; Abma et al., 2005; Chen et al., 2004). By employing the curvelet
transform's ability (Candes et al., 2006; Hennenfent and Herrmann, 2006) to
detect wavefronts with conflicting dips (e.g. caustics),
Herrmann et al. (2007b,d) were able to derive a
non-adaptive (independent of the total data) separation scheme that
uses the original data and SRME-predicted multiples as input and
produces an estimate for the primaries. This threshold-based method
proved robust with respect to moderate errors (sign, phase and
timing) in the predicted multiples, and derived its success from the
sparsifying property of curvelets for data with wavefronts.
Despite recent advances in thresholding, by a Bayesian formulation
(Saab et al., 2007; Wang et al., 2007), and mitigation of the effects of missing
data (Herrmann et al., 2007a; Hennenfent and Herrmann, 2007), curvelet-domain
separation deteriorates when the predicted multiples have significant
amplitude errors. Thresholding in these cases may give rise to
inadvertent removal of primary energy or to remnant multiple energy.
-matched-filtering techniques are
known to lead to residual multiple energy, high-frequency clutter and
deterioration of the primaries
(Herrmann et al., 2007b; Abma et al., 2005; Chen et al., 2004). By employing the curvelet
transform's ability (Candes et al., 2006; Hennenfent and Herrmann, 2006) to
detect wavefronts with conflicting dips (e.g. caustics),
Herrmann et al. (2007b,d) were able to derive a
non-adaptive (independent of the total data) separation scheme that
uses the original data and SRME-predicted multiples as input and
produces an estimate for the primaries. This threshold-based method
proved robust with respect to moderate errors (sign, phase and
timing) in the predicted multiples, and derived its success from the
sparsifying property of curvelets for data with wavefronts.
Despite recent advances in thresholding, by a Bayesian formulation
(Saab et al., 2007; Wang et al., 2007), and mitigation of the effects of missing
data (Herrmann et al., 2007a; Hennenfent and Herrmann, 2007), curvelet-domain
separation deteriorates when the predicted multiples have significant
amplitude errors. Thresholding in these cases may give rise to
inadvertent removal of primary energy or to remnant multiple energy.