Compressed sensing based land simultaneous acquisition using encoded sweeps

Abstract

Simultaneous shooting methods using encoded sweeps can enhance the productivity of land acquisition in situations where deployment of many vibrators and larger receiver spread is not possible in the field due to obstructions or permit limitations. However, the existing framework requires shooting the full sequence of encoded sweeps on each shot point to reconstruct the complete frequency bandwidth Green’s function. Although this simultaneous shooting method reduces the sweeping time vs conventional sequential shooting, the gain in efficiency is limited. To further reduce the sweeping time, we propose to acquire randomly selected subsets of the encoded sweeps sequences followed by a rank-minimization based joint source separation and spectral interpolation framework to reconstruct the full bandwidth deblended Green’s function. We demonstrate the advantages of proposed sampling and reconstruction framework using a synthetic seismic line simulated using SEAM land velocity and density model.

Introduction

Simultaneous shooting has completely changed the game of land seismic data acquisition, where sustainable productivity gains is achieved with more than 25,000 vibrators points per day. Moreover, simultaneous source methods with encoding make it possible to record seismic data with source sampling that is now as dense as receiver sampling. This has tremendous advantages especially for coherent noise removal (multiples and groundroll) and imaging. Several different approaches exist that handle simultaneous source land data including methods such as independent simultaneous shooting (ISS) (Howe et al. (2008)), randomly phase-encoded vibroseis sweeps ((???)), distance-separated simultaneous shooting (Bouska (2010)), master spread and source (MSS) ((???)) and compressed seismic imaging ((???)). All these approaches assumed that a large number of single vibrators are placed at separate shot stations covering a larger receiver spread. Even though these methods may provide high productivity rates, they cannot be used in areas where a large number of vibrators and receivers are not available or the field access is restricted due to obstructions or permit limitation.

To overcome this problem, Moldoveanu et al. (2017) proposes a phase- and frequency-encoding method, where a conventional sweep of length \(L\) and frequency bandwidth \(\Omega\) is divided into \(n\) non-overlapping segments. Each segment is of length \(\frac{L}{n}\), frequency bandwidth of \(\frac{\Omega}{n}\) and has a different phase (Figure 1). Number of segments corresponds to the number of shot points acquired simultaneously. At each shot location, the vibrators will sweep a sequence of \(n\) segments, but each sequence will have a different order of the segmented sweeps. The segments are orthogonal to each other. To recover the full bandwidth signal at each location, Moldoveanu et al. (2017) perform source separation and summed the \(n\) separated shots at each source location (Figure 1). Source separation can be performed with crosscorrelation or inversion. One benefit of phase- and frequency-encoding scheme is that it does not require a large distance between vibrators that sweep simultaneously and vibrators can be placed on consecutive source lines. A second benefit is that the sweeping time is reduced compared to the conventional shooting where a full sweep is used.

To take the phase- and frequency-encoding method a step further, we propose to adapt ideas from compressive sensing (see this for details Donoho (2006); Candes et al. (2006); F. J. Herrmann et al. (2012)) and randomly subsample the \(n\) sweep segments and only acquire \({P}\) simultaneous sources, where \(P \ll n_s\). This will further reduce the recording time by a factor of \(\frac{n_s}{P}\). To recover the full bandwidth signal as if we collected the data conventionally with broadband sequential sweep, we perform our joint source separation and spectral interpolation by utilizing the fact that underlying signal of interest exhibits low-rank structure in some transform domain. The abstract is organized as follows. First, we discuss the simultaneous shooting setup and then we talk about the random selections of sweep sequences. Next, we explain the computationally efficient rank-minimization framework to perform the joint separation and interpolation, which can handle large-scale seismic data. Finally, we demonstrate the performance of our method on a synthetic 2D seismic line simulated from a cross section of the SEG-SEAM Phase II land model ((???)).

Acquisition setup

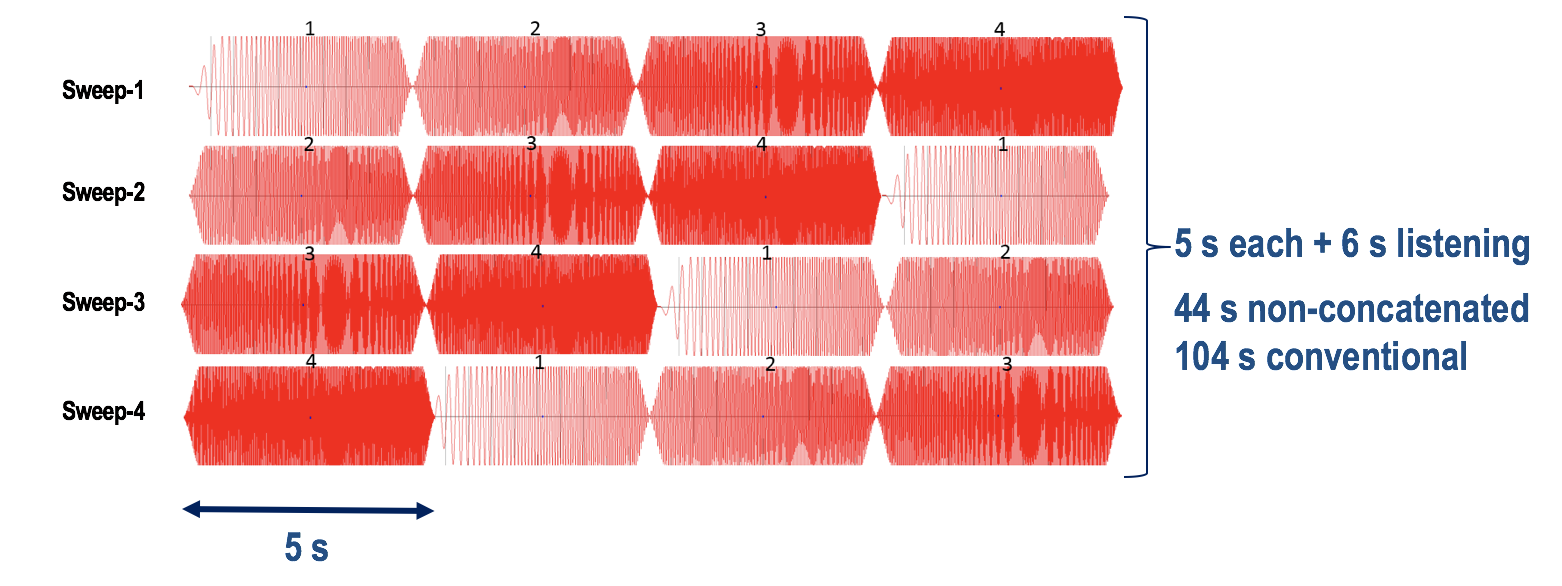
To acquire high-fidelity vibratory seismic acquisition that uses phase- and frequency-encoding scheme, we split the conventional single source sweep of length 20 s, listening time of 6 s and frequency bandwidth from 2-90 Hz into four segments. As shown in Figure 1, each segment contain a different frequency band \(\Omega\) and a different phase \(\Psi\) . The sweep length for each segment is 5 s. During the acquisition, all four vibrators simultaneously generate four different sweeps combinations (see rows in Figure 1), which result in four different simultaneous shots with different phase and frequency encoding. Since, each vibrator generates four different sweeps at each station (see the columns in Figure 1 for detail), the total sweeping and listening time to record the full frequency band at each of the four fixed stations becomes 44 s. Note that, in a conventional single sweep experiment, the total sweeping and listening time to record one source experiment is 26 s, therefore, it takes 104 s to record full bandwidth seismic signal at four source locations. This reduced sweeping time could translate in an increased acquisition efficiency by a factor of \(\approx 2\).

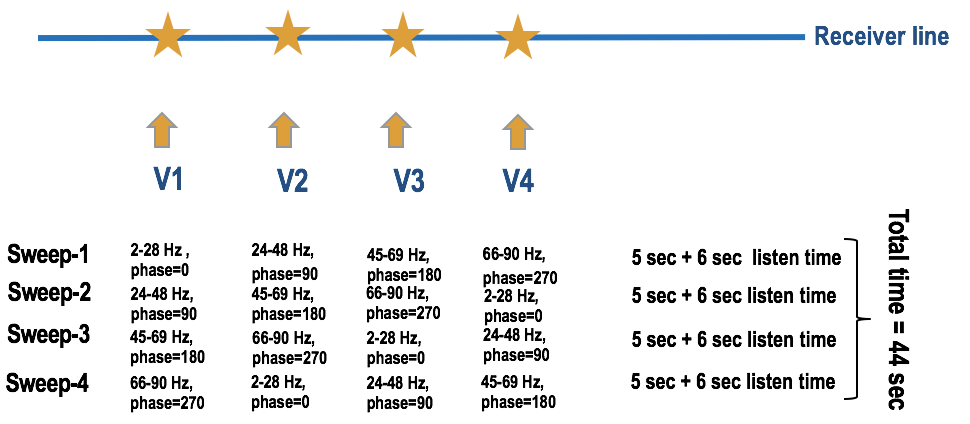
To make the above approach more practical and cost effective, we propose to acquire the randomly subsampled simultaneous sweeps sequences (rows in Figure 1) at each of the four fixed stations. Note that, without missing the sweep sequences, we can use the source separation techniques to reconstruct the full bandwidth Green’s function. Because we are randomly subsampling the sweep sequences, it will create gaps in the frequency spectrum. For that reason, we present a joint rank-minimization based source separation and spectral interpolation framework in the next section to recover the full bandwidth deblended Green’s function.

Rank-minimization

Let \(\mathbf{X}\) represents the fully sampled Green’s function in the frequency-midpoint-offset domain and \(\mathcal{A}\) represents a combined convolution, blending, and subsampling operator that maps the fully sampled full band Green’s function \(\mathbf{X}\) from the frequency-midpoint-offset domain to the observed subsampled and blended seismic data \(\mathbf{b}\) in the physical time-source-receiver domain. The dimensions of \(\mathbf{X}\) and \(\mathbf{b}\) are \(N_f \times N_m \times N_h\) and \(N_{tot} \times N_r \times N_{sub}\), respectively. Note that, \(N_f\) represents the number of frequencies, \(N_r\) represents the number of receivers, \(N_{tot}\) represents the total listening time for each simultaneous source, \(N_{sub}\) represents the number of randomly selected simultaneous source after removing a predefined number of sweep sequences, i.e., rows in Figure 1, and \(N_m, N_h\) represent the number of midpoints and offsets, respectively. The forward operator \(\mathcal{A}\) acts over all frequencies in \(\mathbf{X}\) and is composed of the product of the transformation operator \(\mathcal{S} \in \mathbb{C}^{(N_fN_mN_h) \times (N_fN_rN_s)}\), restriction operators \(\mathbf{R} \in \mathbb{C}^{(N_fN_rN_{sub}) \times (N_fN_rN_s)}\), and operator \(\mathbf{B}\), which blend the Green’s function at fixed four stations after convolving them with the corresponding sweep segments (columns in Figure 1). The Fourier transform operator \({\mathbf{F}}_t\) acts along the time axis, i.e., \(\mathcal{A} = {\mathbf{F}}_t^{-1}{\mathbf{RB}}{\mathcal{S}}^H\), where \(^H\) denotes the Hermitian transpose. The blending operator \(\mathbf{B}\) is a block diagonal matrix, i.e., \(\text{Blockdiag}_{{\mathbf{B}}_1 \cdots {\mathbf{B}}_k}\), where the total number of blocks, i.e., \(k\) depends upon the number of sources \(N_s\) in the conventional acquisition and is equal to \(\frac{N_s}{4}\). Each sub-block \({\mathbf{B}}_i, i = 1 \cdots k\) represents a \(4 \times 4\) convolution and blending matrix as shown below \[ \begin{equation} \begin{aligned} \mathbf{B}_i = \begin{pmatrix} \text{diag}(a_1) & \text{diag}(a_2) & \text{diag}(a_3) & \text{diag}(a_4) \\ \text{diag}(a_2) & \text{diag}(a_3) & \text{diag}(a_4) & \text{diag}(a_1) \\ \text{diag}(a_3) & \text{diag}(a_4) & \text{diag}(a_1) & \text{diag}(a_2) \\ \text{diag}(a_4) & \text{diag}(a_1) & \text{diag}(a_2) & \text{diag}(a_3) \end{pmatrix}. \end{aligned} \label{sweepeq} \end{equation} \] Here, \(a_1, a_2, a_3\) and \(a_4\) represent the four sweep segments converted into the frequency domain and \(\text{diag}(x)\) returns a square diagonal matrix with the elements of vector \(x\) on the main diagonal. Under the assumption that the fully sampled Green’s function \(\mathbf{X}\) exhibit a low-rank structure in some transform domain, we can perform the joint source separation and interpolation by solving the following nuclear-norm minimization problem \[ \begin{equation} \underset{\mathbf{X}}{\text{minimize}} \quad \|\mathbf{X}\|_* \quad \text{subject to} \quad \|\mathcal{A} ({\mathbf{X}}) - {\mathbf{b}}\|_2 \leq \epsilon, \label{BPDNnuc} \end{equation} \] where \(\left\| \mathbf{X}\right\|_* = \|\sigma\|_1\), and \(\sigma\) is the vector of singular values. For a seismic line, Aravkin et al. (2014) showed that seismic data exhibit low-rank structure in the midpoint-offset domain and that randomized subsampling destroys this low-rank structure in the midpoint-offset domain. Hence, in our example, the forward operator \(\mathcal{S}\) transforms the monochromatic frequency slices from the source-receiver domain to the midpoint-offset domain and its adjoint transforms the slices back to the source-receiver domain. For brevity, we exclude details of solving equation \(\ref{BPDNnuc}\) and choice of the midpoint-offset domain to exploit the low-rank structure. Interested readers are referred to Aravkin et al. (2014); Kumar et al. (2015) where the rank-revealing transform domains for 2D and 3D seismic acquisition and the implementation of a computationally efficient framework for solving the nuclear-norm minimization problem for large-scale seismic data problem are discussed in detail.

SEAM 2D Land model

To validate the rank-minimization based joint source separation and spectral interpolation approach, we used a 2D acoustic velocity and density profile derived from the 3D land model developed during SEG-SEAM Phase II, which is an industry-led consortium addressing critical land seismic challenges through advanced modeling ((???)). For this example, the velocity model was \(7\,\mathrm{km}\) deep and \(40\,\mathrm{km}\) wide sampled at \(12.5\,\mathrm{m}\) in \(\mathbf{x}\) and \(\mathbf{z}\). The synthetic fully sampled Green’s function is generated using a time-domain finite difference modeling code (Lange et al. (2017)), which contains \(720\) sources and receivers sampled at \(50\,\mathrm{m}\), respectively. The frequency bandwidth ranges from \(5\) to \(65\) \(\mathrm{Hz}\). The length of time-domain signal is 6 \(\mathrm{s}\) and is sampled at 0.004 \(\mathrm{s}\). The source-signature is a Ricker wavelet with a central frequency of \(25\,\mathrm{Hz}\).

To mimic a simultaneous land experiment, we use four vibrators separated by \(250\,\mathrm{m}\). Figure 2 shows the sweep signatures for the four segments, which we use in different combinations to generate simultaneous sources as shown in the rows of Figure 1 . Once we record all four simultaneous sources at fixed stations (Figure 1), we move the vibrators by 25 m to the next station. Since the aim is to increase the productivity of the phase- and frequency-encoding scheme, we randomly select 50% of the simultaneous sweeps sequences (rows in Figure 2). Note that, with 50% subsampling of the sweep combinations, the total listening time becomes 22 s at each of the four fixed stations compared to 104 s of conventional sequential acquisition time, thus reducing the sweeping time by a factor of \(\approx 5\).

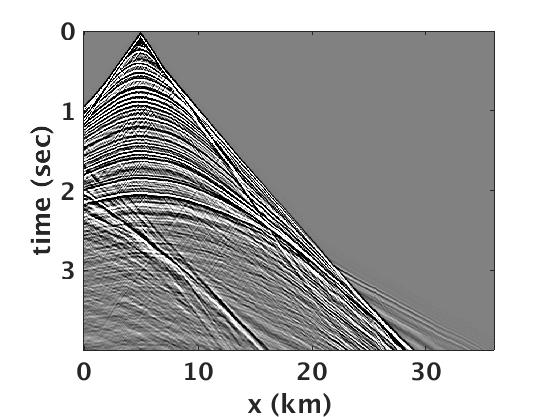
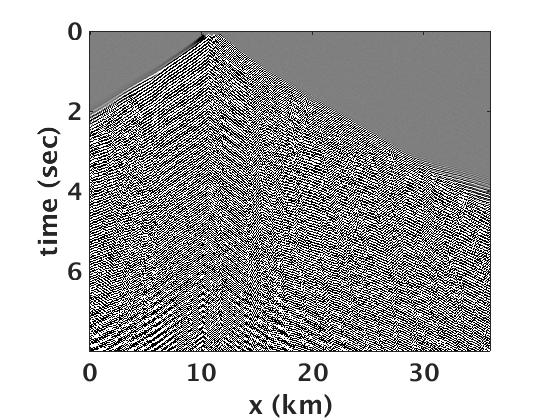
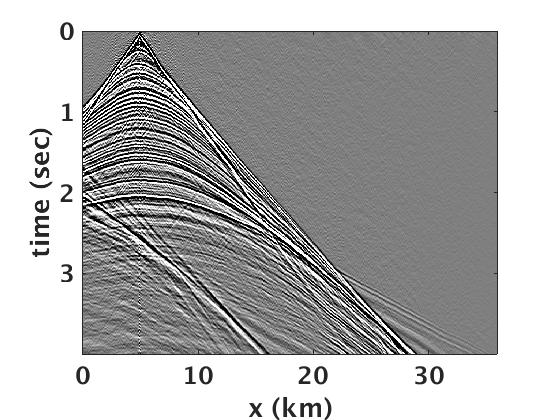
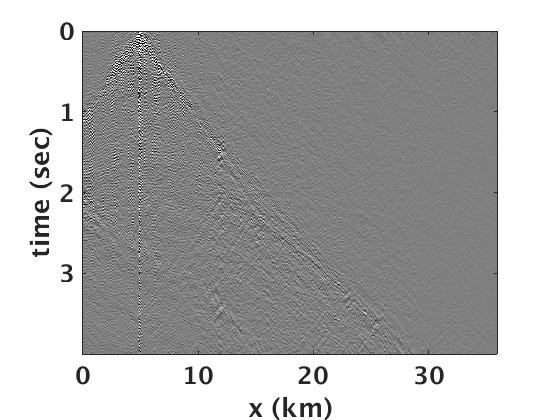
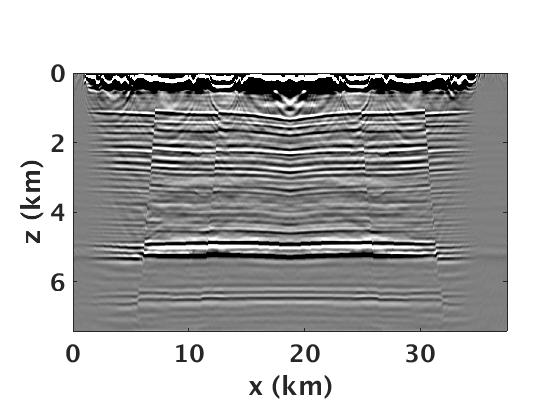
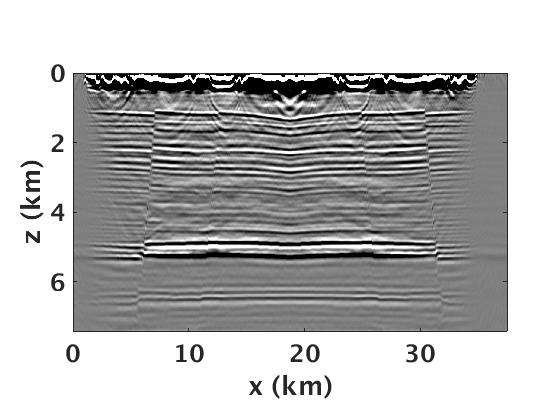
To reconstruct the full bandwidth deblended Green’s function, we run SPGLR framework (Aravkin et al. (2014)), which was specifically designed to solve equation \(\ref{BPDNnuc}\) for large-scale seismic data. Figure 3 a shows the true Green’s function, which we use as a benchmark to compare the reconstructed Green’s function. Figure 3 b includes the blended source gather from one of the sweep combinations. We then perform the rank-minimization based joint source separation and spectral interpolation to reconstruct the full bandwidth Green’s function. The separated and interpolated common receiver gather is shown in Figure 3 c and the corresponding residual with respect to the true Green’s function is plotted in Figure 3 d. We can clearly see that we are able to recover the coherent seismic events like reflection, refractions, diffraction and strong nearly vertical events generated from complex near-surface topology. We further perform the time-domain reverse-time migration (Louboutin et al. (2018)) on deblended and interpolated Green’s function and compare it with the true Green’s function (Figure 4). It is quite evident that the suggested rank-minimization based separation and interpolation technique preserve the continuity of both the reflectors and the Faults in shallow and deeper parts of the model.

Discussions

In this work, we did not address the ground roll and the statics, that are typical challenges for land data processing, as our focus was on application of compressive sensing for simultaneous acquisition with encoded sweeps. The synthetic data created was based on the SEG SEAM-II acoustic model. We plan to simulate data with elastic modeling that will require P, S and density SEAM-II models. Also, we are working on a field dataset acquired with simultaneous encoded sweeps where ground roll attenuation and static corrections were addressed (Moldoveanu et al. (2017)).

Conclusions

We presented a way to increase productivity of land simultaneous shooting method by randomly subsampling the sweep sequences in the phase- and frequency-encoding scheme. The proposed acquisition design substantially reduce the sweeping time and is beneficial for areas where large number of vibrators are not available. Since the randomly selected sweep sequences generate large gaps in the frequency spectrum, we also implemented a computationally efficient rank-minimization based joint source separation and spectral interpolation framework to reconstruct the fully sampled Green’s function. We illustrated with examples that we can gain a factor of \(\approx 5\) (for 50% subsampling scenario) in acquisition time compared to conventional sequential acquisition. Apart from selecting random sweep sequences, we can also make the source grid coarser, but randomly distributed, which will further cut down the acquisition time substantially. We will present the results of that in future on real 3D land seismic data acquired in West Texas.

Acknowledgements

This research was carried out as part of the SINBAD II project with the support of the member organizations of the SINBAD Consortium.