Automatic statics and residual statics correction with low-rank approximation

Introduction

The Earth’s near-surface is usually composed of weathered loose material characterized by a low velocity layer, usually \(250\) to \(1000\) m/s, can be heterogeneous, rapidly changing and season dependent (Sheriff and Geldart, 1995). Due to the low velocity of the weathering layer and due to its laterally varying nature, seismic data gets affected by static time shifts. In addition to statics, random and coherent noise is created by the presence of near-surface scatterers, which adds to the problem by masking events of interest making it difficult to obtain a good quality image as we show latter on. This made statics correction an important research topic for decades leading to the development of several statics correction solutions. In this work, we consider two specific types of statics: (i) long wavelength statics generated by the lateral variations in the weathering layer (O. Yilmaz, 2001) and (ii) short wavelength statics (residual statics). Correction for long wavelength statics is usually model-based where a model of the near-surface is first estimated to compute static time shifts, which are then corrected for by applying them on the data. This category includes methods such as uphole surveys, refraction traveltime tomography (Zhu et al., 1992), waveform tomography (Sheng et al., 2006), multi-physics inversion (Colombo et al., 2010), and image-based modeling (Oz Yilmaz, 2013). These methods have provided successful solutions for statics correction. However, they can be cost and time consuming. Also they may lead to unsatisfactory results when certain assumptions are not met such as when events cannot be picked or when the transition between the near-surface and the bedrock is not a distinct one, which can be the case for traveltime tomography and image-based modeling statics correction. When the estimated models contain errors, some static shifts will remain uncorrected for. Additionally, the long-wavelength static correction methods do not account for rapid changes in elevation, base of weathering and weathering velocity (O. Yilmaz, 2001). Therefore correction for short-wavelength residual statics becomes necessary. Residual statics correction is commonly performed in an iterative fashion to improve picking of the normal moveout (NMO) velocity and the residual statics estimation in a flip-flop mode (O. Yilmaz, 2001). Methods in this category include stack power maximization (Ronen and Claerbout, 1985) and linear inversion (Wiggins et al., 1976). These methods assume that residual statics is surface consistent and fail when it is not the case.

Low-rank approximation and rank minimization has been widely used in different applications such as eigenimage processing (Ulrych et al., 1988), interpolation (Kumar et al., 2015; Alfaraj et al., 2017) and denoising (Trickett and Burroughs, 2009). Using similar ideas, we propose an efficient, data-driven and automatic low-rank approximation-based statics and residual statics correction method that automatically corrects for static shifts such that the data becomes low rank in a certain domain without the necessity of computing the actual time shifts, hence the term automatic.

Low-rank approximation

Our proposed method utilizes the fact that static time shifts break the continuity and increase the rank of seismic data, while data without statics can be represented by a low rank in a transform domain. Low rank representation indicates that the data can be approximated by a small number of singular vectors associated with relatively few largest singular values. We chose the midpoint-offset domain to be our transform domain as it preserves the above property and we apply the method on frequency slices. In order to well approximate the midpoint-offset slices by a smaller rank, we propose applying NMO correction on the common midpoints (CMPs), (Trickett and Burroughs, 2009). The NMO velocity that is used for the NMO correction does not need to be very accurate as the method is robust to NMO velocity errors up to a certain limit. We then preform low-rank approximation.

Given a matrix \(\mathbf{X} \in \mathbb{C}^{m \times n}\) that represent a midpoint-offset frequency slice, we perform singular value decomposition (SVD): \[ \begin{equation} \mathbf{X} = \mathbf{U} \mathbf{S} \mathbf{V}^H , \label{eq:svd} \end{equation} \] where (\(^H\)) denotes the Hermitian transpose, \(\mathbf{U} \in \mathbb{C}^{m \times k}\), \(\mathbf{V} \in \mathbb{C}^{n \times k}\) and \(\mathbf{S} \in \mathbb{R}^{k \times k}\) are the matrices holding the left singular vectors, the right singular vectors and the non-negative real-valued singular values of \(\mathbf{X}\), respectively. We select a small number of the singular vectors corresponding to the few largest singular values and obtain a new estimate of \(\mathbf{X}\) that is of lower rank. We should note that performing singular value decomposition is expensive for extremely large matrices. However for our problem, the computational costs are acceptable since we only need to perform the SVD once. This still makes the method computationally efficient. Variations of SVD such as randomized SVD and other rank minimization techniques can be used to speedup the algorithm when having to deal with extremely large matrices.

Numerical results and discussion

We demonstrate the performance of our proposed method on three synthetic data examples: (i) data with random time shifts and reflection events that diverge from the hyperbolic assumption (Figure 1a), (ii) data modeled on a horizontally layered model with a heterogeneous near-surface (Figure 2a), and (iii) data modeled on a more complicated subsurface model with a heterogeneous near-surface (Figure 3a). On all of the examples, we model data with a maximum frequency of \(75\) Hz and with \(10\) m source and receiver intervals. To generate data for example (i), we model statics-free data and randomly shift each trace of each shot and receiver gather by up to \(\pm 40 \) ms. We should note that each trace is shifted by a different amount of time to violate the surface consistency assumption. We roughly estimate an NMO velocity model for NMO correction. We apply our proposed statics correction with low-rank approximation to obtain CMPs with statics-correction applied automatically that we use to stack the data (Figures 1c and 1f).

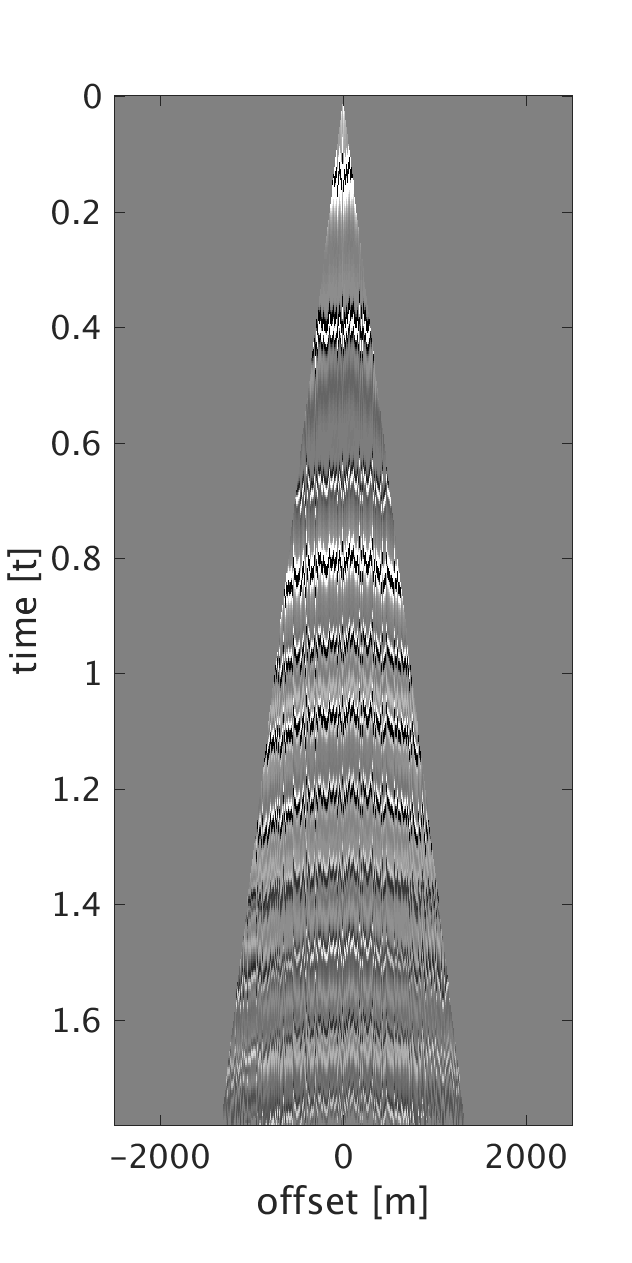
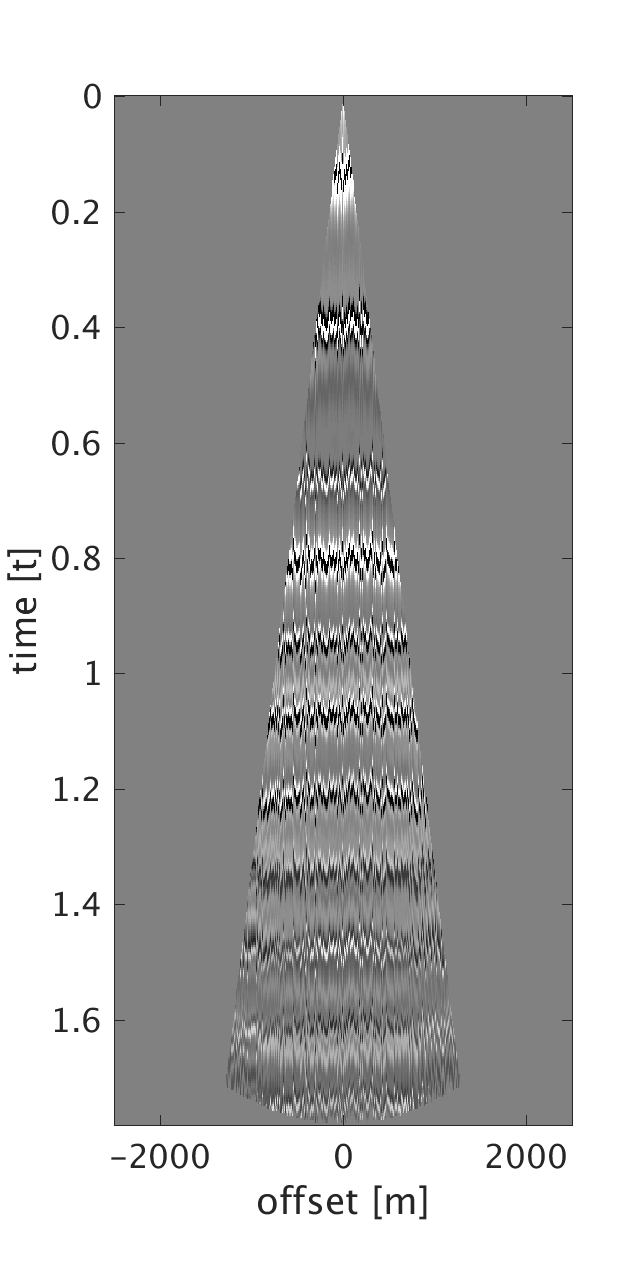
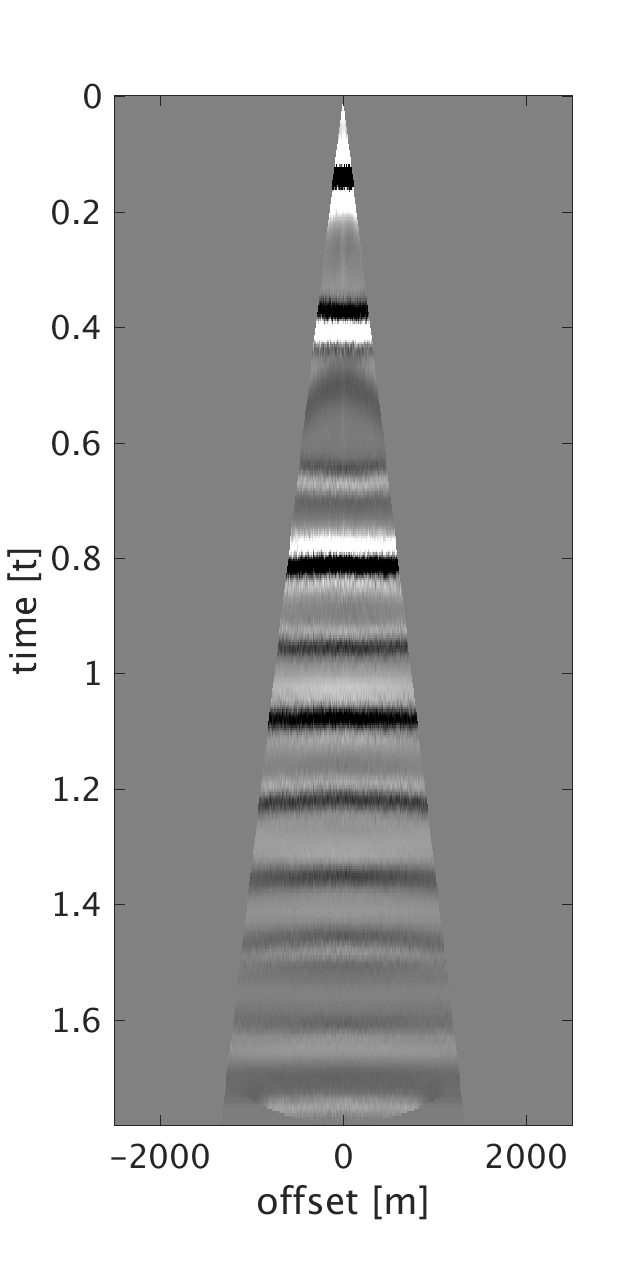
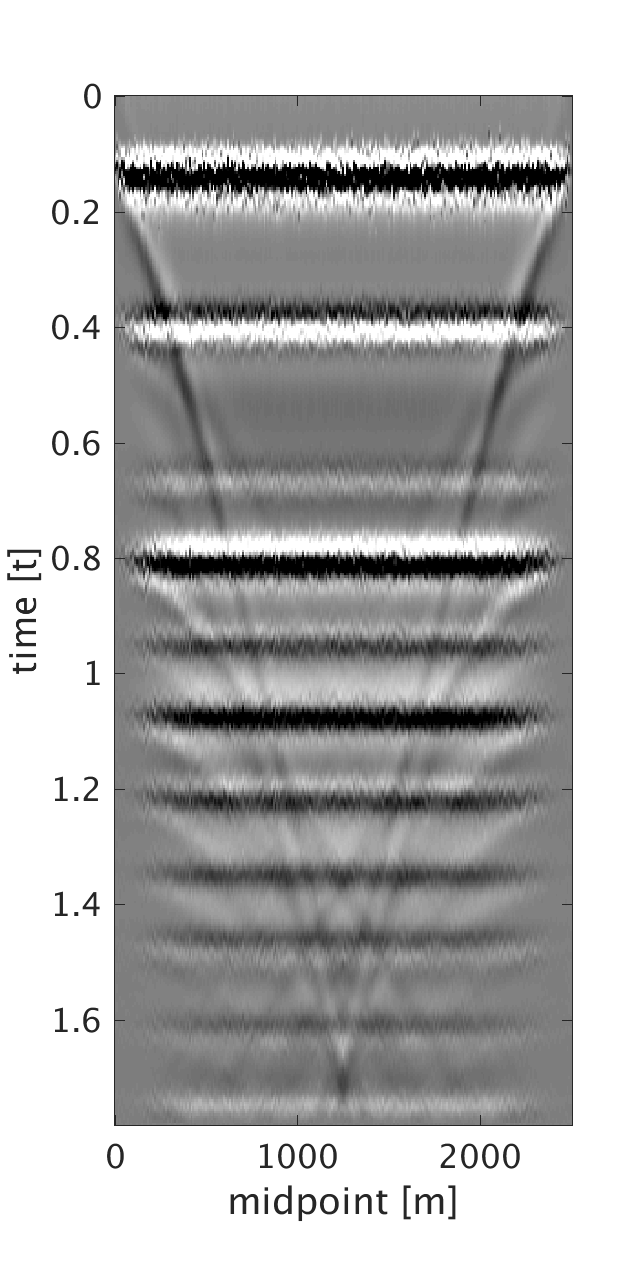
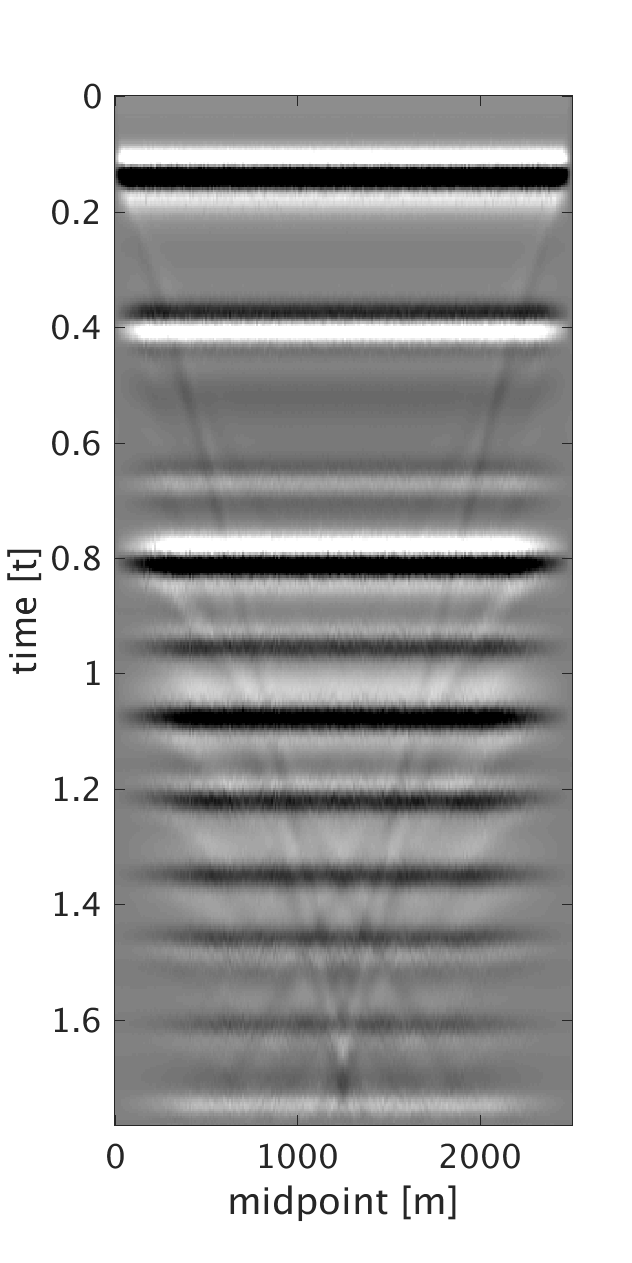
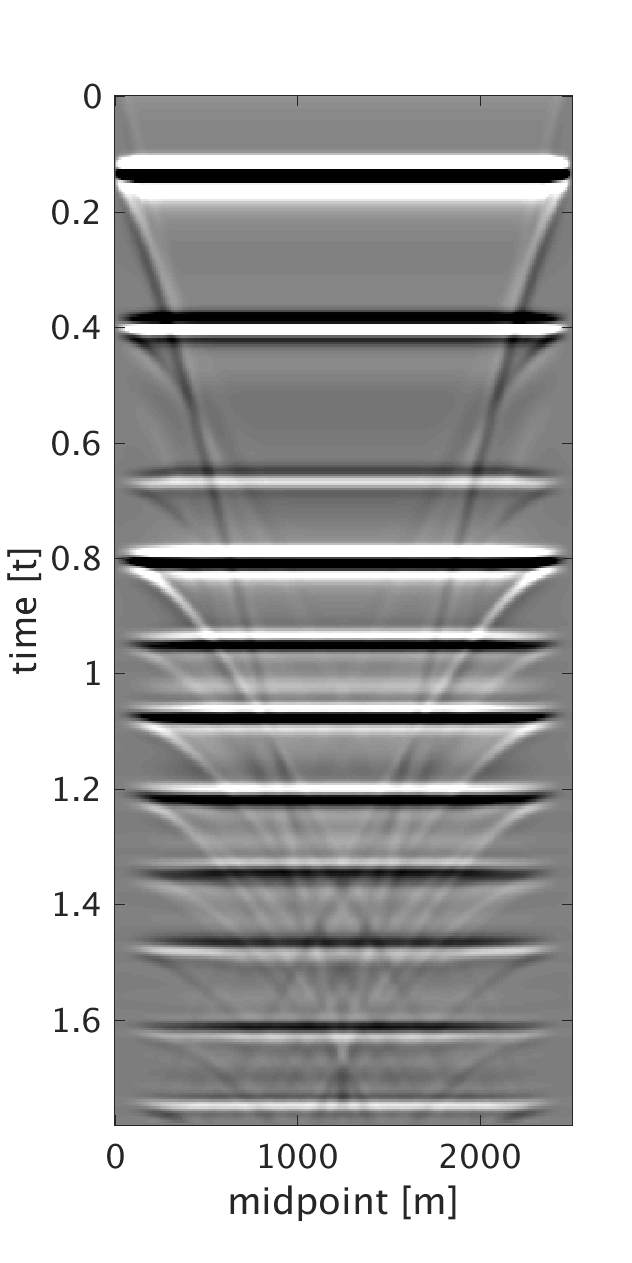
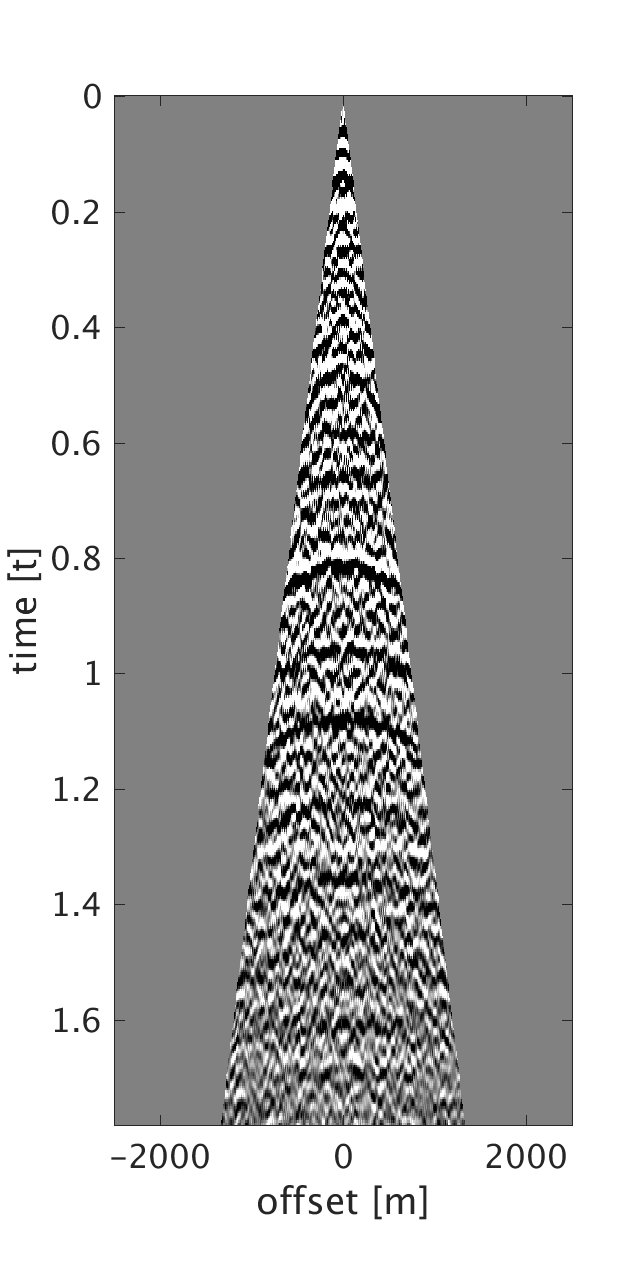
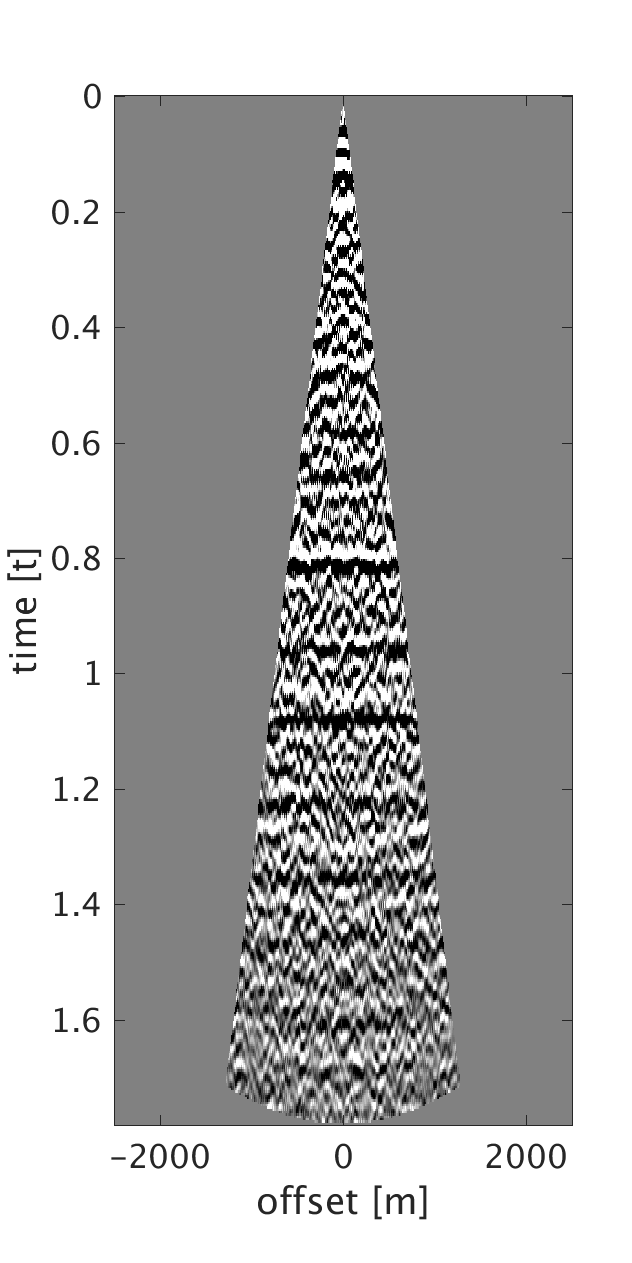
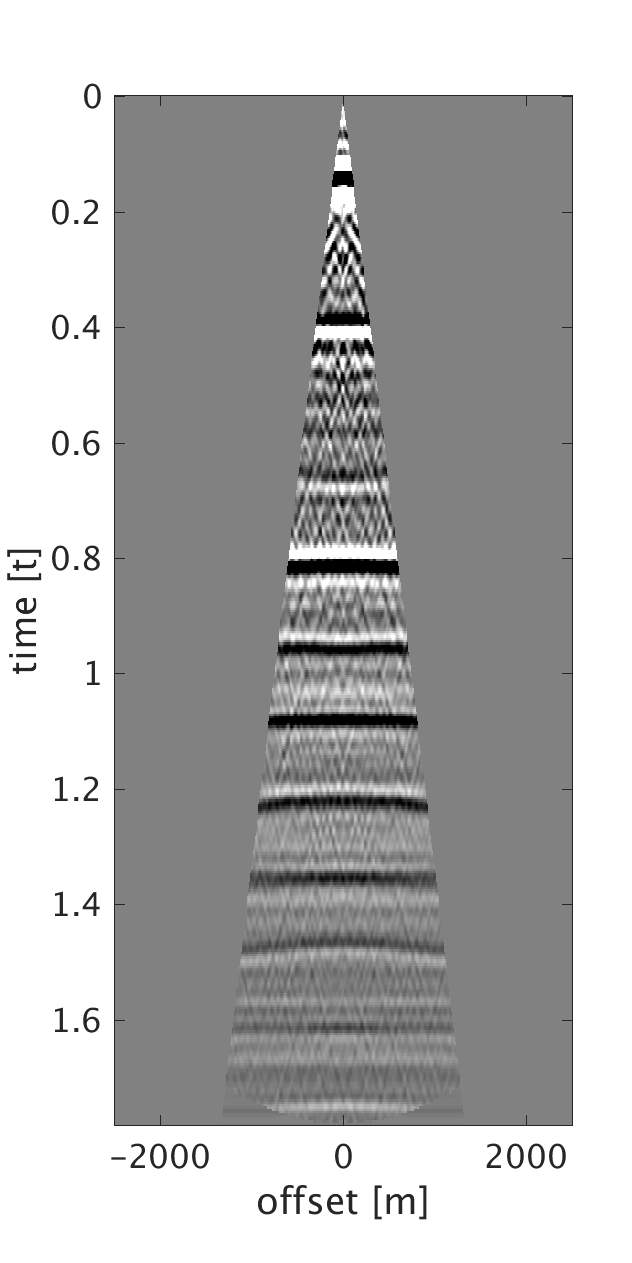
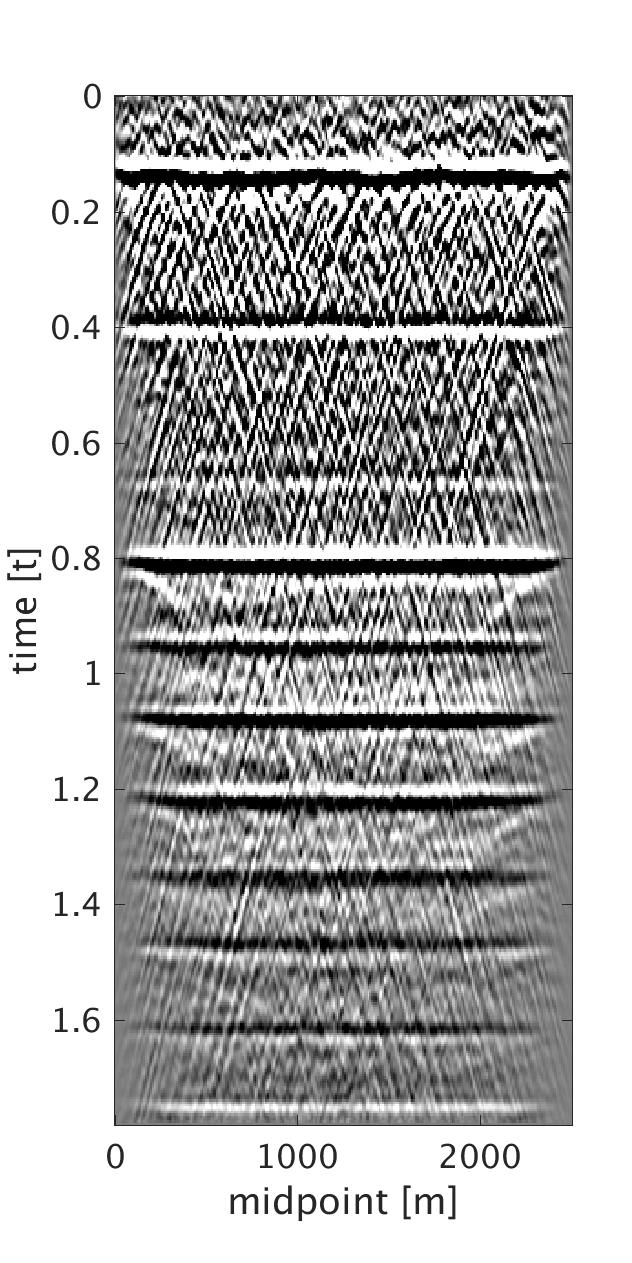
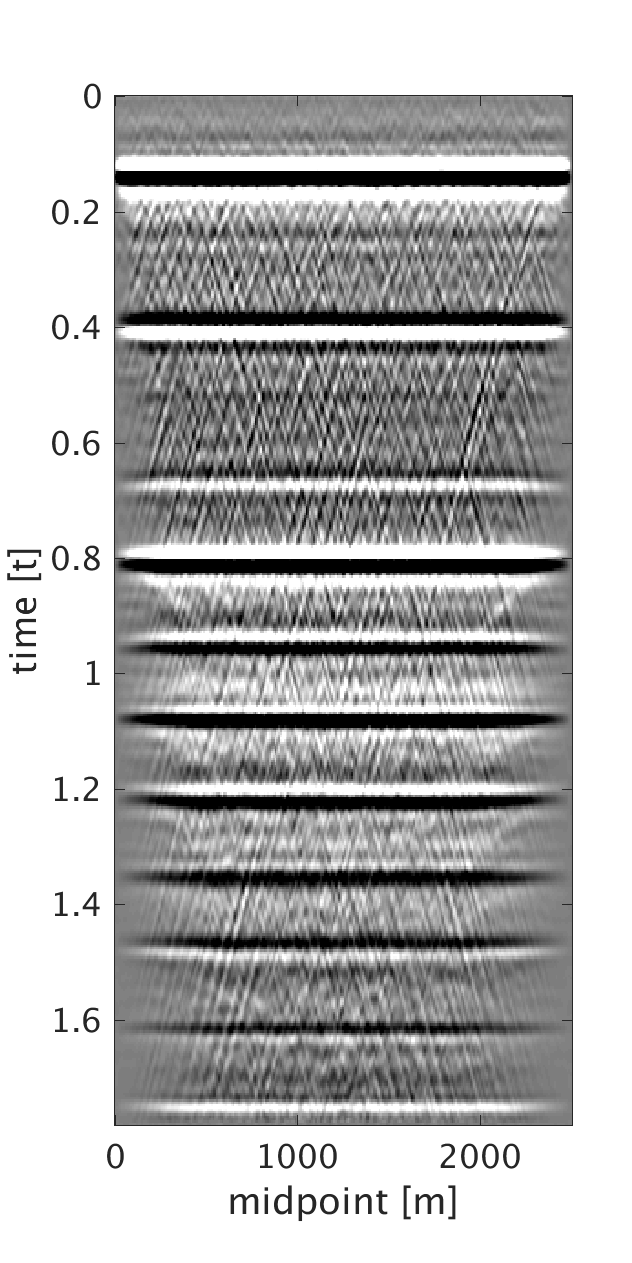
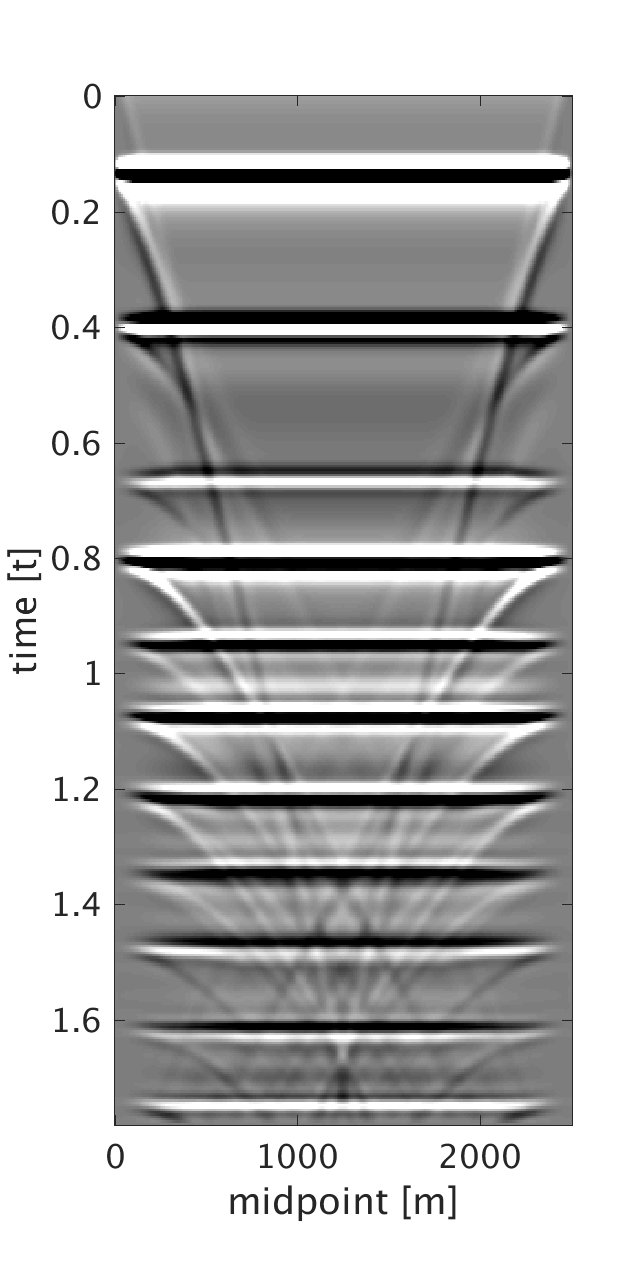
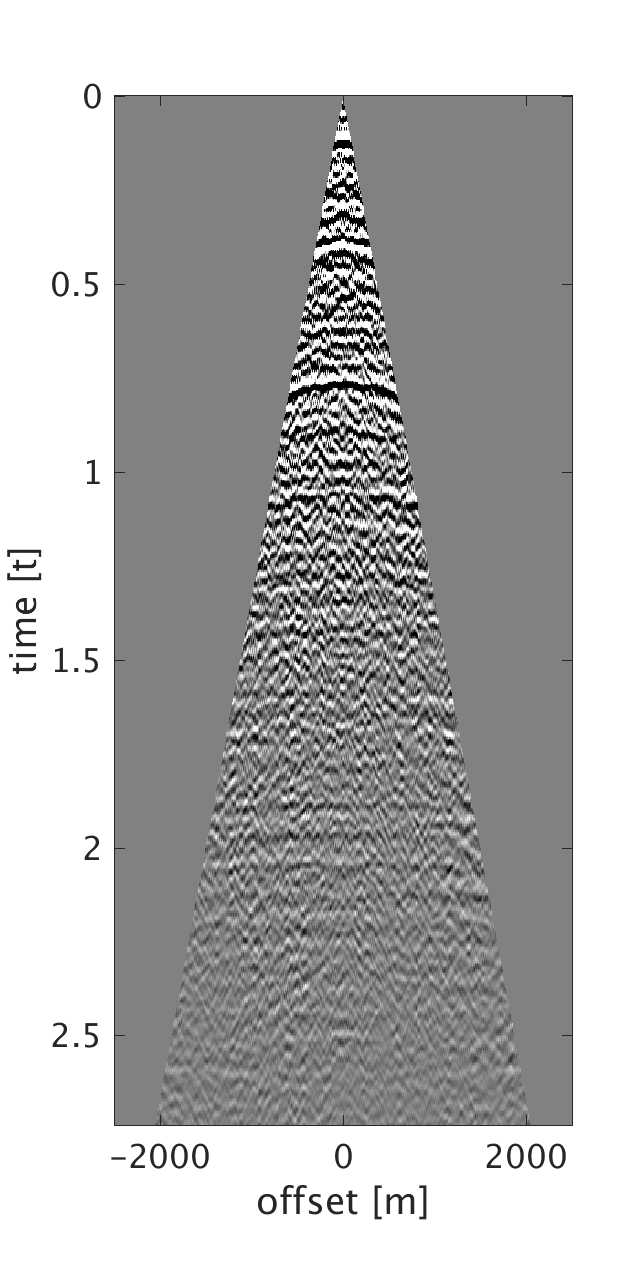
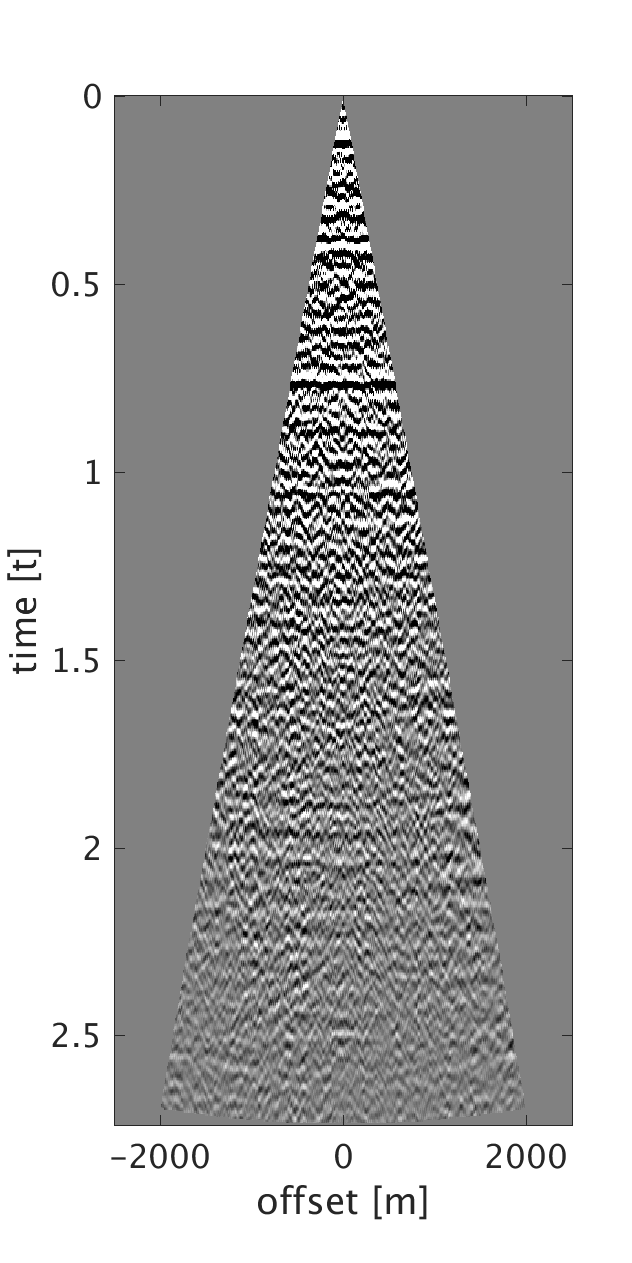
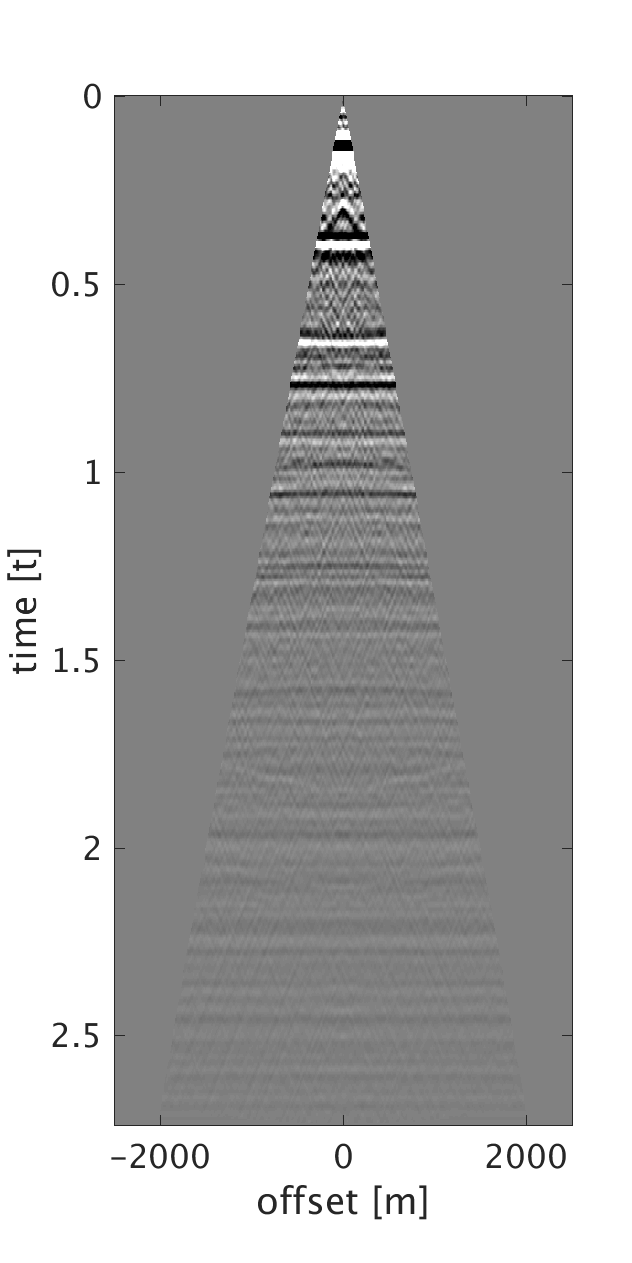
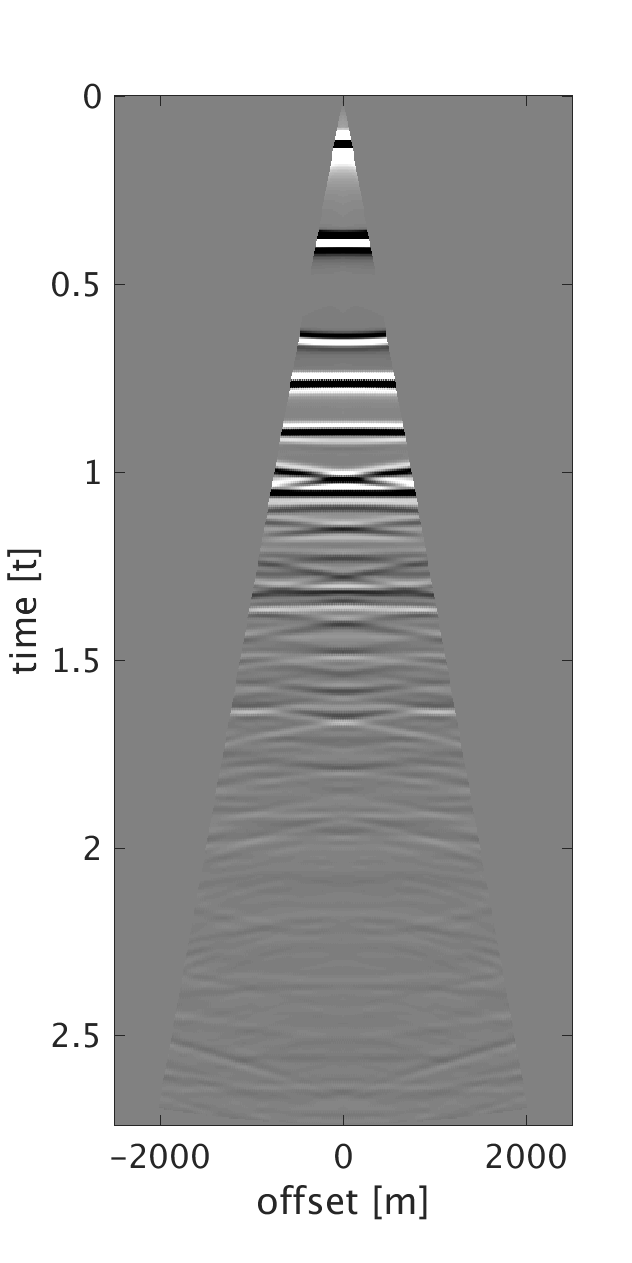
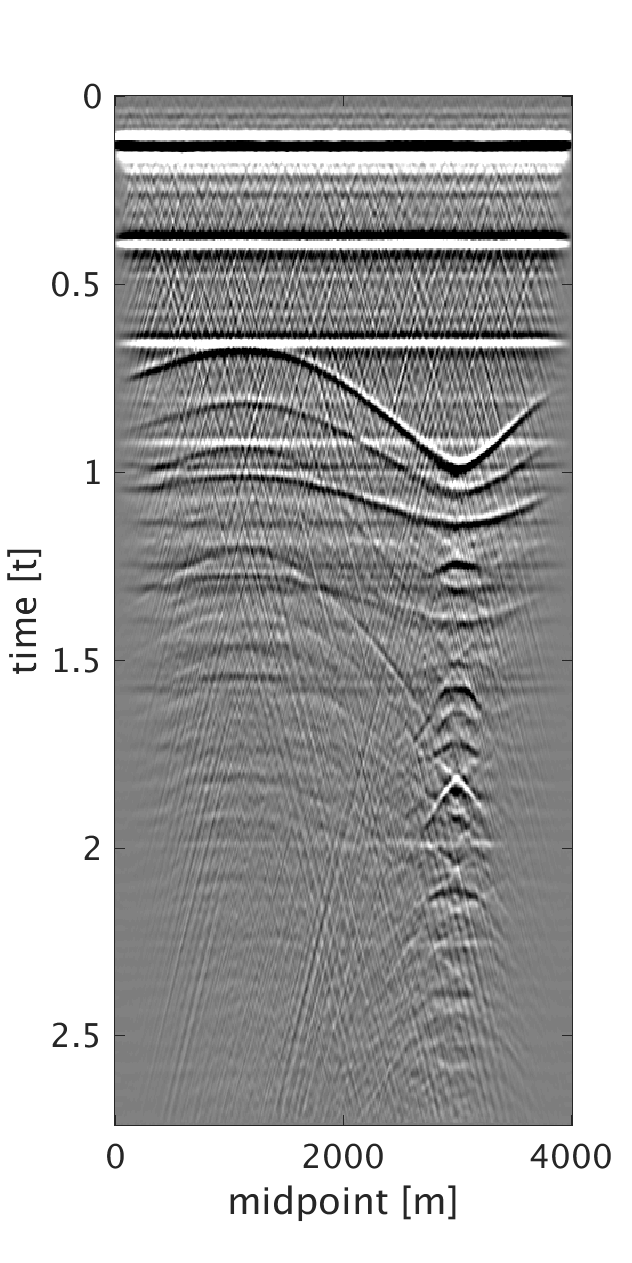
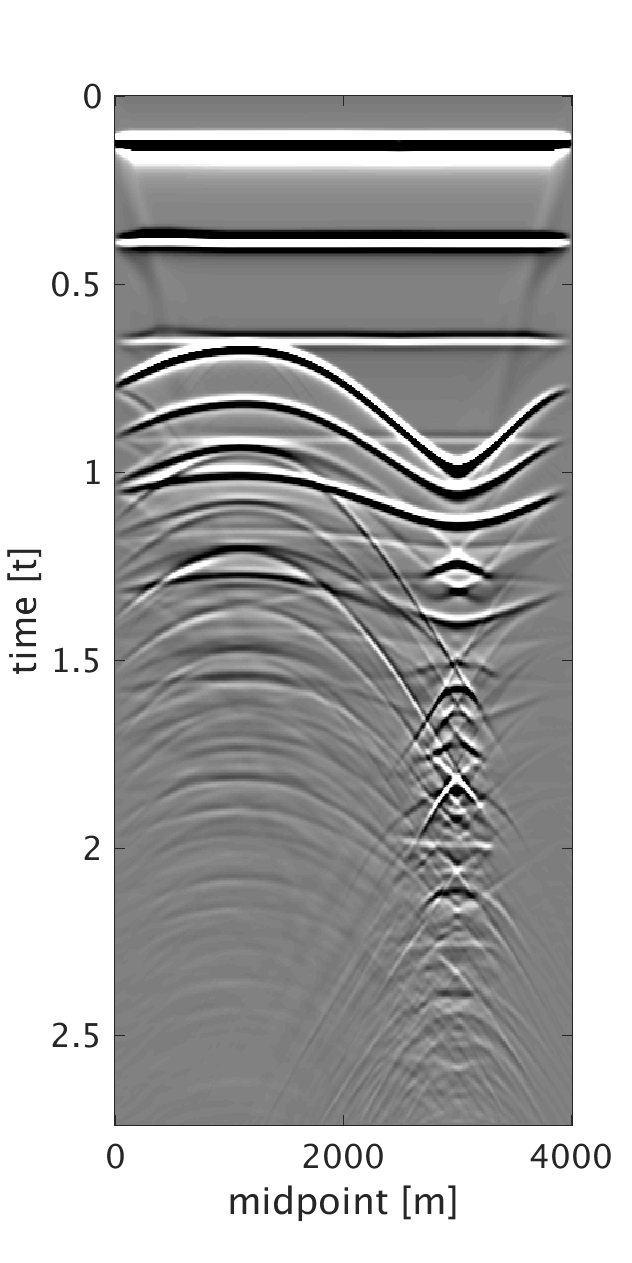
To generate example (ii) data, we replace the first \(200\) m of the first layer of the model we used in example (i) with a rapidly changing, heterogeneous, scattering and low-velocity layer such that it reflects complexity of the near-surface. This results in static shifts and strong noise that masks the events of interest as can be seen from the CMPs on Figures 2a and 2b . We implement our proposed method to obtain CMPs without statics that we use to stack the data (Figures 2c and 2f ). In example (iii), we use a similar near-surface model to the one used in example (ii) but with more complicated subsurface structures. We perform statics correction with low-rank approximation to recover CMPs with statics correction applied and use them to stack the data (Figures 3c and 3f ).

In all of the three examples, we were able to automatically correct for statics using our proposed statics correction with low-rank approximation method. Additional benefits of the method include artifacts and noise suppression as can be seen from examples (ii-iii).

Conclusions

We proposed a data-driven, efficient and automatic statics correction with ow-rank approximation method that corrects for statics by imposing low rank on frequency slices in the midpoint-offset domain. The method can handle data with long wavelength statics resulted from the heterogeneity, scattering nature and low velocity of the near-surface weathering layer. The method can also correct of short wavelength residual statics without the need to the surface consistency assumption. As of now, our proposed method is applicable to data that has elevation statics applied to it. We demonstrated the successful application of our method on several synthetic data examples and on the process of applying it to real data.

Acknowledgements

Ali Alfaraj extends his gratitude to Saudi Aramco for sponsoring his Ph.D. studies at the University of British Columbia. We would like to thank Andrey Bakulin and Ilya Silvestrov for the fruitful discussions and for providing the near-surface model. This research was carried out as part of the SINBAD project with the support of the member organizations of the SINBAD Consortium.