Denoising high-amplitude cross-flow noise using curvelet-based stable principle component pursuit

Introduction

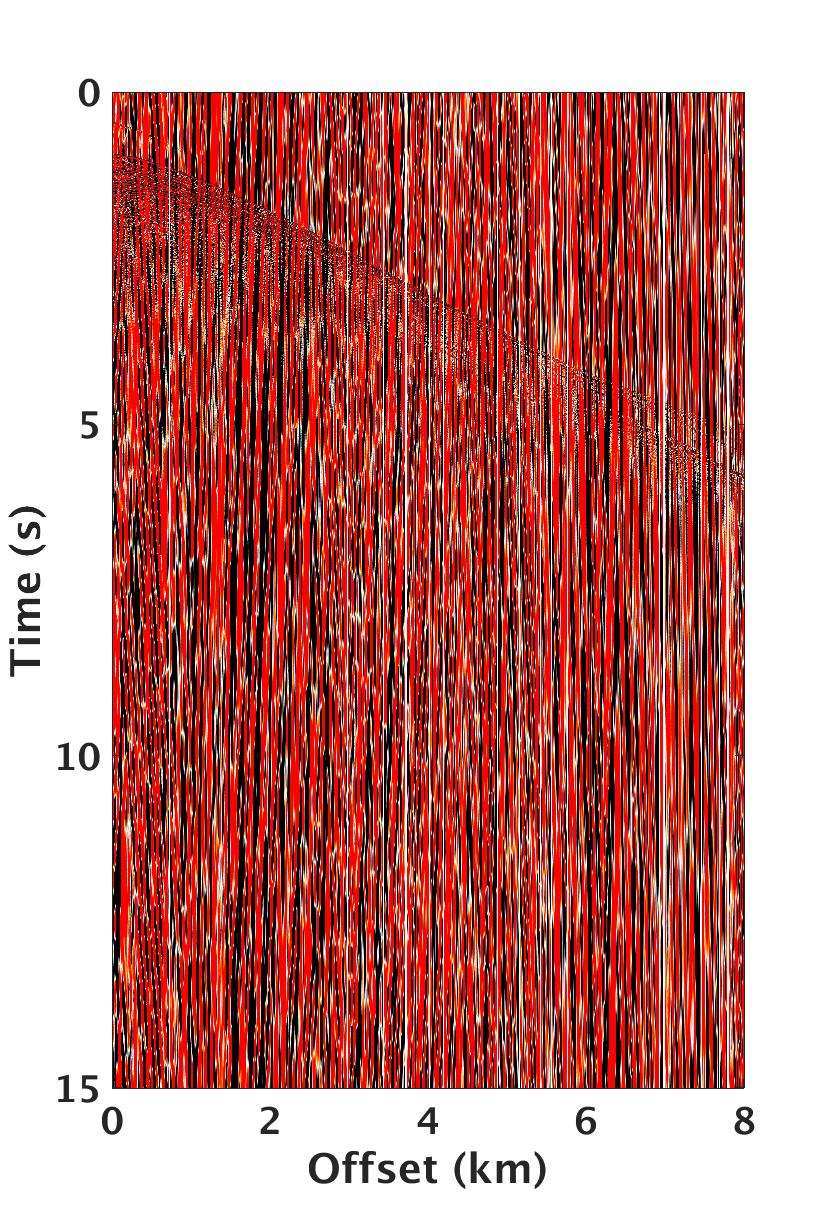
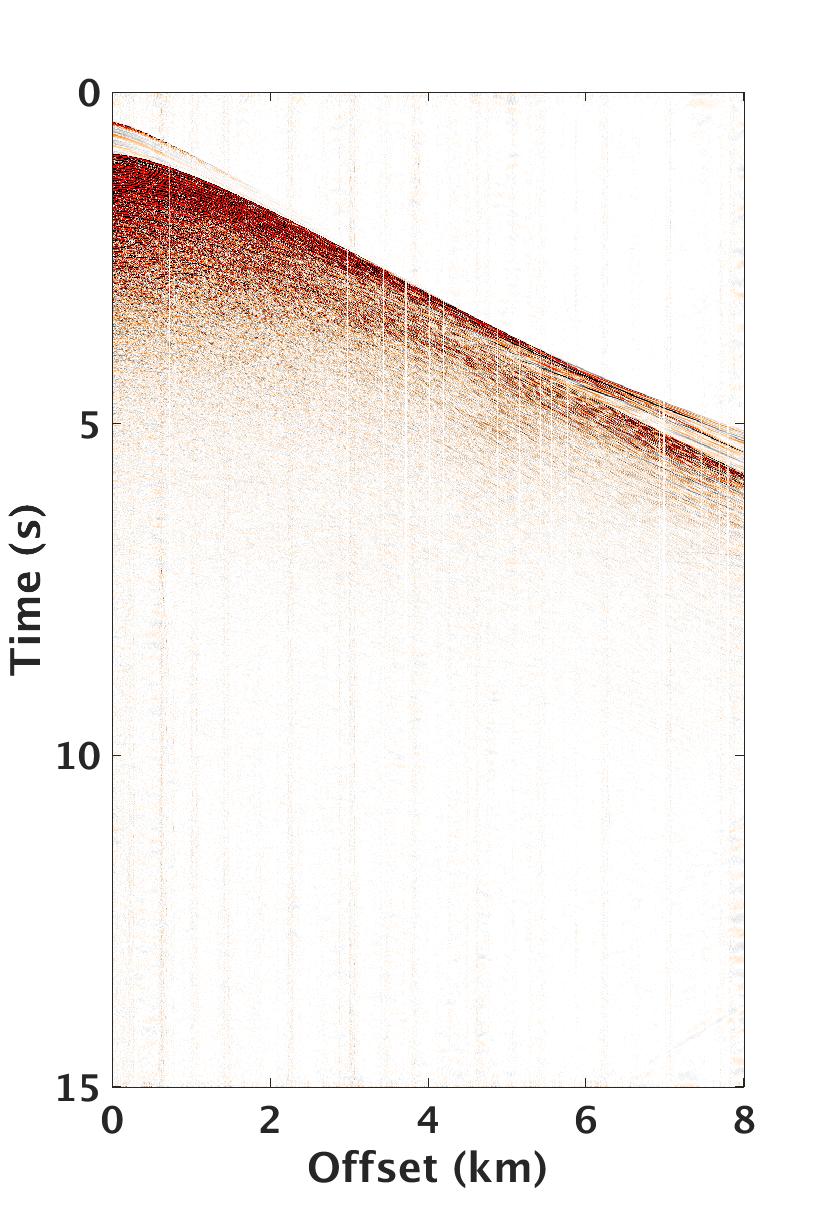
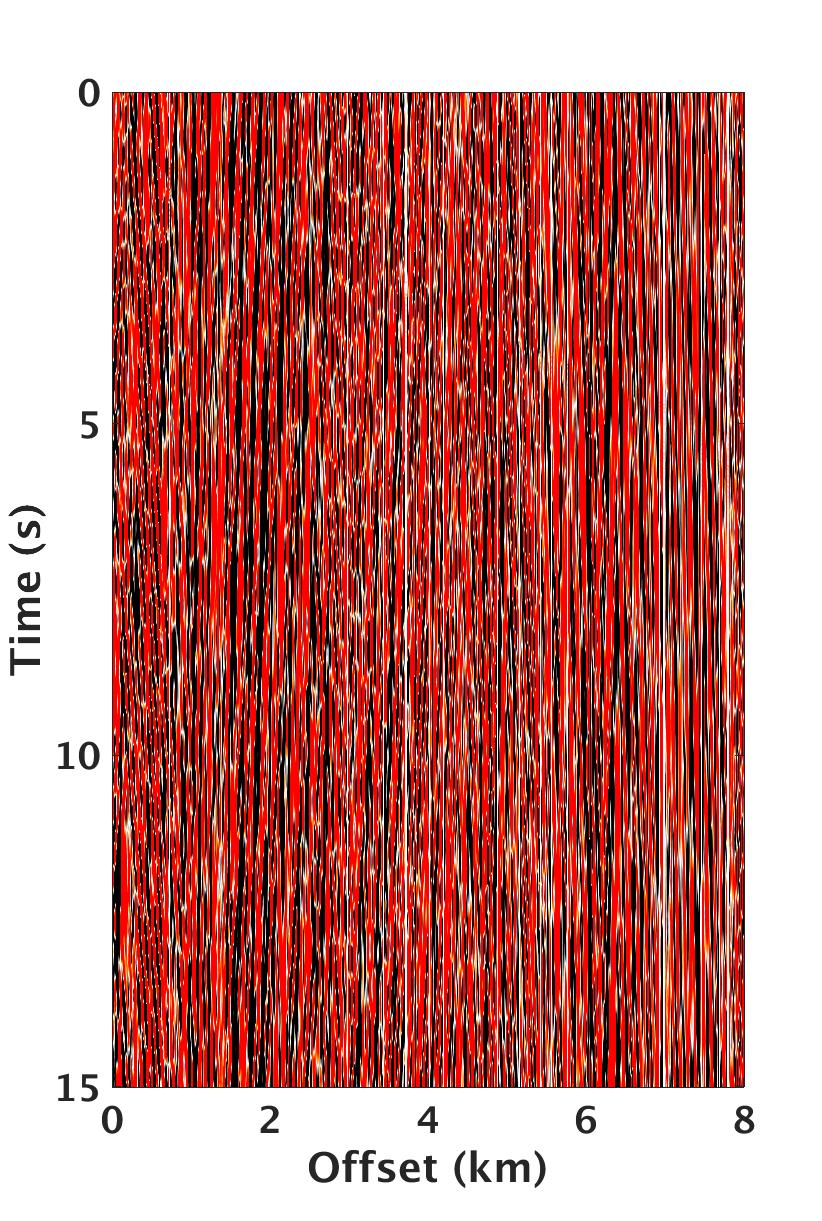
Cross-flow of water across the streamers often results in high-amplitude steeply dipping low-frequency noise that overlay the seismic signal of interest. Moldoveanu (2011) showed that for coil shooting, cross-flow noise at low-frequencies (0 to 5 Hz) can be as high as 30 dB with respect to the seismic signal and comparable in energy to the diving waves and seismic reflectivity within 5 to 10 Hz frequency range. Contamination at the low-frequencies of the seismic signal can adversely affect full-waveform inversion and imaging workflows that rely on these frequencies to resolve deep targets of interest. We included Figure 1 to display a common-shot gather extracted from a coil survey where the high-amplitude cross-flow noise overlays the relatively low-amplitude part of the seismic signal. Moldoveanu (2011) showed that the cross-flow noise is low-rank, i.e., cross-flow noise can be approximated by singular vectors that correspond to the first few largest singular values, which can be computed from noisy coil data when organized as a matrix in the time-space domain.

Moldoveanu (2011) exploited this low-rank property by deriving an iterative that consists of the following steps: (i) estimation of the cross-flow noise with a singular-value decomposition consisting of the few largest singular values; (ii) subtraction of this estimate for the cross-flow noise from the noisy input data; (iii) repeat step (i) and (ii) for a fixed number of user defined iterations; (iv) perform LACONA (Özbek, 2000; Martin et al., 2000) to suppress the remanent noise in the shot gathers. While this method has been utilized with success, it is only applied in a relatively small frequency band (0-5 Hz or 0-10 Hz), where noise dominates the signal. As a result, this iterative process may leave residual flow noise at higher frequencies that may be harmful because it can affect the resolution and continuity of the geological features like reflectors and faults in imaging workflows. To overcome residual flow noise at higher frequencies where this noise is more difficult to separate from diving waves and reflection events, we propose a method that exploits the fact that the curvelet transform compresses seismic data, which allows for a separation of incoherent noise and signal (Neelamani et al., 2008; Herrmann et al., 2013). We built on this property of curvelets to separate flow noise from turning waves and broadband reflection data with minimal impact. Contrary to purely sparsity-based methods, which often rely on many forward and inverse curvelet transforms, we opt to separate the flow noise from the diving waves and reflection data decomposing the curvelet coefficients, which live for each scale in angular wedges, into sparse and low-rank components with the recently developed stable principle component pursuit (SPCP) approach. The abstract is organized as follows. First, we motivate the use of curvelet transform as a domain to separate flow noise from diving waves and reflection events collected in coil data. Next, we derive a version of SPCP that allows us to separate noise that permits low-rank approximations across different scales and angles in the curvelet domain. Finally, we demonstrate the performance of our method on a real shot record taken from coil shooting survey acquired in the Gulf of Mexico.

Curvelet-based SPCP

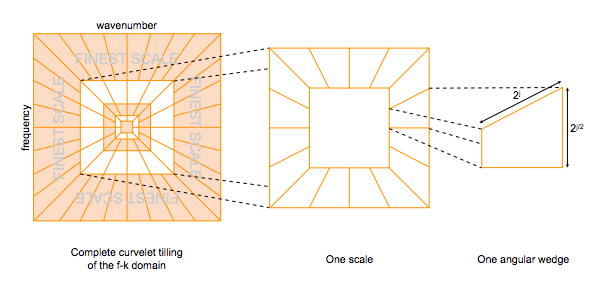
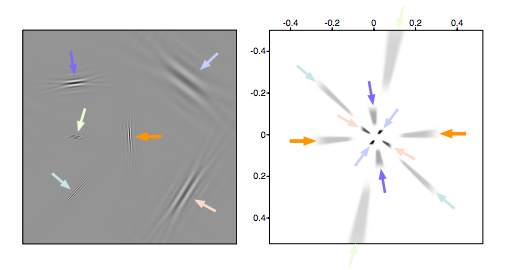
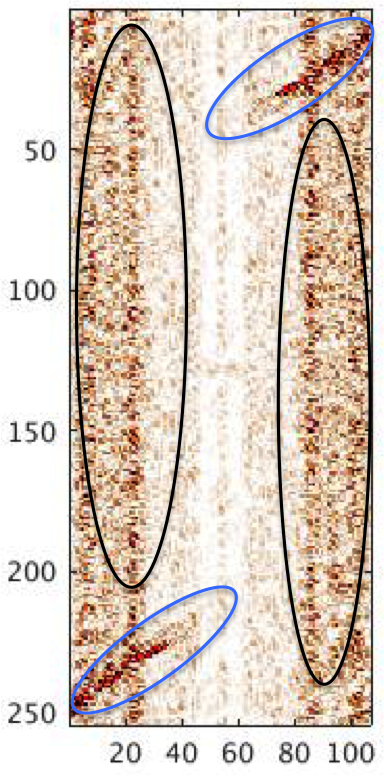
For coil shooting surveys, cross-flow noise completely dominates seismic data in the low-frequency band (0-5 Hz) and is comparable in amplitude to diving waves and reflection data in the 5-10 Hz frequency band. This property makes the removal of cross-flow noise while preserving the amplitudes of diving waves and reflection events challenging. As shown in Figure 2, the curvelet transform decomposes seismic data into multiscale and multi-angular wedges in 2D Fourier domain (Candes and Donoho, 2000). As a result of this construction, curvelets are able to separate signal components based on their location, scale, and dip explaining its succesful application in both incoherent (Neelamani et al., 2008; Herrmann et al., 2013) and coherent (Lin and Herrmann, 2013) seismic signal separation. For seismic data with flow noise, we find as shown in Figure 3 that the seismic events and coherent flow noise map across different scales to different locations in the angular wedges (juxtapose events encircled by black and blue denoting curvelet coefficients associated with flow noise and seismic events, respectively). The fact that the flow noise is predominantly vertically oriented suggests an underlying low-rank structure as opposed to the seismic events, which are localized along filament structures that have curvature. This difference in morphological appearance suggests a possible separation scheme between the low-rank flow noise related coefficients and the sparse curvelet coefficients that are associated with the diving waves and reflection events.

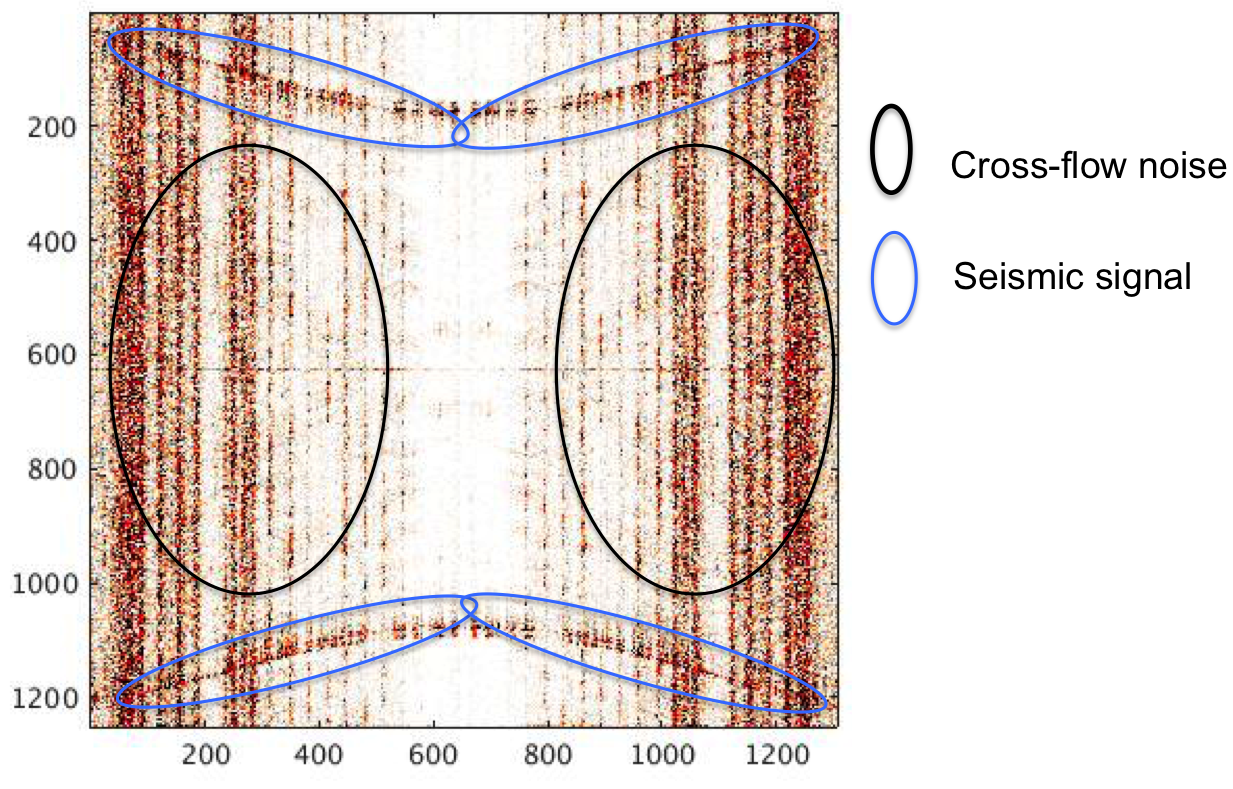
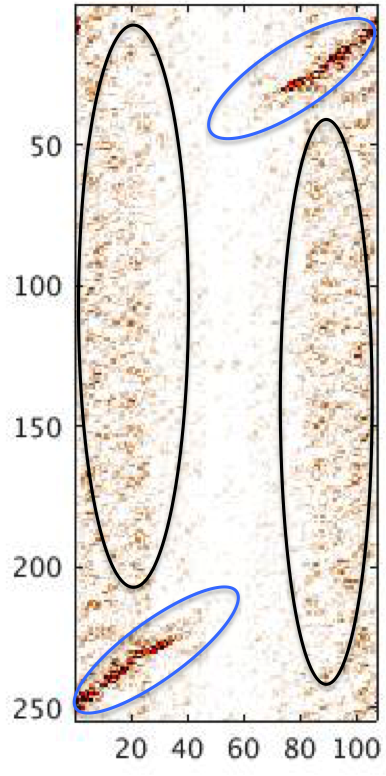
To separate the low-rank cross-flow noise from the sparse curvelet coefficients associated with the reflection and diving waves, we use the \(\text{SPCP}_{max}\) method proposed by Aravkin et al. (2014), where we decompose the curvelet coefficients (in each angular wedge corresponding to a subset of frequencies and wavenumbers at different scales) organized as matrices \(\mathbf{Y}\) into low-rank cross-flow noise components, denoted by \(\mathbf{L}\), and a sparse components, denoted by \(\mathbf{S}\). Following Aravkin et al. (2014), we separate these components by solving the following convex optimization program: \[ \begin{equation} \minim_{\mathbf{L},\mathbf{S}} \quad \max(\|\mathbf{L}\|_* , \lambda_{max} \|\mathbf{S}\|_1) \quad \text{subject to} \quad \|\mathbf{L}+\mathbf{S} - \mathbf{Y}\|_F \leq \epsilon, \label{SPCPmax} \end{equation} \] where the \(\|.\|_1\) (\(\ell_1\)-norm), \(\|.\|_*\) (the nuclear norm), and \(\|.\|_F\) (the Frobenius norm) are given by \(\|\mathbf{S}\|_1 = \sum_{i,j} |s_{i,j}|, \|\mathbf{L}\|_* = \sum_i \sigma_i(\mathbf{L})\), and \(\|\mathbf{B}\|_F = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^m b_{i,j}}\) . \(\sigma_i(\mathbf{L})\) are the singular values of \(\mathbf{L}\). The parameter \(\lambda_{max}\) controls the relative importance of the low-rank component \(\mathbf{L}\) vs. the sparse component \(\mathbf{S}\), and \(\epsilon\) is the \(\ell_2\) norm of the error in the residual \(\mathbf{Y} - (\mathbf{L} + \mathbf{S})\) not explained by the superposition of \(\mathbf{L}\) and \(\mathbf{S}\).

Our curvelet-based algorithm consists of the following main steps: (i) perform the forward curvelet transform on each shot gather; (ii) extract the noisy curvelet coefficients along parabolic angular wedges at each scale and organize these coefficients into a matrix \(\mathbf{Y}\); (iii) solve SPCP (equation \(\ref{SPCPmax}\)) on each of these matrices independently to separate the low-rank flow noise \(\mathbf{L}\) from the sparse diving waves and reflected component \(\mathbf{S}\); (iv) insert the separated curvelet coefficients for each scale back into the corresponding parabolic angular wedges; (v) perform the inverse curvelet transform to get estimates for shot records for the separated components.

Coil shooting survey—Gulf of Mexico

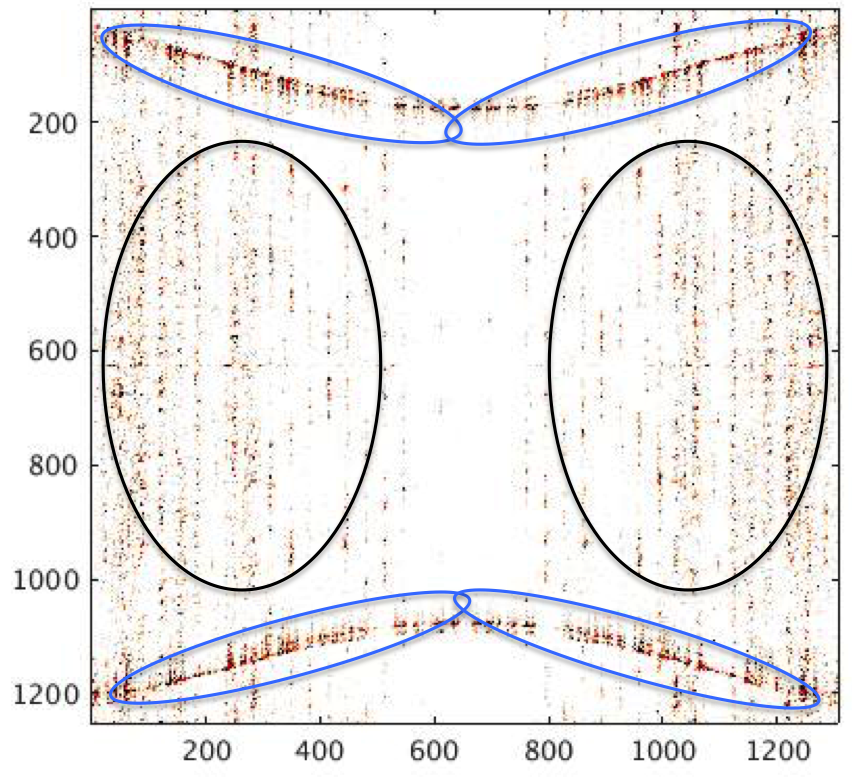
We test the efficacy of our curvelet-based SPCP formulation on a common-shot gather extracted from a coil shooting survey acquired in the Gulf of Mexico. The coil survey used in this study was acquired with an acquisition system that has single sensors (hydrophones) spaced at 3.125 m and without a low-cut acquisition filter applied. These acquisition parameters allow us to perform better signal separation because the data is not aliased due to fine receiver sampling. To choose appropriate \(\lambda_{max}\) and \(\epsilon\) values in equation \(\ref{SPCPmax}\) for all the parabolic wedges at different scales and angles, we perform the signal separation for wedges at the coarsest and finest scale first. Via experimentation, we find that we get the best results for these two cases when the \(\lambda_{max}\)’s and \(\epsilon\) are set to \(0.006\), \(0.9\) and \(1e^{-3}\), respectively. For the intermediate scales, we linearly interpolate the values for the \(\lambda_{max}\)’s from the values we found at the finest and coarsest scales. Figures 3 (c, d) show the separated curvelet coefficients for these parameter settings at the coarsest and finest scales. From this Figure, we can see that the cross-flow noise is well separated without leaking reflected energy and diving waves. The final separated result in the time-space domain is shown in Figure 4 a. This result clearly shows that our curvelet-based SPCP approach can successfully separate high-amplitude low-frequency cross-flow noise (Figures 4 b) from reflection data and diving waves without loosing coherent reflection data and diving waves (see Figure 4 c) as we can see when we apply a low-cut 4 Hz filter on the removed low-rank noisy component (Figures 4 b).

Conclusions

We demonstrate the potential of curvelet-based SPCP approach for separating high-amplitude low-frequency cross-flow noise from the reflected or refracted seismic data on a coil survey from the Gulf of Mexico. We find that the curvelet transform maps the cross-flow noise and seismic signals to low-rank and sparse structures. As a result, we are able to separate these morphologically distinct— the flow noise is low-rank while the seismic events are sparse—signal components with negligible damage to the reflection data and diving waves. Since denoising is performed independently along different scales and angles our curvelet-based SPCP framework can readily be parallelized. As future research, we aim to test the curvelet-based SPCP approach to different types of noise present in the seismic data including ground roll.

Acknowledgements

This research was carried out as part of the SINBAD II project with the support of the member organizations of the SINBAD Consortium. We would like to thanks Stephen Becker and Aleksandr Aravkin for the MATLAB codes used in this work to solve the SPCP formulation.